Numerické řešení rovnice

Ukážeme si, jak je možné numericky vyřešit rovnici. Použijeme funkci fsolve z knihovny scipy. Ukážeme si základní použití a upozorníme na dvě záludnosti.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy import optimize

Vyřešíme rovnici

\[x^2=2.\]

Rovnici je nutné převést tak, aby se hledal nulový bod funkce, tj. do tvaru

\[x^2-2=0.\]

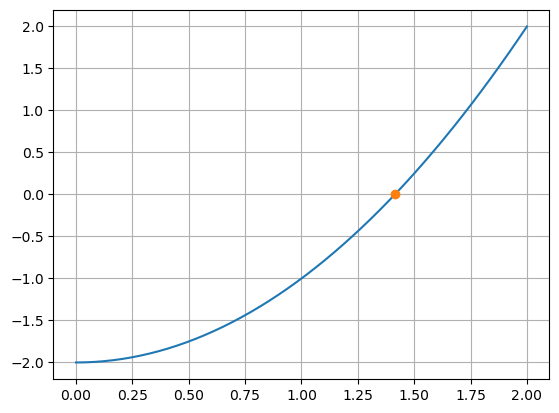
Poté stačí zvolit počáteční odhad řešení a získáme výsledek. Ten je možné zkontrolovat dosazením nebo graficky. Vidíme první záludnost, že ze dvou řešení numerická procedura najde jen jedno, odmocninu ze dvou. Druhé řešení by se dalo najít zvolením počátečního odhadu blízko čísla \(-\sqrt{2}.\)

reseni = optimize.fsolve(lambda x:x**2-2,1)
reseni

array([1.41421356])

reseni**2

array([2.])

x = np.linspace(0,2)
plt.plot(x,x**2-2)
plt.plot(reseni,reseni**2-2,"o")
plt.grid()

Ukážeme si, že může záležet na kvalitě počátečního odhadu řešení. Pokusíme se najít nulové body funkce kosinus. S nulovou výchozí hodnotou výsledek nedopadne dobře. Vyjde nesmírně velké číslo. To proto, že v nule funkce kosinus ani neroste ani neklesá a procedura tak nemá spolehlivé vodítko, jestli nulový bod hledat vlevo nebo vpravo a ani odhad, jak by tento nulový bod mohl být daleko.

reseni1 = optimize.fsolve(lambda x:np.cos(x),0)
reseni1

array([3.79302211e+08])

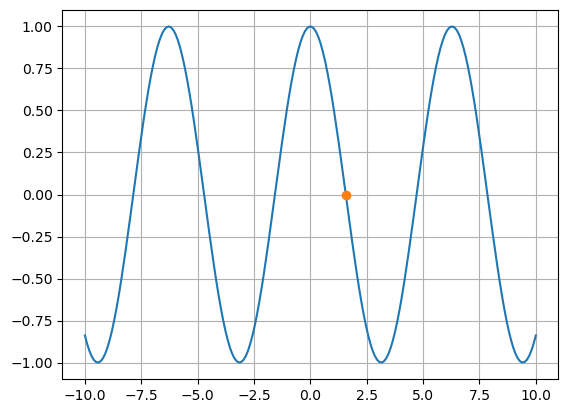
S lepším výchozím odhadem je situace lepší, vyjde nám první nulový bod funkce kosinus, což můžeme zkontrolovat na obrázku.

reseni2 = optimize.fsolve(lambda x:np.cos(x),1)
reseni2

array([1.57079633])

x = np.linspace(-10,10,200)
plt.plot(x,np.cos(x))
plt.plot(reseni2,np.cos(reseni2),"o")
plt.grid()