Ctrl+K

Úvod do jazyka Python

2. Úvod do jazyka Python#

Python patří mezi nástroje pro dávkové zpracování dat. V tomto případě se nepostupuje interaktivně jako například v MS Excel, ale uživatel sestaví posloupnost příkazů a interpreter provede tyto příkazy podobně, jako spuštění programu. Výhody jsou následující.

  • Možnost pracovat s daty neomezené velikosti.

  • Snadná reprodukovatelnost.

  • Lepší přehlednost v rozsáhlejších projektech.

  • Možnost zařazení datové analýzy jako stavebního kamene delšího řetězce.

  • Možnost neomezeného opakování stejné analýzy v cyklu nad jinými daty.

Nevýhoda dávkového zpracování je, že si nemůžeme požadované výstupy zajistit klikáním v menu. Jedná se však o nástroje s širokou uživatelskou základnou a v době kvalitního vyhledávání na Internetu není těžké „vygooglit“ na webech s dotazy a odpověďmi příkazy nutné pro kreslení grafů různých typů a další dílčí úkoly spojené se zpracováním dat. Výhodou jsou mnohem větší možnosti, než má Excel. Srovnatelný se skriptováním v jazyce Python je jedině program Matlab, který je na univerzitě dostupný, ale vzhledem k vysoké ceně nebývá dostupný mimo univerzity a mimo velké firmy.

2.1. Ke způsobu práce#

  • Učíme se na příkladech.

  • Začínáme s modifikací hotových modelů. Experimentujte. Zkoušejte příklady z nápovědy, z přednášek a cvičení.

  • Model stavíme z hotových bloků, málo modelů píšeme od nuly. Často najdeme podobný problém a ten si přizpůsobíme. Například najdeme obrázek podobný našemu zamýšlenému v galerii a odsud vidíme, jaké příkazy a volby je potřeba použít.

  • Detaily k nastavení a volbám při volání funkcí hledáme v manuálu. Pro rychlou orientaci slouží cheatsheety.

  • Spousta dotazů s kvalitními odpověďmi je na serveru StackExchange nebo jinde. Popište hesly problém ve vyhledávacím políčku Google a zkuste vyhledat podobné dotazy a odpovědi na ně. Totéž s chybovými hláškami, pokud jim nerozumíte.

2.2. Co googlit#

Klíčová slova, která se hodí pro dotazy pro vyhledávací službu. Pro potřeby nalezení návodů, tutoriálů, tipů, uživatelského manuálu apod.

Slovo, fráze

Použití

Python

Programovací jazyk, který budeme používat

Jupyter, JupterLab

Prostředí, ve kterém budeme Python používat nejčastěji. Prostředí pro práci je mnoho, volíme takové, které nevyžaduje instalaci na lokální PC.

NumPy

Knihovna numerické výpočty.

SciPy

Knihovna pro řešení diferenciálních rovnic a pro mnoho dalšího.

solve_ivp

Příkaz z knihovny SciPy pro řešení diferenciálních rovnic.

Matplotlib

Knihovna pro kreslení obrázků, grafů. Nejčastěji použijeme pro vizualizaci výstupu přkazu solve_ivp.

Pandas

Knihovna pro práci s tabulkami.

dataframe

Název pro tabulky používaný při práci s knihovnou Pandas.

diferenciální rovnice, počáteční úloha, ODE, ordinary differential equation, IVP, initial value problem

Název matematických nástrojů používaný při modelování

Markdown

Jeden z nejjednodušších značkovacích jazyků, používá se pro doprovodné texty v Jupyter zápisnících

LaTeX, \(\LaTeX\), latex

Nejrychlejší a nejspolehlivější metoda psaní matematických výrazů do textu, kompatibilní s Markdown a s relativně nedávnou verzí MS Word. Také samostatný typografický systém, ale my budeme využívat jenom pro psaní matematických výrazů, kde je LaTeX nenahraditelný.

2.3. K syntaxi v jazyce Python#

  • záleží na mezerách na začátku řádku

    • příkazy tvořící hlavní tělo začínají na začátku řádku

    • bloky uvnitř cyklů a podmínek jsou odsazeny o pevný počet mezer (doporučené jsou čtyři pro jednotlivé úrovně)

  • zlom řádku může být uvnitř závorek s argumentem funkce a uvnitř závorek pro seznamy, potom nezáleží na odsazení

  • komentáře jsou jednořádkové a uvozeny znakem #

  • argumenty funkce jsou v kulatých závorkách, pořadové číslo položky v seznamu nebo ve slovníku je v hranatých závorkách,

  • doporučený styl podle Style guide

pocet_opakovani = 10 # promenne pojmenovavame tak, aby nazev vypovidal o obsahu dat
pocet_velkych_cisel = 0
"""
Při práci nemusíme vypisovat celé jméno proměnné, ale můžeme používat 
doplňování kódu, kdy napíšeme jenom prvních několik písmen a po stisku 
domluvené klávesy (zpravidla tabelátor) se název buď doplní, nebo, 
je-li více variant, se nabídnou možná doplnění pomocí menu.
V tomto textu též vidíte možnost víceřádkových komentářů. Stačí je 
napsat jako víceřádkové řetězce, tj. řetězce uvozené a ukončené třemi 
uvozovkami.
"""
for i in range(pocet_opakovani):
    if i<5:
        # tisk informace o cisle i
        print(f"Číslo {i} je malé")
    else:
        print(
            f"Číslo {i} je velké"
            )
        pocet_velkych_cisel = pocet_velkych_cisel + 1
print(
    f"Vyskytlo se celkem {pocet_velkych_cisel} velkych cisel"
)        

Číslo 0 je malé
Číslo 1 je malé
Číslo 2 je malé
Číslo 3 je malé
Číslo 4 je malé
Číslo 5 je velké
Číslo 6 je velké
Číslo 7 je velké
Číslo 8 je velké
Číslo 9 je velké
Vyskytlo se celkem 5 velkych cisel

Všimněte si mimo jiné, že Python počítá a indexuje od nuly, podobně jako JavaScript a některé další jazyky. První položka v seznamu má index nula, druhá jedna atd.

V argumentu příkazu print jsou použity takzvané f-řetězce, které usnadňují sestavení textu obsahujícího proměnné.

2.4. Aritmetika s čísly#

a = 4 # promenna a obsahuje nastavenou hodnotu
b = a + 2  # promenna b bude o dve vetsi nez promenna a
a = b**2   # promenna a se nahradi druhou mocninnou promenne b, promenna b zustava na sve hodnote
a  # tisk hodnoty promenne, vystup posledniho vypoctu se tiskne, neni nutne pouzivat print

36

Proměnné si udrží hodnoty i v dalších políčkách. V dalším políčku zmenšíme hodnotu \(a\) o 30.

a-30

6

Operace se zapisují běžným způsobem jako například v Excelu, pouze umocňování se označuje dvojicí hvězdiček. Takto vypadá druhá mocnina trojky.

3**2

9

2.4.1. Úkol 1#

Následující políčko s kódem 1**2 + 2**2 + 3**2 + 4**2 sčítá druhé mocniny přirozených čísel až do čísla 4. Opravte políčko tak, aby sečetlo druhou mocninu přirozených čísel až do čísla 6.

1**2 + 2**2 + 3**2 + 4**2

30

A pokud se vám úkol povedl, podívejme se, jak by úlohu řešil zkušenější zpracovatel dat. Následující kód je sice o něco delší, ale dá se snadno modifikovat pro sečtení mnohem obsáhlejšího seznamu čísel.

import numpy as np # nacteni knihovny
data = np.arange(1,7) # vytvoreni seznamu s cisly od 1 do 6
print(data) # tisk pro kontrolu
sum(data**2) # součet druhých mocnin

[1 2 3 4 5 6]

91

2.5. Hrátky s textem#

2.5.1. Podřetězce#

Textový řetezec se bere jako seznam znaků a je možné ho ukládat do proměnná, přistupovat k prvnímu nebo poslednímu znaku, k několika prvním nebo několika posledním znakům, ke skupině znaků uprostřed atd. Pozor na to, že Python indexuje od nuly a první znak má tedy index nulový. Pokud je index záporný, znamená to pořadí od konce.

retezec="MENDELU"
retezec

'MENDELU'

retezec[0]

'M'

retezec[-2]

'L'

retezec[:4]

'MEND'

retezec[-3:]

'ELU'

retezec[2:4]

'ND'

len(retezec)

7

Tyto techniky s přístupem k obsahu podle indexu využijeme, když budeme mít data v seznamu a budeme chtít přistupovat například k první nebo poslední hodnotě, nebo k několika prvním či několika posledním hodnotám. Analogicky jako pro řetězce indexování funguje pro data v polích čísel nebo data v tabulkách.

2.5.2. Sestavování textových řetezců#

  • Dva textové řetězce je možno spojit sečtením.

  • Pokud potřebujeme spojit textový řetězec s číslem, je možné použít f-řetězce. Tyto řetězce mají ve složených závorkách proměnné nebo výrazy, jejichž hodnoty se mají dosadit. Před řetězcem je znak f. V možnostech f-řetězců je i formátovaná na daný počet desetinných míst, jak ukazuje následující příklad.

print("Jedna dvě, "+"Honza jde.") # spojení textových řetězců
pocet = 333
print(f"{pocet} střibrných stříkaček stříkalo přes {pocet:.2f} střech.")  # ukázka f-řetězce

Jedna dvě, Honza jde.
333 střibrných stříkaček stříkalo přes 333.00 střech.

2.6. Knihovny#

Jenom základní funkce jsou v Pythonu přístupny přímo. Další funkce načítáme ve formě knihoven. Pro práci s daty zpravidla nejprve importujeme knihovny pro numeriku, práci s datovými tabulkami a pro kreslení grafů. Přitom používáme pro knihovny obvyklé zkratky, například np namísto numpy.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

2.7. Práce se seznamem hodnot#

Následující kód ukazuje

  • jak se vytvoří seznam zadáním hodnot

  • jak se vytvoří nový seznam na základě předchozího seznamu

  • jak se vykreslí funkce, pokud máme seznam hodnot pro vodorovnou a svislou osu.

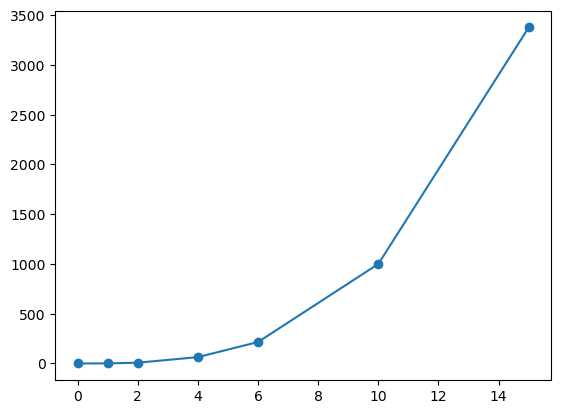
parametry = [0,1,2,4,6,10,15]
seznam = [i**3 for i in parametry]
plt.plot(parametry, seznam, "o-")
print(seznam)

[0, 1, 8, 64, 216, 1000, 3375]
../_images/4d737412c9f4d90952cf7d69195e9bcd5bfb20662d10728a4e1293d6b83dc5f6.png

Analogicky funguje následující trik, který ze seznamu hodnot nějakého parametru udělá seznam řetězců použitelných například pro popisky v grafu nebo pro jména sloupců.

Můžete si promyslet, jak bychom zařídili, aby výsledek obsahoval všechna čísla zapsaná s jedním místem za desetinnou tečkou. Využijte příklad s 333 stříbrnými stříkačkami výše.

# Můžete si promyslet, jak bychom zařídili, aby výsledek obsahoval všechna čísla zapsaná 
# s jedním místem za desetinnou tečkou. Využijte příklad s 333 stříbrnými stříkačkami výše.
r = [1,1.5,2,2.5,3]
[f"r={hodnota}" for hodnota in r]
# Vysledek je ['r=1', 'r=1.5', 'r=2', 'r=2.5', 'r=3']
# Raději bychom ['r=1.0', 'r=1.5', 'r=2.0', 'r=2.5', 'r=3.0']

['r=1', 'r=1.5', 'r=2', 'r=2.5', 'r=3']

Podrobněji o tomto tvaru zápisu zde. Praktické využití je například zde

2.8. Práce s poli np.array#

S poli typu np.array se pracuje podobně jako se seznamy ale dokážeme s nimi dělat rovnou matematické operace a zápis je pohodlnější.

# S polem typu array je možné provést většinu matematických operací najednou pro všechny prvky.
# Pole můžeme vygenerovat pomocí prvního a posledního prvku a příkazu np.linspace.
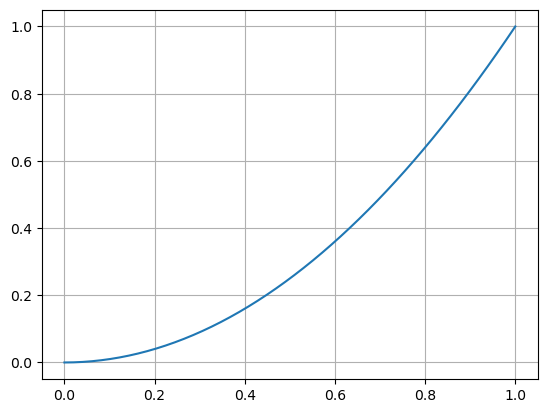
N = 1
x = np.linspace(0,N)
y = x**2 
plt.plot(x,y)
plt.grid()
# Pokud kód hlásí chybu, že není definován výraz np, nenačetli jste knihovny pro práci s daty, viz políčko výše se 
# třemi řádky začínajícími slovem import.
../_images/4e39fd791f37fc4ae13ae8fad598e97b19c560753e1b942beec66a9f26f662ac.png

2.8.1. Úkol 3#

Nakreslete graf třetí mocniny na intervalu \((-1,1)\).

# Sem vložte příkazy pro nakreslení grafu funkce x**3 na intervalu od -1 do 1.

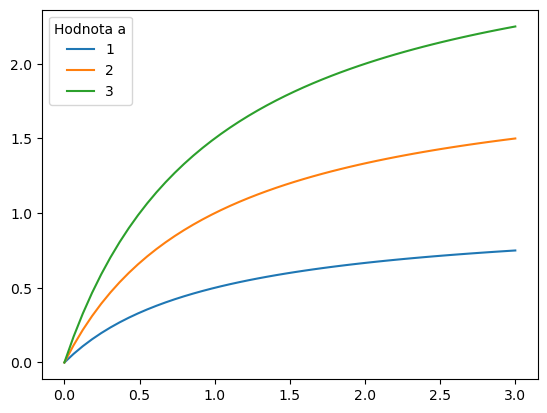
2.8.2. Hollingova funkce#

Můžeme nakreslit funkce

\[y=\frac{ax}{x+b}\]
pro různé hodnoty \(a\). Vyzkoušejte si následující příkazy. Pokuste se modifikovat kód tak, aby kreslil funkci
\[y=\frac{ax^2}{x^2+b}.\]
Abyste zachovali i přednastavené příkazy, pole si nejdřív překopírujte.

a_seznam = [1,2,3]
b = 1
x = np.linspace(0,3)
for a in a_seznam:
    plt.plot(x,a*x/(x+b))
plt.legend(a_seznam, title="Hodnota a")

<matplotlib.legend.Legend at 0x7fdd641817c0>
../_images/4133faf60ae06825e66530ce35120fe1431a0099829d00e7970efdcbbaba3a08.png

2.9. Úkol pro samostatně pracující#

Pokuste se modifikovat kód tak, aby nadpis grafu byl „Hodnota parametru“ a popisky křivek „a=1“, „a=2“, „a=3“. Popisky vygenerujte ze seznamu a_seznam tak, aby se automaticky přizpůsobily při změně parametrů, pro které křivky kreslíme.

2.10. Tabulky, pandas#

Výhodné je pracovat s daty v tabulkách. Tím totiž máme k dispozici širokou škálu nástrojů pro práci s daty, od kreslení, přes filtrování atd. Zpracování tabulek je běžná činnost, ke které js spousta návodů a tutoriálů. Nám bude stačit tvorba tabulek a vykreslení dat. Následující ukázka demonstruje tvorbu tabulky sloupec po sloupci. Nejprve se nadefinuje prázdná tabulka s přednastavenými řádky podle proměnné x a poté se do sloupců vloží data.

Pro práci používáme knihovnu pandas, kterou obvykle načítámne pod zkratkou pd. Tabulka se v této knihovně nazývá dataframe. Pokud pracujeme s jednou tabulkou, nepotřebujeme v názvu proměnné obsahující tuto tabulky mít popis dat a obvykle se jako proměnná používá df.

x = np.linspace(0,5,1001)
df = pd.DataFrame(index=x)
df["Holling-I"] = np.minimum(x,1)
df["Holling-II"] = x/(x+1)
df["Holling-III"] = x**2/(x**2+1)
df["prumer"] = (df["Holling-I"] + df["Holling-II"] + df["Holling-III"])/3
df.head() # vytiskne začátek tabulky
Holling-I Holling-II Holling-III prumer
0.000 0.000 0.000000 0.000000 0.000000
0.005 0.005 0.004975 0.000025 0.003333
0.010 0.010 0.009901 0.000100 0.006667
0.015 0.015 0.014778 0.000225 0.010001
0.020 0.020 0.019608 0.000400 0.013336

Poznámka: předchozí výpočet průměru tří hodnot byl jenom ilustrativní. V praxi by se na toto použila přednastavená funkce, která dokáže průměr vypočítat z celé tabulky. Volba axis určuje, zda se průměrují hodnoty v řádkách nebo ve sloupcích. Vyzkoušejte si axis=0 nebo si vyzkoušejte tuto hodnotu vynechat.

df.mean(axis=1)

0.000    0.000000
0.005    0.003333
0.010    0.006667
0.015    0.010001
0.020    0.013336
           ...   
4.980    0.931339
4.985    0.931410
4.990    0.931482
4.995    0.931553
5.000    0.931624
Length: 1001, dtype: float64

df.plot()

<Axes: >
../_images/a49d8e3f20c822d1dfde044111757311b91127ffa78a273530e745d6194e4305.png

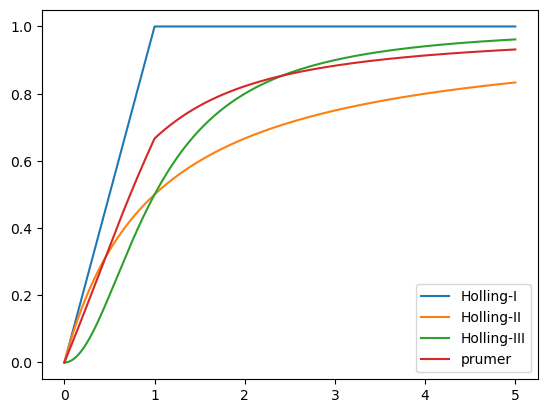
Tabulky je možno použít k operacím se sloupci podobně jako to znáte z Excelu, ale přehledněji.

Tabulky využijeme k ukládání stejně dlouhých datových řad. Výhodou je, že tabulky mají mnoho nástrojů na kreslení, manipulaci se sloupci a podobně. Využijeme u modelů, kde řešením dostaneme časový průběh pro více nastavení. Nemusíme kreslit každou křivku samostatně, ale nakreslíme je jedním příkazem.

2.11. Dva obrázky pod sebou, data z tabulky#

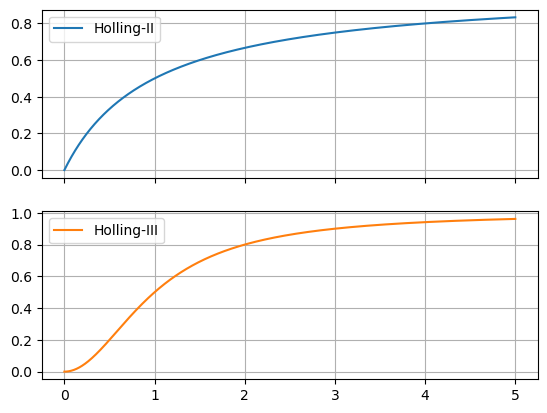
Někdy chceme nakreslit do jednoho obrázku dvě funkce se společným definičním oborem, ale značně rozdílnými funkčními hodnotami. Řešením je buď nakreslit obrázky pod sebe a se sdílenou vodorovnou osou (viz níže), nebo nakreslit do jednoho obrázku obě funkce, ale každou s jiným měřítkem na svislé ose, tedy použít v jednom obrázku dvě svislé osy (viz Google a hesla matplotlib a twinx).

# vykresleni dat do obrazku
ax = df[["Holling-II","Holling-III"]].plot(subplots=True)

# # dekorace grafu
ax[0].grid() # vykresleni mrizky
ax[1].grid() # vykresleni mrizky

# Tisk začátku tabulky pro kontrolu
df.head(10)
Holling-I Holling-II Holling-III prumer
0.000 0.000 0.000000 0.000000 0.000000
0.005 0.005 0.004975 0.000025 0.003333
0.010 0.010 0.009901 0.000100 0.006667
0.015 0.015 0.014778 0.000225 0.010001
0.020 0.020 0.019608 0.000400 0.013336
0.025 0.025 0.024390 0.000625 0.016672
0.030 0.030 0.029126 0.000899 0.020008
0.035 0.035 0.033816 0.001224 0.023347
0.040 0.040 0.038462 0.001597 0.026686
0.045 0.045 0.043062 0.002021 0.030028
../_images/37f6b0006032b6709884d995215899f3c3265ab301be8aa0c26ef36e850e4656.png

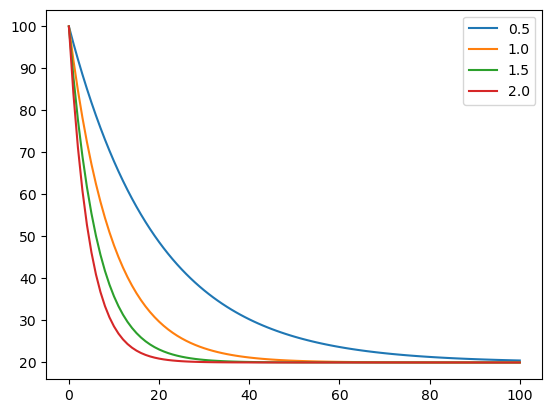
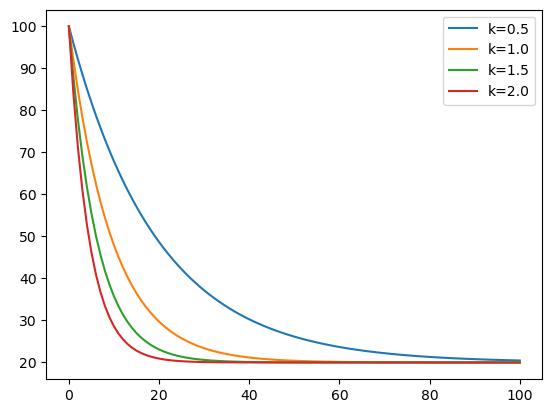
2.12. Model ochlazování kávy (volitelně)#

V následujícícm je minimalistická verze modelu ochlazování kávy podle rovnice

\[\frac{\mathrm dT}{\mathrm dt}=-k (T-20), \quad T(0)=100\]
řešená s krokem 0.1 Eulerovou metodou. Teplota v dalším okamžiku se určí podle vzorce
\[T_0=100, \quad T_{n+1}=T_n - k (T_n-20) \Delta t,\]
kde \(\Delta t\) je zvolený časový krok, během něhož považujeme rychlost změny za konstantní.

Pro různé hodnoty parametru. Při použití proměnné typu dictionary tabulka má data ve sloupcích. (Při použití seznamu by vznikla tabulka s daty v řádcích a pro většinu operací by se musela transponovat.) Můžete si vyzkoušet modifikace, jak je ochlazování z různých počátečních podmínek nebo ochlazování při různé teplotě okolí.

### Minimalistická verze modelování ochlazování kávy
T = 100
N = 100
seznam = [0.5,1,1.5,2]
teploty = {
    f'k={k:.1f}' : 
    [T:=100] + [T := T - k * (T-20) * 0.1 for i in range (N)]  
        for k in seznam
    }
df_teplota = pd.DataFrame(teploty)
df_teplota
k=0.5 k=1.0 k=1.5 k=2.0
0 100.000000 100.000000 100.000000 100.000
1 96.000000 92.000000 88.000000 84.000
2 92.200000 84.800000 77.800000 71.200
3 88.590000 78.320000 69.130000 60.960
4 85.160500 72.488000 61.760500 52.768
... ... ... ... ...
96 20.581509 20.003239 20.000013 20.000
97 20.552433 20.002915 20.000011 20.000
98 20.524811 20.002623 20.000010 20.000
99 20.498571 20.002361 20.000008 20.000
100 20.473642 20.002125 20.000007 20.000

101 rows × 4 columns

df_teplota.plot()

<Axes: >
../_images/24fa081b29eff1ee2e5a9a1247cec8bd444c9515c045168a0738d7075fc86b7e.png 
### Minimalistická verze modelování ochlazování kávy, tabulka s daty vodorovne
T = 100
N = 100
seznam = [0.5,1,1.5,2]
teploty = [ 
    [T:=100] + [T := T - k * (T-20) * 0.1 for i in range (N)]  
        for k in seznam 
]
df_teplota_vorodovne = pd.DataFrame(teploty, index=seznam)
df_teplota_vorodovne
0 1 2 3 4 5 6 7 8 9 ... 91 92 93 94 95 96 97 98 99 100
0.5 100 96.0 92.2 88.59 85.1605 81.902475 78.807351 75.866984 73.073635 70.419953 ... 20.751516 20.713940 20.678243 20.644331 20.612114 20.581509 20.552433 20.524811 20.498571 20.473642
1.0 100 92.0 84.8 78.32 72.4880 67.239200 62.515280 58.263752 54.437377 50.993639 ... 20.005485 20.004936 20.004443 20.003998 20.003599 20.003239 20.002915 20.002623 20.002361 20.002125
1.5 100 88.0 77.8 69.13 61.7605 55.496425 50.171961 45.646167 41.799242 38.529356 ... 20.000030 20.000026 20.000022 20.000019 20.000016 20.000013 20.000011 20.000010 20.000008 20.000007
2.0 100 84.0 71.2 60.96 52.7680 46.214400 40.971520 36.777216 33.421773 30.737418 ... 20.000000 20.000000 20.000000 20.000000 20.000000 20.000000 20.000000 20.000000 20.000000 20.000000

4 rows × 101 columns

df_teplota_vorodovne.T
0.5 1.0 1.5 2.0
0 100.000000 100.000000 100.000000 100.000
1 96.000000 92.000000 88.000000 84.000
2 92.200000 84.800000 77.800000 71.200
3 88.590000 78.320000 69.130000 60.960
4 85.160500 72.488000 61.760500 52.768
... ... ... ... ...
96 20.581509 20.003239 20.000013 20.000
97 20.552433 20.002915 20.000011 20.000
98 20.524811 20.002623 20.000010 20.000
99 20.498571 20.002361 20.000008 20.000
100 20.473642 20.002125 20.000007 20.000

101 rows × 4 columns

df_teplota_vorodovne.T.plot()

<Axes: >
../_images/30772321dfe05050730df2cf53912911fa9518d97e70504d03479ae89e653647.png
Obsah