10. Modely dravce a kořisti

Jako modely dravce a kořisti se nazývají modely zpravidla dvou populací, kdy jedna z populací (kořist) se přirozeně rozmnožuje a rychlost jejího růstu je zpomalována působením predátora, zatímco druhá z populací (predátor) má bez přítomnosti kořisti negativní rychlost růstu a může růst pouze v přítomnosti dostatečného množsví kořisti.

Více o ekologickém pozadí těchto modelů viz [3] kapitola 10.

10.1. Lotkův a Volterrův model

Lotkův Volterrův model jsme poznali v úvodní kapitole k autonomním systémům. Tento model předpokládá rychlost růstu úměrnou velikosti populace kořisti (není tedy zahrnuta nosná kapacita prostředí a s ní související vnitrodruhová konkurence) a tato rychlost je snižována přítomností dravce rychlostí úměrnou velikosti populace dravce i kořisti. O populaci dravce se v tomto modelu předpokládá, že bez potravy vymírá rychlostí úměrnou velikosti této populace a kladný člen vyjadřující růst populace v přítomnosti kořisti je úměrný velikostem obou populací, tj. velikosti populace dravce i kořisti. Přestože model přirozeně ignoruje nosnou kapacitu prostředí, nemusí tato skutečnost model diskvalifikovat z aplikací, protože samotná přítomnost predátora může způsobit, že populace kořisti je trvale dostatečně pod nosnou kapacitou a mezidruhová konkurence v populaci kořisti nemá příliš velký vliv.

Jsou-li \(x\) a \(y\) velikosti populací kořisti a dravce, má matematický model tvar

\[ \begin{aligned}\frac{\mathrm dx}{\mathrm dt}&=ax-bxy,\\\frac{\mathrm dy}{\mathrm dt}&=-cy+dxy.\end{aligned} \]

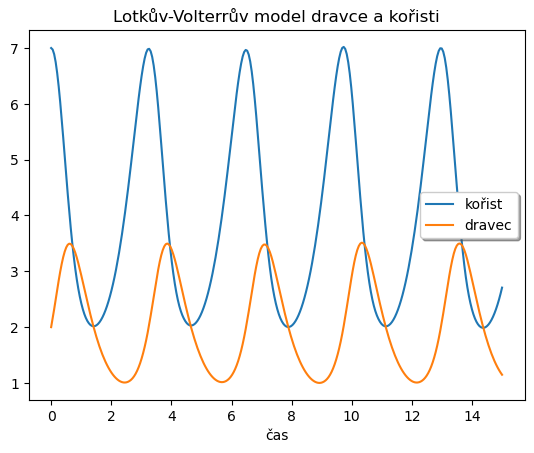
Řešením tohoto modelu jsou periodické trajektorie. Ve cvičení prozkoumáme, zda mají všechny trajektorie stejnou periodu, či nikoliv.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

Show code cell source Hide code cell source

def prey(x,y,a=2,b=1):
    return a*x - b*x*y

def predator(x,y,c=2,d=0.5):
    return -c*y+d*x*y

def model(t,X):
    x,y = X
    return [prey(x,y),predator(x,y)]

meze = [0,15]
pocatecni_podminka = [7, 2]


t = np.linspace(*meze, 300)
sol = solve_ivp(
    model, 
    meze, # interval pro reseni
    pocatecni_podminka, # pocatecni podminka
    t_eval=t
)

plt.plot(t, sol.y.T)
plt.xlabel('čas')
plt.legend(['kořist', 'dravec'], shadow=True)
plt.title('Lotkův-Volterrův model dravce a kořisti')
plt.show()

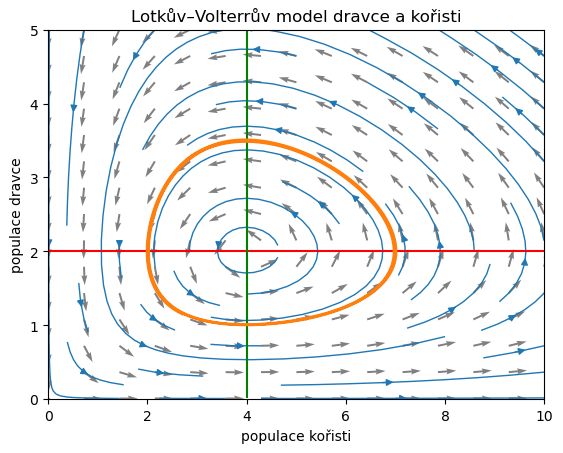
Show code cell source Hide code cell source

x, y = np.meshgrid(np.linspace(0.01, 10, 15), 
                   np.linspace(0.01, 5, 15))

# Komponenty vektoroveho pole
u,v = model(0,[x,y])
M = np.sqrt(u**2+v**2) # velikost vektoru

fig,ax = plt.subplots()
ax.quiver(x,y,u/M,v/M,color='gray',units='xy', angles='xy') # vykresleni s jednotkovou delkou
integralni_krivky = ax.streamplot(x, y, u, v, density=0.5, linewidth=1)

t = np.linspace(*meze,800)
reseni = solve_ivp(model,
                   meze,
                   pocatecni_podminka,
                   t_eval = t
                  )

x_nulcline = plt.contour(x, y, prey(x,y), [0], colors='red')
y_nulcline = plt.contour(x, y, predator(x,y), [0], colors='green')

ax.plot(*reseni.y)
ax.set(
    ylim=(0,None), 
    xlim=(0,None),
xlabel="populace kořisti",
ylabel="populace dravce",
title="Lotkův–Volterrův model dravce a kořisti");

10.2. Rosenzweigův a MacArthurův model

Obecněji je možné předpokládat růst populace kořisti závislý na hustotě populace a nelineární trofickou funkci predátora. Toto vede na model

\[ \begin{aligned}\frac{\mathrm dx}{\mathrm dt}&=x\phi(x)-yf(x,y),\\\frac{\mathrm dy}{\mathrm dt}&=-cy+dyf(x,y),\end{aligned} \]

jehož řešení mohou vypadat například následovně.

Show code cell source Hide code cell source

def predator(x,y,c=0.04, d=0.1, m=4):
    return -c*y + d*x*y/(m+x)

def prey(x,y,r=1, b=0.3, K=10, m=4):
    return r*(1-x/K)*x-b*x*y/(m+x)

def model(t,X):
    x,y = X
    return [prey(x,y),predator(x,y)]

meze = [0,400]
t = np.linspace(*meze,2000)
pocatecni_podminky = [[2,12],[4,16],[2.5,16]]

populace = ["kořist","dravec"]
df = pd.DataFrame(
    columns = pd.MultiIndex.from_product(
        [
            [i for i in range(len(pocatecni_podminky))],
            populace
        ], names = ['počáteční podmínka', 'populace'])
)

for i,pocatecni_podminka in enumerate(pocatecni_podminky):
    reseni = solve_ivp(model,
                   meze,
                   pocatecni_podminka,
                   t_eval = t
                  ).y.T
    df[[(i,j) for j in populace]] = reseni
df

počáteční podmínka	0		1		2
populace	kořist	dravec	kořist	dravec	kořist	dravec
0	2.000000	12.000000	4.000000	16.000000	2.500000	16.000000
1	2.081806	11.985075	3.999522	16.032045	2.505855	15.995163
2	2.167149	11.972333	3.998101	16.064135	2.511873	15.990508
3	2.256029	11.961797	3.995754	16.096251	2.518052	15.986038
4	2.348415	11.953486	3.992499	16.128375	2.524389	15.981757
...	...	...	...	...	...	...
1995	3.346472	17.636679	1.248762	14.006835	1.082455	15.550477
1996	3.310200	17.655847	1.267999	13.961871	1.077136	15.492260
1997	3.273730	17.674061	1.288441	13.917847	1.072496	15.434021
1998	3.237050	17.691302	1.310128	13.874797	1.068537	15.375796
1999	3.200145	17.707555	1.333098	13.832754	1.065264	15.317619

2000 rows × 6 columns

Show code cell source Hide code cell source

fig,axs = plt.subplots(2,sharex=True)
axs[0].plot(t,df.xs(key="kořist",level=1,axis=1))
axs[1].plot(t,df.xs(key="dravec",level=1,axis=1))

for ax in axs:
    ax.grid()
    ax.set(ylabel="velikost populace")
    
axs[0].set(title="Kořist")    
axs[1].set(xlabel="čas",title="Dravec")
plt.suptitle("Rosenzweigův a MacArthurův model dravce a kořisti")
plt.tight_layout();

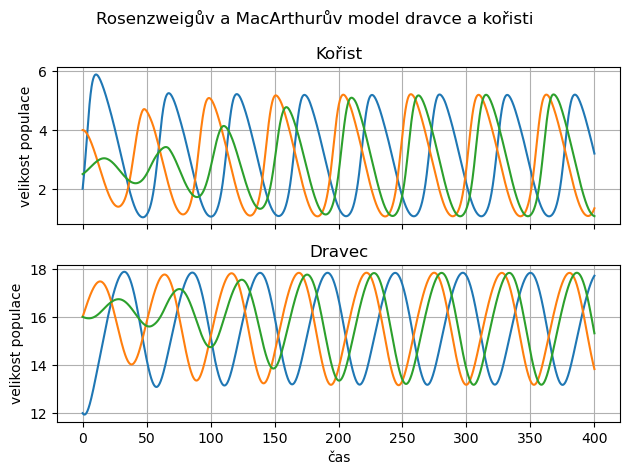
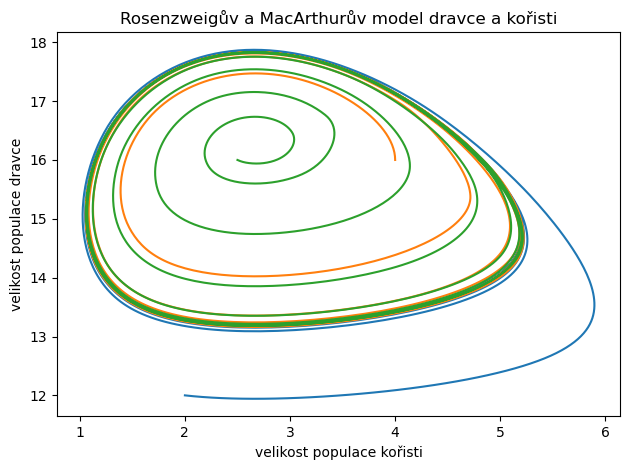
Nedostatkem Lotkova–Volterrova modelu to, že perioda cyklů závisí na počátečních podmínkách. Model Rosenzweigův a MacArthurův tímto nedostatkem netrpí, protože obsahuje jenom jeden cyklus a všechny trajektorie k němu konvergují. Perioda oscilujících řešení tedy bude stejná a řešení mohou být nanejvýš fázově posunuta, což je vidět z časového průběhu. Jednoznačnost cyklu je identifikovatelná z fázového portrétu.

Show code cell source Hide code cell source

fig,ax = plt.subplots()
for i in range(len(pocatecni_podminky)):
    ax.plot(*df[i].values.T)

ax.set(
    xlabel="velikost populace kořisti",
    ylabel="velikost populace dravce",
    title="Rosenzweigův a MacArthurův model dravce a kořisti")    
plt.tight_layout();

Kvůli překryvu křivek je možná vhodnější použít animaci.

Show code cell source Hide code cell source

# podle https://stackoverflow.com/questions/43445103/inline-animations-in-jupyter
import matplotlib.animation
plt.rcParams["animation.html"] = "jshtml"
plt.rcParams['figure.dpi'] = 100  
plt.ioff()

fig,ax = plt.subplots()
korist = df.xs(key="kořist",level=1,axis=1).values
dravec = df.xs(key="dravec",level=1,axis=1).values
ax.set(
    xlabel="velikost populace kořisti",
    ylabel="velikost populace dravce",
    title="Rosenzweigův a MacArthurův model dravce a kořisti",
    xlim=(korist.min()*0.95,korist.max()*1.05),
    ylim=(dravec.min()*0.95,dravec.max()*1.05)
)  

def animate(t):
    if t==0:
        ax.set_prop_cycle(None)           # reset cyklovače barev
    ax.plot(*df[t].values.T)

matplotlib.animation.FuncAnimation(fig, animate, frames=3)

Once Loop Reflect

(Předchozí animace vypnula interaktivní kreslení, musíme ho zase zapnout.)

Show code cell source Hide code cell source

plt.clf()
plt.ion();

Pro detailnější informaci můžeme do obrázku zahrnout i směrové pole a nulkliny.

Show code cell source Hide code cell source

korist = df.xs(key="kořist",level=1,axis=1).values
dravec = df.xs(key="dravec",level=1,axis=1).values

xmin, xmax = korist.min()*0.8, korist.max()*1.1
ymin, ymax = dravec.min()*0.9, dravec.max()*1.1

x, y = np.meshgrid(np.linspace(xmin, xmax, 15), 
                   np.linspace(ymin, ymax, 15))

# Komponenty vektoroveho pole
u,v = model(0,[x,y])
M = np.sqrt(u**2+v**2) # velikost vektoru

fig,ax = plt.subplots()
for i in range(len(pocatecni_podminky)):
    ax.plot(*df[i].values.T)
    
ax.quiver(x,y,u/M,v/M,color='gray',units='xy', angles='xy') # vykresleni s jednotkovou delkou
integralni_krivky = ax.streamplot(x, y, u, v, density=0.3)

x, y = np.meshgrid(np.linspace(xmin, xmax, 40), 
                   np.linspace(ymin, ymax, 40))

x_nulcline = plt.contour(x, y, predator(x,y), [0])
y_nulcline = plt.contour(x, y, prey(x,y), [0], colors='gray')


ax.set(
    xlabel="velikost populace kořisti",
    ylabel="velikost populace dravce",
    title="Rosenzweigův a MacArthurův model dravce a kořisti",
);

<Figure size 640x480 with 0 Axes>

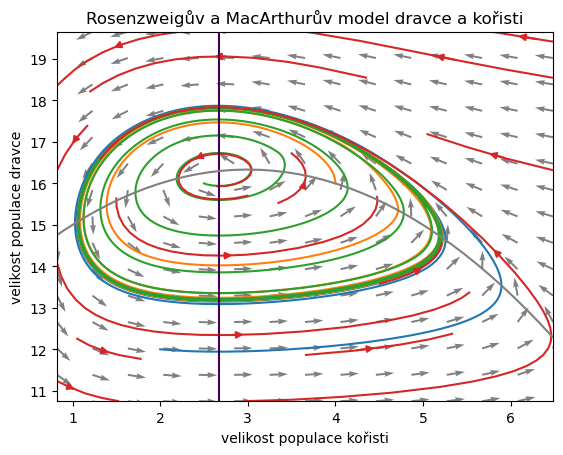
Poznámka: Zkuste změnou parametru \(c\) regulovat úmrtnost dravce. Všimněte si, že se model může stabilizovat, tj. nemusí docházet k oscilacím, ale populace mohou setrvávat na rovnovážné poloze. I toto v přírodě pozorujeme, že stavy dravce a kořisti (nebo býložravce a rostliny) jsou dlouhodobě stabilní.