Tabulky s hierarchickým indexem#

Tabulky s hierarchickým indexem umožňují v tabulce pracovat s daty, která mají složitější strukturu, než prosté dvourozměrné souhrny čísel. Například je možné pro různé scénáře (nastavení parametrů) řešit model s různými výchozími stavy (počátečními podmínkami) a vše zahrnout do jedné tabulky. Poté je možné například zpracovat všechny simulace s daným počátečním stavem (a libovolným nastavením dalších parametrů) nebo všechny simulace se s daným nastavením parametrů (a libovolnou počáteční podmínkou).

Ukážeme si na rovnici logistického růstu s konstantním lovem.

Rovnice

\[\frac{\mathrm dn}{\mathrm dt}=rn\left(1-\frac nK\right)-h\]

popisuje vývoj populace o velikosti \(n\) v prostředí s nosnou kapacitou \(K\). Budeme pro různou intenzitu lovu vždy sledovat řešení pro několik počátečních podmínek. Všechno zaznamenáme do tabulky a data z tabulky poté vykreslíme. Sloupec bude identifikován pomocí trojice hodnot, udávajících že jde o velikosti populací (a ne čas), dále intenzitu lovu a počáteční podmínku.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

pocatecni_podminka = [0.4]
meze = [0,10]

def rovnice(t, x, r=1, K=1, h=0):
    return r*x*(1-x/K) - h

def destrukce_populace(t,x,r=1,K=1,h=0):  # Pokud x klesne na nulu, zastavíme výpočet
    return x
destrukce_populace.terminal = True

t=np.linspace(*meze,101)  
seznam_h = [0,0.1,0.15,0.2,0.25,0.28]
seznam_pp = np.round(np.arange(0.1,1.2,0.05),2)

### Definice tabulky s víceúrovňovými nadpisy sloupců, MultiIndex
### https://pandas.pydata.org/docs/user_guide/advanced.html
iterables = [seznam_h,seznam_pp]
my_index = pd.MultiIndex.from_product(iterables, names=['lov', 'poč.podm.'])
df = pd.DataFrame(columns=my_index, dtype='float64', index=t)
df.index.name = "Čas"
df

lov	0.00										...	0.28
poč.podm.	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	...	0.70	0.75	0.80	0.85	0.90	0.95	1.00	1.05	1.10	1.15
Čas
0.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
0.1	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
0.2	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
0.3	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
0.4	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
9.6	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
9.7	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
9.8	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
9.9	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
10.0	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN

101 rows × 132 columns

Dále ve dvojitém cyklu pro každou počáteční podmínku a úroveň lovu najdeme řešení. Hledání řešení ukončíme při dosažení konce časového intervalu, nebo při dosažení nulové hodnoty pro velikost populace. Proto jsme tabulku založili rovnou se sloupci, které mají nedefinované hodnoty np.nan. Nyní vyměníme tolik položek ze začátku sloupce, kolik máme k dispozici vypočtených hodnot.

Tabulku vytiskneme, pro lepší přehlednost naležato.

for h in seznam_h:
    for pp in seznam_pp:
        reseni = solve_ivp(
                   lambda t,x:rovnice(t,x,h=h),
                   meze,
                   [pp],
                   t_eval=t, 
                   events=destrukce_populace,            
                   )
        df.loc[reseni.t,(h,pp)] = reseni.y.reshape(-1) # poté hodnoty zaměníme za vypočtené od začátku až po konec řešení
df.T   # vytiskneme tabulku naležato     

	Čas	0.0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	...	9.1	9.2	9.3	9.4	9.5	9.6	9.7	9.8	9.9	10.0
lov	poč.podm.
0.00	0.10	0.10	0.109367	0.119490	0.130409	0.142170	0.154811	0.168360	0.182841	0.198269	0.214654	...	0.998996	0.999076	0.999143	0.999201	0.999252	0.999299	0.999347	0.999399	0.999455	0.999507
	0.15	0.15	0.163201	0.177317	0.192371	0.208383	0.225362	0.243304	0.262194	0.282004	0.302695	...	0.999423	0.999458	0.999483	0.999501	0.999515	0.999528	0.999543	0.999564	0.999595	0.999633
	0.20	0.20	0.216481	0.233921	0.252314	0.271641	0.291872	0.312962	0.334858	0.357490	0.380778	...	0.999461	0.999512	0.999559	0.999601	0.999639	0.999673	0.999704	0.999732	0.999757	0.999780
	0.25	0.25	0.269214	0.289339	0.310332	0.332133	0.354672	0.377873	0.401645	0.425892	0.450506	...	0.999576	0.999593	0.999616	0.999648	0.999681	0.999712	0.999739	0.999764	0.999786	0.999807
	0.30	0.30	0.321410	0.343605	0.366510	0.390029	0.414061	0.438501	0.463241	0.488165	0.513157	...	0.999715	0.999717	0.999718	0.999720	0.999724	0.999733	0.999751	0.999774	0.999796	0.999815
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
0.28	0.95	0.95	0.927749	0.907292	0.888347	0.870799	0.854539	0.839464	0.825467	0.812447	0.800302	...	0.436736	0.433314	0.429846	0.426329	0.422760	0.419135	0.415451	0.411704	0.407890	0.404005
	1.00	1.00	0.973331	0.949011	0.926629	0.906047	0.887138	0.869770	0.853805	0.839105	0.825525	...	0.441710	0.438351	0.434949	0.431502	0.428006	0.424460	0.420859	0.417201	0.413482	0.409700
	1.05	1.05	1.018480	0.989968	0.963915	0.940152	0.918513	0.898820	0.880888	0.864520	0.849509	...	0.446593	0.443288	0.439944	0.436559	0.433129	0.429653	0.426128	0.422551	0.418919	0.415230
	1.10	1.10	1.063204	1.030200	1.000301	0.973271	0.948868	0.926839	0.906917	0.888824	0.872266	...	0.450776	0.447519	0.444226	0.440895	0.437522	0.434106	0.430645	0.427135	0.423575	0.419962
	1.15	1.15	1.107508	1.069714	1.035770	1.005349	0.978114	0.953714	0.931781	0.911931	0.893763	...	0.455037	0.451865	0.448657	0.445411	0.442123	0.438792	0.435414	0.431987	0.428507	0.424973

132 rows × 101 columns

Na závěr tabulku vykreslíme. Například všechny křivky odpovídající stejné intenzitě lovu vykreslíme stejnou barvou.

for i,h in enumerate(seznam_h):        
    plt.plot(df.index,df[h],color=f"C{i}",label=h,alpha=0.4,lw=1) 

ax = plt.gca()
ax.set(
    title = "Dynamika populace\n v závislosti na intenzitě lovu a počáteční podmínce",
    xlabel="Čas",
    ylabel="Velikost populace",
)
# Návod jak seskupit položky legendy je na https://stackoverflow.com/questions/26337493/pyplot-combine-multiple-line-labels-in-legend
handles, labels = ax.get_legend_handles_labels()
labels, ids = np.unique(labels, return_index=True)
handles = [handles[i] for i in ids]
ax.legend(handles, labels, title="Intenzita lovu");

../_images/7ed389139867433d1c2203d94af44e1ad333ed3aab8e5e73d7f7331b13de14a6.png

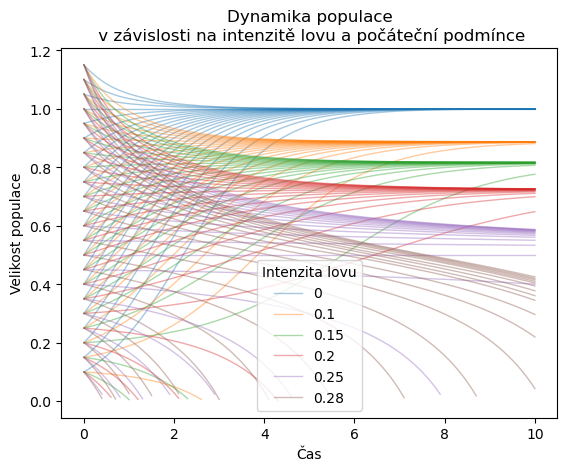
Na závěr ukázka, jak snadno z tabulky vybereme všechna řešení s počáteční podmínkou 0.2. Jde vidět, že tři hodnoty lovu vedou k destrukci populace v konečném čase. Jako obvykle, je několik možností jak cíle dosáhnout, ukážeme si dvě z nich.

df.loc[:,(slice(None),0.2)]

lov	0.00	0.10	0.15	0.20	0.25	0.28
poč.podm.	0.2	0.2	0.2	0.2	0.2	0.2
Čas
0.0	0.200000	0.200000	0.200000	0.200000	0.200000	0.200000
0.1	0.216481	0.206182	0.201031	0.195877	0.190722	0.187628
0.2	0.233921	0.212738	0.202125	0.191493	0.180838	0.174433
0.3	0.252314	0.219677	0.203285	0.186822	0.170284	0.160327
0.4	0.271641	0.227018	0.204517	0.181849	0.159020	0.145247
...	...	...	...	...	...	...
9.6	0.999673	0.883717	0.765607	NaN	NaN	NaN
9.7	0.999704	0.883966	0.768472	NaN	NaN	NaN
9.8	0.999732	0.884200	0.771186	NaN	NaN	NaN
9.9	0.999757	0.884423	0.773758	NaN	NaN	NaN
10.0	0.999780	0.884635	0.776194	NaN	NaN	NaN

101 rows × 6 columns

df.xs(level="poč.podm.", key=0.2, axis=1)

lov	0.00	0.10	0.15	0.20	0.25	0.28
Čas
0.0	0.200000	0.200000	0.200000	0.200000	0.200000	0.200000
0.1	0.216481	0.206182	0.201031	0.195877	0.190722	0.187628
0.2	0.233921	0.212738	0.202125	0.191493	0.180838	0.174433
0.3	0.252314	0.219677	0.203285	0.186822	0.170284	0.160327
0.4	0.271641	0.227018	0.204517	0.181849	0.159020	0.145247
...	...	...	...	...	...	...
9.6	0.999673	0.883717	0.765607	NaN	NaN	NaN
9.7	0.999704	0.883966	0.768472	NaN	NaN	NaN
9.8	0.999732	0.884200	0.771186	NaN	NaN	NaN
9.9	0.999757	0.884423	0.773758	NaN	NaN	NaN
10.0	0.999780	0.884635	0.776194	NaN	NaN	NaN

101 rows × 6 columns