Řešení diferenciální rovnice

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

Pravou stranu rovnice je výhodné mít definovánu jako samostatnou funkci. Má první argument čas, druhý argument derivovanou veličinu, může mít parametry a tyto parametry mohou mít implicitní hodnoty. (Implicitní hodnoty se použijí, pokud není zadána jiná hodnota parametru.)

Následující funkce je pravou stranou logistické rovnice

\[\frac{\mathrm dy}{\mathrm dt}=ry\left(1-\frac yK\right).\]

def rovnice(t,y,r=1,K=1):
    return r*y*(1-y/K)

Nastavení počátečních podmínek je vhodné udělat mimo příkaz řešící rovnici, aby se případné modifikace dělaly vždy na jednom místě. Je vhodné sadu příkazů rozdělit do více buněk, aby se nepočítalo to, co není nutné počítat znovu.

pocatecni_podminka = [0.1]
meze = [0,10]
t = np.linspace(0,10,100)

Varianta 1: Chceme funkční předpis

Při volání funkce solve_ivp rovnou použijeme metodu sol. Výsledkem je funkce, do keré můžeme dosazovat libovolný čas mezi dolní a horní mezí a získáme hodnotu řešení v daném čase. Můžeme také dosazovat několik hodnot času současně a získáme funkční hodnotu pro každý časový okamžik.

reseni_spojite = solve_ivp(
                   rovnice,
                   meze,
                   pocatecni_podminka,
                   dense_output=True,
                   ).sol

reseni_spojite(1)

array([0.23199499])

reseni_spojite(t).shape

(1, 100)

reseni_spojite(t)[0].shape

(100,)

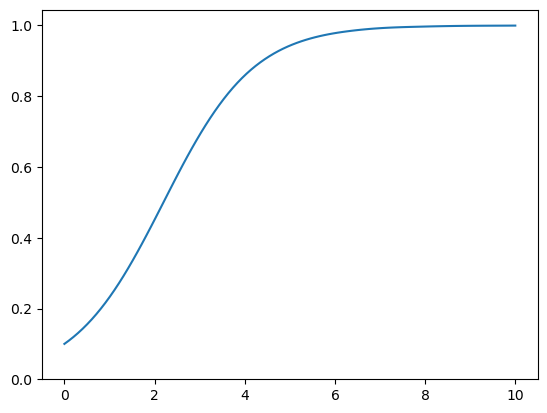
plt.plot(t,reseni_spojite(t)[0])
ax = plt.gca()
ax.set(ylim=(0,None));

Varianta 2: Chceme data pro předem známé časy

Hodnoty času, pro které se má určit funkční hodnota řešení, se zadají při volání příkazu solve_ivp pomocí parametru t_eval.

reseni_data = solve_ivp(
                   rovnice,
                   meze,
                   pocatecni_podminka,
                   t_eval=t,
                   ).y
reseni_data.shape

(1, 100)

plt.plot(t,reseni_data[0])
ax = plt.gca()
ax.set(ylim=(0,None));

Různé hodnoty parametrů

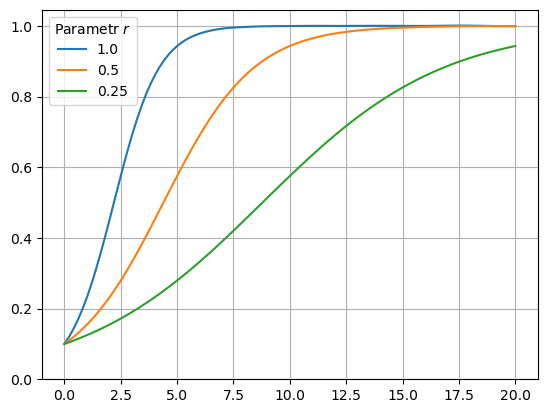
Pokud chceme určit chování řešení pro různé hodnoty parametrů, je nejvýhodnější řešit rovnici v každém případě pro stejné hodnoty času a výsledek uspořádat jako sloupce tabulky. Vytvoříme tedy seznam obsahující jednotlivé funkční hodnoty, sestavíme z nich tabulku a přidáme sloupec s časem. Poté můžeme dělat cokoliv, například řešení vykreslit.

parametry_r = [1,0.5,0.25]
meze_2 = [0,20]
t_2 = np.linspace(0,20,100)
reseni_data = [
                solve_ivp(
                   lambda t,x: rovnice(t,x,r=r),
                   meze_2,
                   pocatecni_podminka,
                   t_eval=t_2,
                   ).y[0]
                for r in parametry_r
            ]
reseni_data = pd.DataFrame(np.array(reseni_data).T,columns=parametry_r)
reseni_data.index = t_2
reseni_data

	1.00	0.50	0.25
0.000000	0.100000	0.100000	0.100000
0.202020	0.119702	0.109465	0.104638
0.404040	0.142664	0.119707	0.109465
0.606061	0.169211	0.130767	0.114487
0.808081	0.199558	0.142683	0.119707
...	...	...	...
19.191919	0.999366	0.999297	0.931092
19.393939	0.999170	0.999342	0.934262
19.595960	0.999041	0.999394	0.937297
19.797980	0.999009	0.999451	0.940201
20.000000	0.999110	0.999504	0.942978

100 rows × 3 columns

ax = reseni_data.plot()
plt.legend(title=r"Parametr $r$")
ax.set(ylim=(0,None))
ax.grid()