6. Lineární algebra, matice

Co se dozvíte v tomto textu

V následujících odstavcích se budeme věnovat problematice mnohorozměrných veličin. Ty se používají například ke sledování populace rozdělené do několika věkových nebo vývojových tříd a umožňují formulovat modely zohledňující tuto strukturu.

Díky tomu je možno například identifikovat účinnou strategii ochrany živočišných druhů. Analýza pomocí prostředků lineární algebry umožní rozhodnout, zda je pro přežití populace nějakého druhu důležitější přežití dospělých jedinců podílejících se na reprodukci, nebo produkce mláďat. Umožní rozhodnout, zda pro šetrnou těžbu lesa je výhodnější kácení mladých nebo starých stromů. Umožní nastavit lov, který buď neohrozí stabilitu lovené populaci, nebo naopak (při eliminaci škůdců) dokáže zasáhnout populaci na nejcitlivějším místě.

Foto: Tuleň kuželozubý. Na modelu tohoto tuleně si ukážeme možnosti modelování populace s věkovou strukturou. Autor George Hodan, https://www.publicdomainpictures.net/.

Lineární algebra je odvětví matematiky, zabývající se vektory a obecně mnohorozměrnými veličinami.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
np.set_printoptions(suppress=True);

6.1. Vektory

Vektorem rozumíme uspořádanou \(n\)-tici objektů, pro které má smysl operace sčítání a násobení číslem. Počet komponent v této \(n\)-tici se nazývá dimenze vektoru. Tyto komponenty jsou zpravidla čísla nebo skalární funkce. Aby se s vektory dalo rozumně pracovat, musí na nich být definovány matematické operace, které tvoří vhodnou matematickou strukturu. Například operace musí mít neutrální prvek a každý vektor musí mít opačný prvek.

Definice (Vektory, vektorový prostor)

Množinu \(V\) uspořádaných \(n\)-tic \((a_1, a_2,\dots, a_n)\) s operacemi sčítání a násobení reálným číslem definovanými

\[ \begin{gathered} (a_1, a_2,\dots, a_n)+(b_1, b_2,\dots, b_n)=(a_1+b_1, a_2+b_2,\dots, a_n+b_n)\\ c\cdot (a_1, a_2,\dots, a_n)=(c\cdot a_1, c\cdot a_2,\dots,c\cdot a_n) \end{gathered} \]

pro všechna \(c\in\mathbb R\) a \((a_1, a_2,\dots, a_n),(b_1, b_2,\dots, b_n)\in V\) nazýváme vektorovým prostorem. Prvky tohoto prostoru nazýváme vektory. Prvky \(a_1, \dots, a_n\) nazýváme složky vektoru \((a_1,a_2,\dots, a_n)\). Číslo \(n\) nazýváme dimenze prostoru \(V\).

Vektorový prostor, jehož komponenty jsou uspořádané \(n\)-tice reálých čísel označujeme \(\mathbb R^n\).

Často pracujeme se sloupcovými vektory. Zápis je potom přehlednější.

6.2. Lineární kombinace

Definice (Lineární kombinace)

Nechť \(\vec u_1\), \(\vec u_2\), \(\dots\) \(\vec u_k\) je konečná posloupnost vektorů z vektorového prostoru \(V\). Vektor \(\vec u\), pro který platí

\[ \vec u=t_1\vec u_1+t_2\vec u_2+\cdots +t_k \vec u_k, \]

kde \(t_1\), \(t_2\), \(\dots\), \(t_k\) jsou nějaká reálná čísla, se nazývá lineární kombinace vektorů \(\vec u_1\), \(\vec u_2\), \(\dots\), \(\vec u_k\). Čísla \(t_1\), \(t_2\), \(\dots\), \(t_k\) nazýváme koeficienty lineární kombinace.

Definice (Lineární závislost a nezávislost)

Řekneme, že vektory \(\vec u_1\), \(\vec u_2\), \(\dots\), \(\vec u_k\) jsou lineárně závislé, jestliže existuje alespoň jedna netriviální lineární kombinace těchto vektorů, jejímž výsledkem je nulový vektor \(\vec o\), tj. existují-li reálná čísla \(t_1\), \(t_2\), \(\dots\), \(t_k\), z nichž alespoň jedno je různé od nuly, taková, že platí

\[ \vec o=t_1\vec u_1+t_2\vec u_2+\cdots +t_k \vec u_k. \]

V opačném případě říkáme, že vektory jsou lineárně nezávislé.

Bude-li z kontextu zřejmé, že proměnná je vektorem, budeme pro pohodlí šipku nad písmenem označujícím jméno proměnné vynechávat.

6.3. Matice

Definice (Matice)

Maticí řádu \(m\times n\) rozumíme schema

\[A=\begin{pmatrix}a_{11}& a_{12}& a_{13}& \cdots{}& a_{1n}\\a_{21}& a_{22}& a_{23}& \cdots{}& a_{2n}\\\vdots{}& \vdots{}& {}& \ddots{}& \vdots{}\\a_{m1}& a_{m2}& \cdots{}& \cdots{}& a_{mn}\end{pmatrix}\]

kde \(a_{ij}\) pro \(i=1..m\) a \(j=1..n\) jsou reálná čísla nebo funkce. Množinu všech matic řádu \(m\times n\), jejichž prvky jsou reálná čísla, označujeme symbolem \(\mathbb R^{m\times n}\). Zkráceně zapisujeme též \({A=(a_{ij})}\).

Je-li \(m=n\) nazývá se matice \(A\) čtvercová matice, jinak obdélníková matice. Je-li \(A\) čtvercová matice, nazýváme prvky tvaru \(a_{ii}\), tj. prvky, jejichž řádkový a sloupcový index jsou stejné, prvky hlavní diagonály.

Matice, která vznikne tak, že její řádky jsou tvořeny sloupci matice \(A\) se nazývá matice transponovaná k matici \(A\) a označuje \(A^T\).

Pro matice definujeme sčítání a násobení číslem stejně jako u vektorů, tj. po složkách. Tyto operace přirozeně přebírají všechny důležité vlastnosti operace sčítání, jako jsou asociativita, komutativita, existence neutrálního prvku nebo existence opačného prvku.

V této fázi je vlastně jedno, jestli prvky jsou uspořádány jako řádkový nebo sloupcový vektor nebo jako matice. Odlišení matic a vektorů provedeme zavedením maticového součinu.

Definice (Součin matic)

Buďte \(A=(a_{ij})\) matice řádu \(m\times n\) a \(B=(b_{ij})\) matice řádu \(n\times p\). Součinem matic \(A\) a \(B\) (v tomto pořadí) rozumíme matici \(G=(g_{ij})\) řádu \(m\times p\), kde

\[ g_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj} \]

pro všechna \(i=1..m\), \(j=1..p\). Zapisujeme

\[{G=AB}\]

(v tomto pořadí).

Slovy: v \(j\)-tém sloupci matice \(AB\) je lineární kombinace sloupců matice \(A\), přičemž koeficienty této lineární kombinace jsou prvky z \(j\)-tého sloupce matice \(B\).

Vztah pro maticový součin se také často zapisuje symbolicky

\[ g_{ik} = \sum_{j=1}^N a_{ij}b_{jk}\]

nebo zkráceně

\[ g_{ik} = a_{ij}b_{jk},\]

kde platí konvence, že pokud se nějaký index opakuje, potom se přes něj sčítá (Einsteinova sumační konvence). V tomto případě se vpravo opakuje index \(j\) a proto se pravé strana sčítá přes všechny hodnoty tohoto indexu.

Na maticový součin můžeme pohlížet i pomocí pojmů známých z analytické geometrie. Prvky v součinu matic jsou skalárními součiny řádků první matice se sloupci druhé matice.

Maticový součin má následující vlastnosti

• je asociativní

  \[(AB)C=A(BC)=ABC,\]

• je distributivní vzhledem ke sčítání

  \[A(B+C)=AB+AC\qquad \text {a}\qquad (B+C)A=BA+CA,\]

• není však komutativní (\(AB\) je obecně různé od \(BA\), proto v předchozím máme roznásobování závorky zleva i zprava),

• ale při násobení skalárem komutativní je:

  \[A(\lambda B)=\lambda (AB),\]
  kde \(\lambda\) je reálné číslo a \(A\) a \(B\) jsou matice.

Můžeme tedy měnit uzávorkování, můžeme roznásobovat závorky, nesmíme však měnit pořadí matic při násobení.

6.4. Jednotková matice a matice inverzní

V tomto pododdíle si představíme maticovou obdobu jedničky jako neutrálního prvku vzhledem k násobení a převrácené hodnoty.

Definice (Jednotková matice)

Jednotková matice je čtvercová matice mající v hlavní diagonále jedničky a mimo hlavní diagonálu nuly. Značí se \(I\).

Věta (Jednotková matice je neutrálním prvkem vzhledem k násobení)

Jednotková matice splňuje \(AI=A\) a \(IB=B\) pro libovolné matice \(A\) a \(B\), pro které je součin definován.

Převrácená hodnota je definována tak, že součin čísla a jeho převrácené hodnoty je roven jedné. Maticová obdoba tohoto vztahu je v následující definici.

Definice (Inverzní matice)

Inverzní matice ke čtvercové matici \(A\) je matice \(A^{-1}\) splňující

\[A A^{-1}=A^{-1}A=I.\]

6.5. Matice jako zobrazení

Součin matice a vektoru je možno chápat jako zobrazení, které vektor zobrazuje na vektor. Vektorem bývá kvantitativní charakteristika populace v nějakém roce (rozebereme níže) a obrazem vektoru charakteristika v následujícím roce. Tímto způsobem je možné stav v jednom roce projektovat na stav v roce následujícím a proto se v tomto kontextu matice použitá v součinu nazývá matice projekce.

6.6. Vlastní čísla a směry

U zobrazování vektorů pomocí maticového násobení nás velice zajímá, které směry se zachovávají, tj. kdy bude obrazem vektoru jeho násobek.

Definice (Vlastní vektor a vlastní hodnota matice)

Řekneme, že nenulový vektor \(\vec u\) je (pravým) vlastním vektorem matice \(A\) příslušným vlastní hodnotě \(\lambda\), jestliže platí

\[A \vec u=\lambda \vec u.\]

Vlastní čísla se nazývají též vlastní hodnoty matice. Každý nenulový vlastní násobek vlastního vektoru je vlastní vektor příslušný téže vlastní hodnotě.

Kromě pravých vlastních vektorů někdy uvažujeme i levé vlastní vektory, definované rovností

\[ \vec v A = \lambda \vec v\]

a v tomto případě je vektor \(\vec v\) nutno chápat jako řádkový vektor.

Inverze matice, jejíž sloupce jsou tvořeny vlastními (pravými) vektory, má v řádcích vlastní levé vektory.

S vlastními směry se setkáme při hledání stabilních poměrů věkových skupin u věkově strukturované populace a při hledání řešení speciálních soustav lineárních rovnic, při hledání řešení autonomních systémů.

6.7. Markovův řetězec, model skladby lesa

Markovův řetězec je jeden z nejjednodušších modelů popisujících systém, který se může nacházet v různých stavech a mezi těmito stavy se náhodně přepíná podle předem daných pravděpodobností. Pro jeho popis je vhodný matematický aparát založený na teorii matic. Následující ukázka aplikace při studiu populací je z [3].

Americký vědec H. S. Horn studoval druhovou skladbu lesa a vycházel z předpokladů, že existuje konstantní pravděpodobnost, že určitý druh je nahrazen jiným druhem. Tabulka pravděpodobností je níže. Pro každý současný druh jsou v řádku pravděpodobnosti, že tento druh bude za 50 let nahrazen druhem ze záhlaví příslušného sloupce. Například pravděpodobnost toho, že na stanovišti, kde nyní roste bříza topololistá poroste za 50 let červený javor je 50% (první řádek, třetí sloupec). Pravděpodobnost toho, že na stanovišti, kde nyní roste javor za 50 let poroste bříza je nulová (třetí řádek, první sloupec). Model předpokládá, že i když se dřevina v lokalitě nevyskytuje, existuje zdroj semen a dřevina se na této lokalitě může objevit.

	Bříza topololistá	Tupela lesní	Javor červený	Buk
Bříza topololistá	0.05	0.36	0.50	0.09
Tupela lesní	0.01	0.57	0.25	0.17
Javor červený	0.00	0.14	0.55	0.31
Buk	0.00	0.01	0.03	0.96

Procentuální zastoupení jednotlivých druhů budeme charakterizovat vektorem, kde hodnoty pro stromy budou ve stejném pořadí, jako jsou stromy seřazeny v naší tabulce. Pokud například je zastoupena napůl bříza a buk, odpovídá to vektoru \(v(0) = (50,0,0,50)^T.\)

Procentuální zastoupení každého druhu se bude měnit z období na období. Například procentuální zastoupení javoru v dalším období bude dáno procentuálním zastoupením javoru v současnosti a pravděpodobností, že se na stanovišti udrží a dále procentuálním zastoupením ostatních dřevin a pravděpodobností, že tato dřevina bude nahrazena javorem. Tedy pro javor a vektor procentuálního zastoupení \(v = (v_1,v_2,v_3,v_4)^T\) to bude

\[ 0.50 v_1 + 0.25v_2 + 0.55 v_3 + 0.03 v_4 \]

Při použití maticového součinu vektoru rozložení zastoupení s maticí pravděpodobností

\[M=\begin{pmatrix} 0.05 & 0.01 & 0 & 0\cr 0.36& 0.57& 0.14&0.01\cr 0.50&0.25&0.55&0.03\cr 0.09&0.17&0.31&0.96 \end{pmatrix}\]

je zastoupení dřevin v následujícím období dáno vzorcem

\[v(k+1)=Mv(k).\]

Show code cell source Hide code cell source

M = np.matrix([0.05, 0.36, 0.50, 0.09,
              0.01, 0.57, 0.25, 0.17,
              0.0,0.14,0.55,0.31,
              0.0,0.01,0.03,0.96]).reshape(4,4).T
M

matrix([[0.05, 0.01, 0.  , 0.  ],
        [0.36, 0.57, 0.14, 0.01],
        [0.5 , 0.25, 0.55, 0.03],
        [0.09, 0.17, 0.31, 0.96]])

Zkusíme si namodelovat 20 období, tj. tisíc let vývoje. K tomu si připravíme pole do kterého budeme ukládat data. Výchozím stavem bude rovnoměrné zastoupení všech druhů. Vývoj jednotlivých dřevin zachytíme graficky.

Show code cell source Hide code cell source

N = 20
X_init = [25, 25, 25, 25]

X = np.zeros((4, N))
X[:, 0] = X_init
for i in range(N - 1):
    X[:, i + 1] = M @ X[:, i]

t = np.array(range(N))*50
df = pd.DataFrame(
    data = X.T, 
    columns = ["Bříza topololistá", "Tupela lesní", "Javor červený", "Buk"],
    index = t, 
)
df.index.name = "čas/rok"
df.columns.name = "Dominantní dřevina"
df.plot(title="Vývoj procentuálního zastoupení jednotlivých druhů", grid=True)

<Axes: title={'center': 'Vývoj procentuálního zastoupení jednotlivých druhů'}, xlabel='čas/rok'>

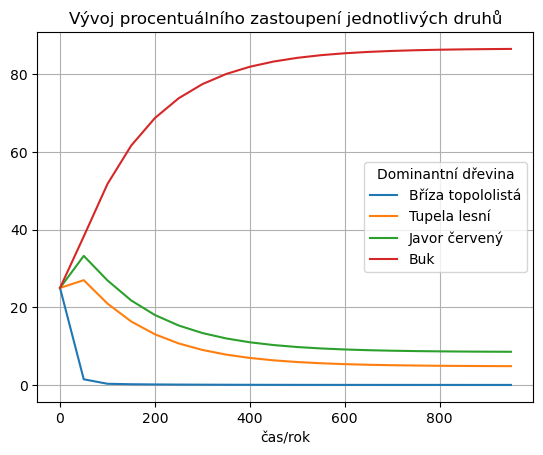
Ze simulace se zdá, že poměr dřevin se postupně stabilizuje. Z matematického hlediska se procentuální zastoupení dřevin nemění, pokud je vektor zastoupení dřevin vlastním vektorem matice příslušným vlastní hodnotě \(1\). Ověříme, že to tak opravdu je.

Show code cell source Hide code cell source

X_final = X[:, [-1]]
print(X_final.ravel())  # array se převede na 1D pomocí ravel
print((M @ X_final).ravel())

[ 0.0516464   4.88304501  8.57619685 86.48911173]
[[ 0.05141277  4.86748704  8.55816607 86.52293412]]

Pokud bychom chtěli simulaci ne po 50 letech, ale po 100 letech, můžeme maticí vynásobit dvakrát. To je v konečném důsledku stejné, jako bychom násobili druhou mocninou. Pokud bychom chtěli delší časový interval, použijeme vyšší mocninu. Následující výpočet ukazuje, že pro dostatečně velkou mocninu vychází všechny sloupce matice stejné a jsou rovny výslednému poměru mezi jednotlivými dřevinami.

Show code cell source Hide code cell source

M**50

matrix([[0.00050824, 0.00050824, 0.00050824, 0.00050824],
        [0.04828282, 0.04828282, 0.04828281, 0.04828279],
        [0.0851273 , 0.0851273 , 0.08512728, 0.08512726],
        [0.86608164, 0.86608164, 0.86608167, 0.86608171]])

Další uplatnění Markovových řetězců je například při předpovědi počasí a jejím zpřesněním na lokální úroveň. Používá informace o tom, s jakou pravděpodobností je jeden druh počasí zachován či vystřídán druhým.

6.8. Leslieho model růstu populace s věkovou strukturou

Britský ekolog Patrick H. Leslie použil maticový součin v roce 1945 k formulaci modelu, sledujícího růst populace s definovanou věkovou strukturou. Model sleduje růst jednotlivých věkových skupin a přechod jedinců z jedné skupiny do druhé.

Model vysvětluje, proč se v populaci ustálí věkové složení na konstantních poměrech. Jedná se o model populární a úspěšný v ekologii a modelování populací, včetně populace lidské.

Model předpokládá, že populace je rozdělena do několika věkových kategorií a v každé kategorii je dána pravděpodobnost dožití se do další kategorie a průměrný počet potomků. Kromě toho je dán pro každou věkovou kategorii průměrný počet potomků připadajících na jednotlivce. Protože potomky rodí samice, byl tento model navržen a je zpravidla uvažován pro modelování počtu samic. Model je však možno adaptovat i na celou populaci, tj. nerozlišovat samce a samice.

Označíme-li pro populaci rozdělenou do tří věkových kategorií \(x_1\) (nejmladší) až \(x_3\) (nejstarší) průměrný počet potomků na jednotlivce (případně potomků samičího pohlaví) během časové jednotky hodnotami \(f_1\) až \(f_3\), je v dalším časovém okamžiku počet jedinců nejnižší kategorie dán výrazem

\[ f_1 x_1 + f_2 x_2+f_3 x_3.\]

Je-li \(p_1\) pravděpodobnost přežití členů nejmladší kategorie a jejich postupu do vyšší věkové třídy, je velikost populace v druhé věkové třídě dána výrazem

\[ p_1 x_1.\]

Podobně postupujeme při přechodu z prostřední do nejstarší kategorie. Zapsáno modelem i s explicitním uvedením času jako argumentu máme

\[ \begin{aligned} x_1(k+1) &= f_1 x_1(k) + f_2 x_2(k) +f_3 x_3(k)\\ x_2(k+1) &=p_1 x_1(k)\\ x_3(k+1) &=p_2 x_2(k) \end{aligned} \]

anebo (zapsáno jednou maticovou rovnicí)

\[\begin{pmatrix} x_1(k+1) \\ x_2(k+1) \\ x_3 (k+1) \end{pmatrix} = \begin {pmatrix} f_1 & f_2 & f_3 \\ p_1 & 0 & 0\\ 0 & p_2 & 0 \end{pmatrix} \begin{pmatrix} x_1(k) \\ x_2(k) \\ x_3 (k) \end{pmatrix}.\]

Opakovaným násobením získáme věkovou strukturu populace v další generaci a toto se opakuje podobně jako u Markovova řetězce.

Při použití modelu volíme časový interval odpovídající jednotlivým stadiím dostatečně krátký tak, aby v prvním řádku byly alespoň dvě po sobě jdoucí hodnoty kladné. Potom má Leslieho matice následující vlastnosti.

• Matice má jednu kladnou vlastní hodnotu \(\lambda_1\), která je dominantní v tom smyslu, že všechny ostatní vlastní hodnoty jsou v absolutní hodnotě menší.

• Dominantní vlastní hodnota určuje rychlost růstu populace v dlouhodobém měřítku.

  • Je-li dominantní vlastní hodnota rovna jedné, populace se v dlouhodobém měřítku stabilizuje a její velikost se ustálí na stavu, kdy dále neroste ani neklesá.

  • Je-li dominantní vlastní hodnota větší než jedna, velikost populace setrvale roste geometrickou řadou s kvocientem daným touto vlastní hodnotou.

  • Je-li dominantní vlastní hodnota mezi nulou a jedničkou, velikost populace klesá geometrickou řadou.

• Vektor příslušný dominantní vlastní hodnotě určuje rozložení populace do jednotlivých věkových tříd poté, co se toto rozložení ustálí.

6.9. Zobecnění Leslieho modelu

6.9.1. Agregace nejstarších věkových kategorií

Pro praktické využití Leslieho modelu je někdy vhodné redukovat počet uvažovaných věkových tříd tak, že nejstarší věkové třídy shrneme do třídy jediné. Poté tedy členové nejstarší věkové třídy automaticky v dalším časovém kroku nevymírají, ale určité procento jich pouze zestárne a zůstávají ve své nejstarší kategorii. V Leslieho matici se toto projeví tak, že prvek v pravém dolním rohu matice je nenulový.

6.9.1.1. Model populace tuleňů

Následující příklad je z [13].

Populace samiček tuleňů je rozdělena na tři třídy: mláďata (0 až 4 roky), mladé tuleně (4 až 8 let) a dospělé tuleně (nad 8 let). Jednotka času budou 4 roky. Mláďata do čtyř let nemají potomky. Mladí tuleni mají průměrně \(1.26\) a dospělí průměrně \(2.0\) samičích potomků každé 4 roky. Mláďata dorostou do další věkové kategorie (tj. nezahynou) s pravděpodobností 0.614, mladí tuleni dorostou do kategorie dospělých s pravděpodobností 0.808 a pravděpodobnost, že starý tuleň přežije další 4 roky je také 0.808.

Model může být reprezentován rekurentním vztahem

\[\begin{pmatrix} x_1(k+1) \\ x_2(k+1) \\ x_3 (k+1) \end{pmatrix} = \begin {pmatrix} 0 &1.26&2.0\cr 0.614&0&0&\cr 0&0.808&0.808 \end{pmatrix} \begin{pmatrix} x_1(k) \\ x_2(k) \\ x_3 (k) \end{pmatrix}.\]

Matice \(L=\begin {pmatrix} 0 &1.26&2.0\cr 0.614&0&0&\cr 0&0.808&0.808 \end{pmatrix}\) má jediné reálné kladné vlastní číslo a toto vlastní číslo je větší než 1.

Show code cell source Hide code cell source

L = np.matrix([
    0, 1.26, 2.0,
    0.614, 0, 0,
    0, 0.808, 0.808
]).reshape(3,3)
print(L,"\n")
v,P = np.linalg.eig(L)
print("Vlastní hodnoty: ",v)
print("Vlastní vektory jsou sloupce matice\n",P,"\n")

vh,vs = [ [i.real,j.real] for i,j in zip(v,P.T) if np.abs(i.imag)<1e-2 ][0]
vs = vs.A1 # převod matice na vektor
vs = vs/sum(vs) # normování aby součet komponent byl jedna
print("Reálná vlastní hodnota je ", vh)
print("Příslušný vlastní směr je", vs)

[[0.    1.26  2.   ]
 [0.614 0.    0.   ]
 [0.    0.808 0.808]] 

Vlastní hodnoty:  [-0.34182332+0.35954975j -0.34182332-0.35954975j  1.49164663+0.j        ]
Vlastní vektory jsou sloupce matice
 [[ 0.38392628-0.40383611j  0.38392628+0.40383611j  0.84331389+0.j        ]
 [-0.68962744+0.j         -0.68962744-0.j          0.34712962+0.j        ]
 [ 0.44144739+0.1380406j   0.44144739-0.1380406j   0.4102715 +0.j        ]] 

Reálná vlastní hodnota je  1.4916466348833581
Příslušný vlastní směr je [0.52683575 0.2168591  0.25630515]

Časový vývoj modelu z počátečního stavu \([10,5,12]\) po dobu deseti jednotek času (tj. 40 let) je zachycen na následujícím obrázku.

Show code cell source Hide code cell source

N = 10
X = np.zeros((3,N+1))
X[:,0] = [10,5,12]
for i in range(N):
    X[:,i+1] = L@X[:,i]

df = pd.DataFrame(data=X.T, 
                  columns=["mláďata","mladí tuleni","staří tuleni"], 
                  index=4*np.arange(0,X.shape[1])
                 )
df.index.name = "čas/rok"
df.columns.name = "věková kategorie"    
df.plot(grid=True, title="Vývoj počtu tuleňů", ylabel="počet jedinců");

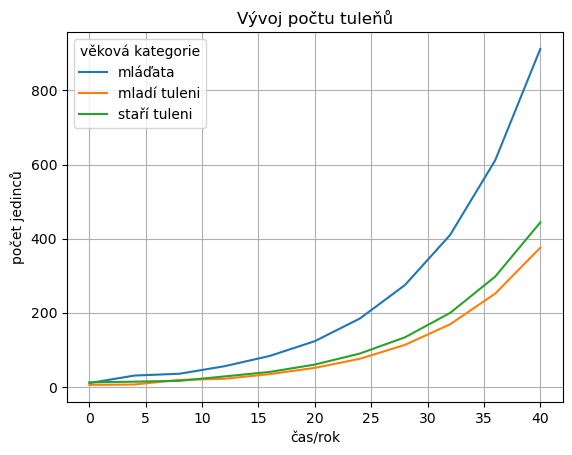
Tip

Rychlost exponenciálního růstu se nejlépe posuzuje na grafu, kde svislá komponenta je logaritmická. Zkuste graf překreslit s novým nastavením, tj. vynechat omezení pro svislou osu a použít pro ni logaritmickou škálu. V takovém grafu má exponenciální funkce tvar přímky a ze vzájemné polohy přímek snadno poznáme, jestli všechny věkové kategorie rostou stejně rychle.

Pokud převedeme absolutní čísla na podíly z celku, získáme vývoj věkové skladby populace.

Show code cell source Hide code cell source

podil = df.div(df.sum(axis=1), axis=0).mul(100)
podil.plot(
        title="Procentuální zastoupení kategorií", 
        ylabel="procento z celkového počtu", 
        grid=True);

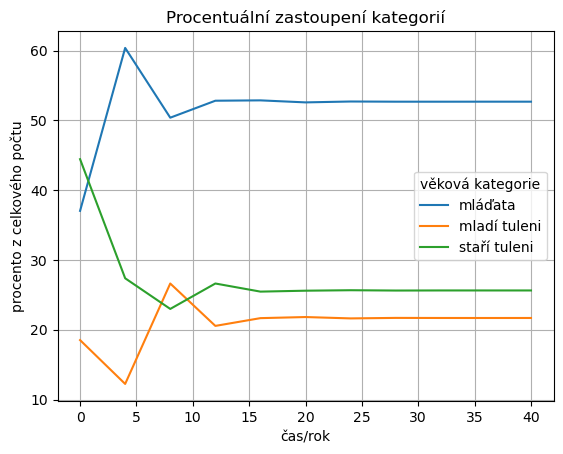
Procentuální skladba populace, ke které vývoj konverguje, je přibližně dána poslední položkou.

Show code cell source Hide code cell source

podil.iloc[-1,:]

věková kategorie
mláďata         52.683290
mladí tuleni    21.686628
staří tuleni    25.630082
Name: 40, dtype: float64

6.9.2. Lefkovitchův model

Anglický biolog L.P. Lefkovitch představil model analogický Leslieho modelu, ale namísto s věkovými kategoriemi model pracuje s vývojovými stadii. To je pro některé druhy přirozenější. Například rostliny v nepříznivých podmínkách mohou růst pomaleji a věk není spolehlivým prediktorem dalšího vývoje. Model je podobný Leslieho modelu s tím, že je jiná interpretace jednotlivých kategorií (nejedná se o věkové třídy, ale o vývojová stadia) a matice modelující chování takového systému může mít na rozdíl od Leslieho matice nenulové prvky i v hlavní diagonále.

U živočichů se tento model může používat v situacích, kdy jednotlivé fáze života nejsou stejně dlouhé, například u želv (Crouse, Crowder, Caswell: A stage-based population model for loggerhead sea turtles and implications for conservation, Ecology, 68(5), 1987, pp. 1412-1423, http://web.abo.fi/fak/mnf/mate/kurser/matriser/Turtlearticle.pdf). Dále se používá v případě, že je obtížné nebo neefektivní stanovit věk jednotlivců nebo v případě, kdy někteří jedinci vykazují zrychlený či zpomalený růst.

Zobecnění Leslieho matice uvedené v předchozí podkapitole je vlastně speciálním případem Lefkovitchova modelu.

6.9.3. Usherův model

S modifikací podobnou Lefkovitchově modelu přišel britský biolog Michael B. Usher. Namísto vývojových stadií použil jako prediktor dalšího vývoje velikost. To je vhodné pro některé rostliny, například pro stromy.

Společným znakem všech dosud uvedených modelů (Markov, Leslie, Lefkovitch, Usher) je, že matice je použita jako nástroj projektující současný stav populace na situaci po uplynutí jedné časové jednotky.

6.10. Soustavy lineárních rovnic

Uvažujme soustavu lineárních rovnic

(6.1)\[ \begin{aligned} a_{11} x_1+a_{12}x_2 &=b_1,\cr a_{21}x_1+a_{22}x_2&=b_2. \end{aligned} \]

Tuto soustavu je možné zapsat jako jednu vektorovou rovnici ve tvaru

\[ \begin{pmatrix} a_{11}\cr a_{21}\end{pmatrix} x_1 +\begin{pmatrix} a_{21}\cr a_{22}\end{pmatrix} x_2 = \begin{pmatrix} b_{1}\cr b_{2}\end{pmatrix} \]

anebo pomocí maticového součinu ve tvaru

\[ \begin{pmatrix} a_{11} & a_{12}\cr a_{21} & a_{22}\end{pmatrix} \begin{pmatrix} x_{1}\cr x_{2}\end {pmatrix} = \begin{pmatrix} b_{1}\cr b_{2}\end{pmatrix}. \]

Označíme-li matice v tomto vztahu postupně \(A\), \(X\) a \(B\), potom soustavu (6.1) je možno zapsat ve tvaru

\[AX=B.\]

Tuto možnost je pochopitelně možno použít pro libovolný počet rovnic a neznámých. Maticový součin umožňuje snadno zapsat a pracovat se soustavami lineárních rovnic.

6.11. Lineární autonomní systémy

Lineární autonomní systémy jsou soustavy ve tvaru

\[\frac{\mathrm dX}{\mathrm dt}=AX+B,\]

kde \(X\) je neznámá vektorová funkce, \(B\) je vektor a \(A\) je čtvercová matice.

Je-li dimenze vektorů malá, bývá zvykem systém rozepsat do komponent. Například ve dvoudimenzionálním případě by tento zápis byl ekvivalentní dvojici rovnic

\[ \begin{aligned} \frac{\mathrm dx_1}{\mathrm dt} & = a_{11}x_1+a_{12}x_2 + b_1, \cr \frac{\mathrm dx_2}{\mathrm dt} & = a_{21}x_1+a_{22}x_2 + b_2. \end{aligned} \]

S takovými soustavami se setkáme při studiu interagujících populací. Výhodou lineárních autonomními systémů je, že pomocí vlastních čísel a vlastních vektorů můžeme napsat přímo jejich řešení. Nevýhodou je, že reálné děje jsou komplikovanější, než je podchytitelné lineárními rovnicemi a jejich soustavami. Neznamená to však, že lineární rovnice a soustavy rovnic nevyužijeme. Využívá se jich naopak velmi často. Jsou to totiž jediné soustavy diferenciálních rovnic, které umíme vyřešit. Proto se na ně spoléháme i při práci s nelineárními modely. Princip práce v takovém případě spočívá v tom, že vytipujeme body našeho zájmu v nich aproximujeme nelineární model modelem lineárním. Poté vyřešíme lineární model a nakonec informace o řešení přeneseme na model nelineární.