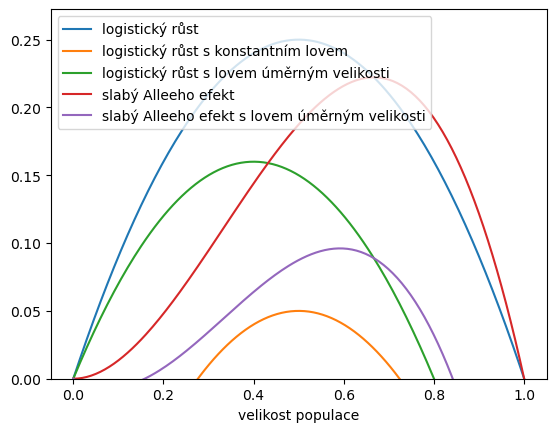
3. Lov v populaci - fázový portrét

Model

\[\frac{\mathrm dx}{\mathrm dt}=rx^{1+a}\left(1-\frac xK\right)-h-Hx\]

v závislosti na parametrech zahrnuje logistický růst, slabý Alleeho efekt (pro \(a\neq 0\)), lov konstantní intenzity (pro \(h\neq 0\)) anebo lov s konstatnním úsilím (pro \(H\neq 0\)).

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

def model(x,r=1,K=1,h=0, a=0, H=0):
    return r*(x**(1+a))*(1-x/K)-h-H*x

parametry =[ 
[{},"logistický růst"],
[{'h':0.2},"logistický růst s konstantním lovem"],
[{'H':0.2},"logistický růst s lovem úměrným velikosti"],
[{'a':1, 'r':1.5},"slabý Alleeho efekt"],
[{'a':1, 'r':1.5, 'H':0.2},"slabý Alleeho efekt s lovem úměrným velikosti"]
]

x = np.linspace(0,1,200)
df = pd.DataFrame(index=x)
df.index.name = "velikost populace"

for data,popis in parametry:
    df[popis] = model(x,**data)
df

	logistický růst	logistický růst s konstantním lovem	logistický růst s lovem úměrným velikosti	slabý Alleeho efekt	slabý Alleeho efekt s lovem úměrným velikosti
velikost populace
0.000000	0.000000	-0.200000	0.000000	0.000000	0.000000
0.005025	0.005000	-0.195000	0.003995	0.000038	-0.000967
0.010050	0.009949	-0.190051	0.007939	0.000150	-0.001860
0.015075	0.014848	-0.185152	0.011833	0.000336	-0.002679
0.020101	0.019696	-0.180304	0.015676	0.000594	-0.003426
...	...	...	...	...	...
0.979899	0.019696	-0.180304	-0.176283	0.028951	-0.167029
0.984925	0.014848	-0.185152	-0.182137	0.021936	-0.175049
0.989950	0.009949	-0.190051	-0.188041	0.014774	-0.183216
0.994975	0.005000	-0.195000	-0.193995	0.007462	-0.191533
1.000000	0.000000	-0.200000	-0.200000	0.000000	-0.200000

200 rows × 5 columns

ax = df.plot()
ax.set(ylim=(0,None));

# Export do Excelu
df.to_excel('data.xlsx')

3.1. Cvičení

Zkopírujte si buňky výše a pokuste se modifikovat kód tak, aby nakreslil pravou stranu logistické rovnice, poté totéž pro nosnou kapacitu navýšenou o 50 procent a do třetice totéž, ale o 50 procent bude navýšen parametr \(r\). Jediné, co musíte provést, je modifikovat seznam v proměnné parametry.