2. Diferenciální rovnice

import numpy as np
import pandas  as pd
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

2.1. Řešení rovnice a vizualizace řešení.

Rychlost růstu populace o velikosti \(N\) v lokalitě s nosnou kapacitou \(K\) je možno popsat diferenciální rovnicí

\[\frac{\mathrm dN}{\mathrm dt}=rN\left(1-\frac NK\right), \]

kde \(r\) je rychlost růstu populace bez započtení vnitrodruhové konkurence.

### Příprava funkcí a parametrů
pocatecni_podminky = [0.1,0.5,1.5]  # počáteční podmínka nebo podmínky
meze = [0,15]  # interval, na kterém hledáme řešení
n = 100 # počet bodů, ve kterých budeme počítat řešení

def model(t, N):
    """
    Funkce definující rychlost růstu.
    """
    r = 1
    K = 1
    return  r*N*(1-N/K)

### Řešení modelu
t=np.linspace(*meze, n)  # definiční obor, v těchto bodech budeme hledat řešení
reseni = solve_ivp(
                   model,
                   meze,
                   pocatecni_podminky,
                   t_eval=t
                   )

### Vizualizace řešení
fig,ax = plt.subplots(1)
ax.plot(t,reseni.y.T)
ax.set(
    ylim = (0,None),
    title = "Růst populace",
    xlabel="čas",
    ylabel="velikost populace",
);

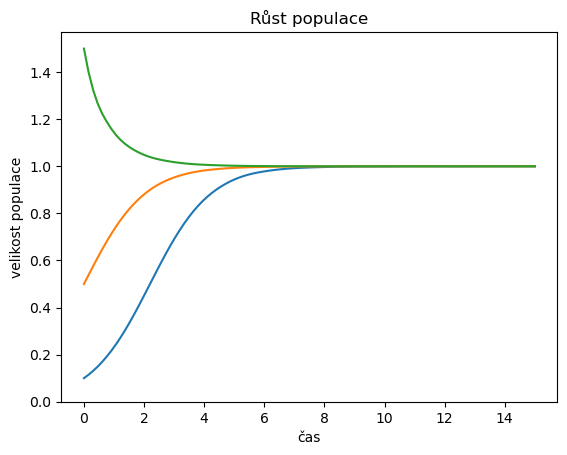
Následující kód vyřeší rovnici

\[\frac{\mathrm dN}{\mathrm dt}= \frac b{D(N+\beta)}-a\frac {N^k}S\]

dynamické rovnováhy na ostrově s nulovou počáteční podmínkou.

2.1.1. Úkoly:

• Vyzkoušejte si. Zkuste i zadání více počátečních podmínek, například řádek pocatecni_podminka = [0] vyměňte za pocatecni_podminka = [0,5,10,20]. Tím získáte řešení pro několik počátečních podmínek současně.

• Vykopírujte text do nové buňky a opravte tak, aby zobrazoval řešení počáteční úlohy

  \[\frac{\mathrm dT}{\mathrm dt}=-0.1(T-20), \quad T(0)=100\]
  s ochlazováním kávy. I zde zkuste více počátečních podmínek.

### Příprava funkcí a parametrů
pocatecni_podminka = [0]  # počáteční podmínka nebo podmínky
meze = [0,15]  # interval, na kterém hledáme řešení
n = 100 # počet dělících bodů

def model(t, N, a=1, b=8, beta=0.2, D=0.5, k=1.3, S=20):
    """
    Funkce z pravé strany modelu dynamické rovnováhy počtu druhů na ostrovech, 
    podle McArthura a Wilsona. 
    
    Vstup:
    -----
    Povinnými parametry jsou čas a počet druhů, volitelnými vzdálenost 
    D od pevniny, rozloha ostrova S, další parametry modelu a konstanty 
    úměrnosti. Přednastavené hodnoty jsou pouze ilustrační, závisí na volbě
    jednotek a konkrétním použití.
    
    Výstup:
    ------
    Hodnota funkce.
    """
    kolonizace = b/(D*(N+beta))
    vymirani = a*N**k/S 
    return  kolonizace - vymirani 

### Řešení modelu
t=np.linspace(*meze, n)  # definiční obor, v těchto bodech budeme hledat řešení
reseni = solve_ivp(
                   model,
                   meze,
                   pocatecni_podminka,
                   t_eval=t
                   )

### Vizualizace řešení
fig,ax = plt.subplots(1)
ax.plot(t,reseni.y.T)
ax.set(
    ylim = (0,None),
    title = "Dynamická rovnováha počtu druhů na ostrově",
    xlabel="čas",
    ylabel="počet druhů",
);

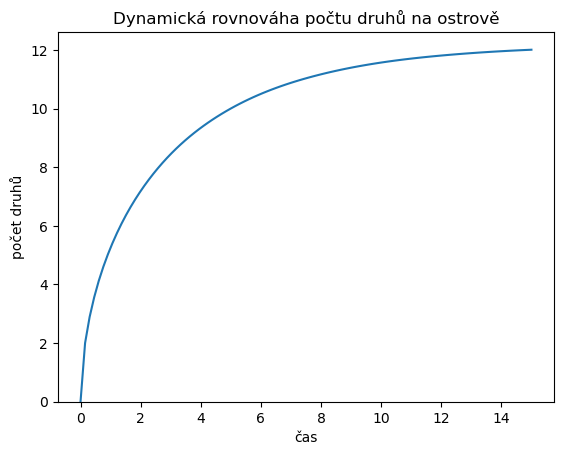
2.2. Řešení pro sadu parametrů

Následující kód řeší vícekrát rovnici dynamické rovnováhy pro několik různých vzdálenosti ostrova od pevniny.

V čem se kód změnil od předchozího? Prohlédněgte si diff obou kódů.

• Používá se proměnná se seznamem parametrů.

• Data se ukládají do tabulky, protože místo jednoho řešení budeme mít řešení několik.

• Ve volání příkazu solve_ivp se předává hodnota parametru.

• Příkazy pro řešení rovnice a uložení do tabulky jsou volány v cyklu.

• Pro kreslení se dá použít metoda plot pro tabulky.

### Příprava funkcí a parametrů
pocatecni_podminka = [0]  # počáteční podmínka
meze = [0,15]  # interval, na kterém hledáme řešení
n = 100 # počet dělících bodů
parametry = [0.25,0.5,1,2] # seznam parametrů


def model(t, N, a=1, b=8, beta=0.2, D=0.5, k=1.3, S=20):
    """
    Funkce z pravé strany modelu dynamické rovnováhy počtu druhů na ostrovech, 
    podle McArthura a Wilsona. 
    
    Vstup:
    -----
    Povinnými parametry jsou čas a počet druhů, volitelnými vzdálenost 
    D od pevniny, rozloha ostrova S, další parametry modelu a konstanty 
    úměrnosti. Přednastavené hodnoty jsou pouze ilustrační, závisí na volbě
    jednotek a konkrétním použití.
    
    Výstup:
    ------
    Hodnota funkce.
    """
    kolonizace = b/(D*(N+beta))
    vymirani = a*N**k/S 
    return  kolonizace - vymirani 

### Řešení modelu
t=np.linspace(*meze, n)  # definiční obor, v těchto bodech budeme hledat řešení
df = pd.DataFrame(index=t, columns=parametry)      # tabulka pro výstup

for parametr in parametry:
    reseni = solve_ivp(
                       lambda t,x:model(t,x,D=parametr),
                       meze,
                       pocatecni_podminka,
                       t_eval=t
                       )
    df[parametr] = reseni.y.T # další sloupec tabulky
    # lambda funkce viz https://www.w3schools.com/python/python_lambda.asp
    # (dočasná nepojmenovaná funkce)

### Vizualizace řešení
ax = df.plot()
ax.set(
    ylim = (0,None),
    title = "Dynamická rovnováha počtu druhů na ostrově",
    xlabel="čas",
    ylabel="počet druhů",
)
plt.legend(title="Vzdálenost ostrova");

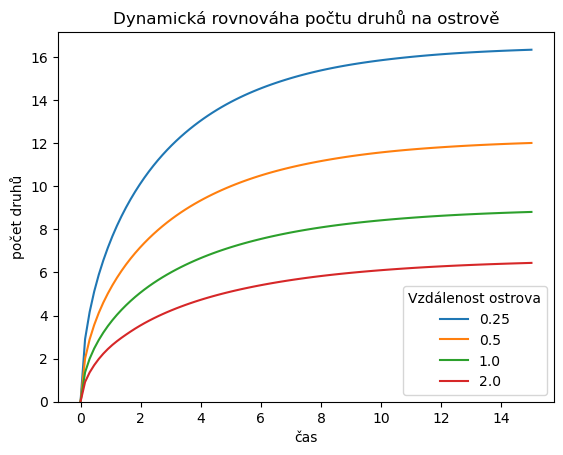
2.2.1. Úkoly

• Vyzkoušejte si kód.

• V nové buňce sledujte vliv rozlohy ostrova (vzdálenost je stejná) na druhovu skladbu. Vykopírujte si kód a proveďte příslušnou modifikaci.

• Před každou buňku s výpočty vložte textovou buňku popisující, co se ve výpočtu odehrává, co se snažíme ukázat. Musíte vložit buňku, změnit typ z Code na Markdown (vybrat buňku a stisknout M, nebo použít rozbalovací menu v toolbaru a vepsat komentář.

• Pokud jsou veličiny \(S\) a \(D\) ve stále stejném poměru, je stejná i hodnota, ke které konverguje řešení (viz přednáška).

  • Znamená to, že se budou populace vyvíjet stejně na daném ostrově a na ostrově, který je dvakrát větší a dvakrát dále? V čem se bude situace lišit a v čem bude stejná?

  • Odhadněte odpověď a potvrďte si hypotézu tak, že budete modelovat plnou diferenciální rovnici pro obě uvažované situace. Můžete použít něco jako lambda t,x:model(t,x,D=0.5*nasobek,S=20*nasobek) a proměnnou nasobek nechat iterovat přes nějaký seznam.

  • Nepodařilo se? Potřebné modifikace jsou zde. (Jedná se o minimální modifikaci řešící úlohu, ještě je ale nutné opravit popisky.)