1. Funkce a vlastnosti funkcí

Co se dozvíte v tomto textu

Při studiu libovolného fenoménu dříve či později skončíme u snahy kvantifikovat velikosti znaků, které nás zajímají a sledovat vztahy mezi jednotlivými znaky. Jinými slovy, sledujeme vybrané veličiny a pomocí funkcí vyjadřujeme vztahy mezi těmito veličinami navzájem, nebo mezi těmito veličinami a parametry prostředí. Typickým případem je sledování velikosti populace a jejího vývoje v čase. Tím je možné odhalit některé děje, jako například periodické kolísání populace rysa a zajíce v okolí Hudsonova zálivu.

V úvodním textu si zopakujeme pojmy potřebné pro práci s funkcemi a v některých částech si pojmy rozšíříme nad úroveň střední školy.

Foto: Rys kanadský (Lynx canadensis). Pravidelné fluktuace populací rysa a zajíce slouží v literatuře k vysvětlení dynamiky společenstva dravce a kořisti. Autor Keith Williams, https://commons.wikimedia.org

Při studiu přírodních dějů a jevů sledujeme vybrané charakteristiky, kterým je možno přiřadit číselné hodnoty spojené s jednotkou. Například velikost populace v kusech jedinců. Takové charakteristiky se nazývají veličiny.

Pokud u dané populace sledujeme více veličin, mohou mezi těmito veličinami být jisté vztahy. Takové vztahy vyjadřujeme pomocí funkcí. Jednou z veličin může být třeba čas v letech a druhou z veličin velikost populace. Funkce potom udává souvislost mezi velikostí populace a časem. Může například jít o vzorec, do kterého dosadíme čas a vzorec nám ukáže velikost populace.

1.1. Funkce jedné proměnné

Formální definice funkce je v následujícím odstavci. Zpravidla nebývá pro pochopení práce s funkcemi nutná a postačí intuitivní chápání tohoto pojmu jako vztahu mezi dvěma veličinami nebo mezi dvěma proměnnými.

Definice (Funkce)

Buďte \(A\) a \(B\) neprázdné podmnožiny množiny reálných čísel. Pravidlo \(f\), které každému prvku množiny \(A\) přiřadí jediný prvek množiny \(B\) se nazývá funkce (přesněji: reálná funkce jedné reálné proměnné). Zapisujeme \(f:A\to B\). Skutečnost, že prvku \(a\in A\) je přiřazen prvek \(b\in B\) zapisujeme \(f(a)=b\). Přitom říkáme, že \(b\) je obrazem prvku \(a\) při zobrazení \(f\), resp. že \(a\) je vzorem prvku \(b\) při zobrazení \(f\).

Hodnoty \(x\), pro které je jejich obraz roven nule, se nazývají kořeny funkce.

Zjednodušeně řečeno, funkce je pravidlo, které zadanému číslu na vstupu dokáže přiřadit pevně definované číslo na výstupu.

Funkce vizualizujeme pomocí grafu v kartézské soustavě souřadnic. Na vodorovnou osu vynášíme vzory, na svislou obrazy. V prakticky zajímavých a využívaných případech zpravidla body grafu vyplní křivku v rovině.

Show code cell source Hide code cell source

import numpy as np  # knihovna pro numerické výpočty
import matplotlib.pyplot as plt  # knihovna pro grafiku
import pandas as pd # knihovna pro práci s tabulkami

Show code cell source Hide code cell source

t = np.linspace(0,4*np.pi,1000)  # interval a počet bodů použitých pro kreslení grafu
y = np.sin(t)  # výpočet funkčních hodnot
plt.plot(t,y)  # vykreslení grafu
plt.show();

1.2. Vlastnosti funkcí

Pro práci s funkcemi si všímáme vlastností, které jsou určitým způsobem vypovídající o tom, jak se funkce chová na definičním oboru nebo na jeho podmnožině. Zajímá nás zejména

• jestli při seřazení vstupních dat podle velikosti jsou výstupy seřazeny stejným způsobem (rostoucí funkce) nebo naopak (klesající funkce),

• jestli výsledek na výstupu funkce jednoznačně determinuje data na vstupu (prostá funkce),

• jak určit data na vstupu z výsledku na výstupu, pokud tato data určit jdou (inverzní funkce),

• jestli data na výstupu funkce nutně zůstávají mezi nějakými pevnými hodnotami (ohraničenost)

• a jestli se funkce pro hodně velká data chovají přibližně stejně jako nějaké jednodušší funkce (asymptotika).

To bylo neformální představení základních vlastností, kterých si všímáme u funkcí. Taková představa většinou stačí. Přesné definice jsou následující.

Definice (Monotonie funkce)

Nechť \(f\) je funkce a \(M\subseteq \mathrm{Dom}(f)\) podmnožina definičního oboru funkce \(f\)

• Řekneme, že funkce \(f\) je na množině \(M\) rostoucí jestliže pro každé \(x_1, x_2\in M\) s vlastností \(x_1<x_2\), platí \(f(x_1)<f(x_2)\).

• Řekneme, že funkce \(f\) je na množině \(M\) klesající jestliže pro každé \(x_1, x_2\in M\) s vlastností \(x_1<x_2\), platí \(f(x_1)>f(x_2)\).

• Řekneme, že funkce \(f\) je na množině \(M\) (ryze) monotonní je-li buď rostoucí, nebo klesající na \(M\).

Nespecifikujeme-li množinu \(M\), máme na mysli, že uvedená vlastnost platí na celém definičním oboru funkce \(f\).

Následující definice zavádí třídu funkcí, u kterých se z výsledku dají zrekonstruovat vstupní data.

Definice (Prostá funkce)

Nechť \(f\) je funkce a \(M\subseteq \mathrm{Dom}(f)\) podmnožina definičního oboru funkce \(f\). Řekneme, že funkce \(f\) je prostá, jestliže každý obraz má jen jediný vzor, tj. pro každé \(y_0\in f(M)\) existuje jediné \(x\in M\) s vlastností \(f(x)=y_0\). Nespecifikujeme-li množinu \(M\), máme na mysli, že uvedená vlastnost platí na celém definičním oboru funkce \(f\).

Následující věta vyjadřuje, že pokud je funkce prostá, je možno ji odebrat z obou stran rovnice a výsledkem je rovnice ekvivalentní.

Věta (Rovnice s prostou funkcí)

Pokud je \(f\) prostá funkce a platí

\[f(x)=f(a),\]

potom platí \(x=a.\)

Pokud je funkce prostá, je možné z výsledku zrekonstruovat vstupní data. Následující definice dává název funkci, která toto přiřazení vstupních dat k výsledkům realizuje.

Definice (Inverzní funkce)

Nechť funkce \(f: A\to B\) je prostá. Pravidlo, které každému \(x\) z množiny \(f(A)\) přiřadí to (jediné) \(y\), pro které platí \(f(y)=x\) se nazývá inverzní funkce k funkci \(f\), označujeme \(f^{-1}\).

Například k druhé odmocnině je inverzní funkcí druhá mocnina. K násobení dvojkou je inverzní funkcí dělení dvojkou.

Definice (Ohraničená funkce)

Funkce se nazývá shora ohraničená na množině \(M\), pokud existuje reálné číslo \(K\) takové, že platí

\[f(x)<K\]

pro všechna \(x\) z množiny \(M\).

Analogicky pomocí opačné nerovnosti definujeme ohraničenost na množině \(M\) zdola.

Funkce je ohraničená na množině \(M\), pokud je ohraničená současně shora i zdola.

Pokud množinu \(M\) vynecháme, máme na mysli ohraničenost na celém maximálním definičním oboru.

Příklad 1.1

Sinus a kosinus jsou ohraničené funkce. Exponenciální funkce je zdola ohraničená a není shora ohraničená. Na intervalu konečné délky je ohraničená i exponenciální funkce.

Definice (Landauova notace)

Nechť \(g\) je funkce kladná pro velká \(x\). Řekneme, že funkce \(f\) je třídy \(\mathcal O(g)\), píšeme

\[f(x)=\mathcal O(g(x)),\]

pokud je funkce \(|f(x)|/g(x)\) ohraničená pro velká \(x\), tj. pokud pro nějakou konstantu \(M\) platí

\[|f(x)|\leq M g(x)\]

pro velká \(x\).

Řekneme, že funkce \(f\) je třídy \(O(g)\) v okolí bodu \(a\), pokud uvedené vztahy platí na nějakém intervalu obsahujícím ve svém vnitřku bod \(a\).

Je-li funkce \(f(x)=O(x^2)\), existuje konstanta \(K\) s vlastností

\[|f(x)|\leq Kx^2\]

pro velká \(x\).

1.3. Elementární funkce

Shrneme si nejdůležitější pojmy spojené s elementárními funkcemi. Jedná se o znalosti ze střední školy a možná jejich mírné rozšíření. Proto není potřeba vždy tyto funkce na současném místě formálně přesně definovat.

1.3.1. Přímá a nepřímá úměrnost

Je to až k nevíře, ale k popisu obrovského množství dějů stačí čtyři základní operace: sčítání, odčítání, násobení a dělení. Vzhledem k požadavku na konzistenci fyzikálních jednotek se nejčastěji setkáváme s násobením a dělením a proto funkce pracující s těmito operacemi mají výsadní postavení. Dokonce si vysloužily pojmenování běžně užívané i mezi nematematiky: přímá a nepřímá úměrnost. Je to formální popis situace, kdy souvislost mezi dvěma veličinami je zprostředkována násobením konstantou (přímá úměrnost), nebo kdy je násobením konstantou zprostředkována souvislost mezi jednou veličinou a převrácenou hodnotou druhé veličiny (nepřímá úměrnost).

Definice (Přímá a nepřímá úměrnost)

Veličina \(y\) je přímo úměrná veličině \(x\) jestliže existuje konstanta \(k\) taková, že platí

\[ y=kx. \]

Veličina \(y\) je nepřímo úměrná veličině \(x\) jestliže existuje konstanta \(k\) taková, že platí

\[y =\frac kx. \]

Je-li veličina \(y\) úměrná veličině \(x\), píšeme \(y\sim x\) nebo \(y\propto x.\) Je-li navíc konstanta úměrnosti blízká jedničce, tj. \(x\) a \(y\) jsou blízké, píšeme \(y\approx x.\)

Pro nepřímou úměrnost píšeme podobně \(y\sim \frac 1x\), \(y\propto \frac 1x\) a \(y\approx \frac 1x\) s využitím toho, že nepřímá úměrnost mezi dvěma veličinami je vlastně přímá úměrnost mezi jednou veličinou a převrácenou hodnotou veličiny druhé.

Grafem přímé úměrnosti je přímka procházející počátkem. Přímá úměrnost může být i klesající, je-li konstanta \(k\) záporná.

1.3.2. Mocninné funkce

Mocninná funkce je funkce ve tvaru

\[y=x^k, \]

kde \(x\) je proměnná (základ mocniny) a \(k\) číselný parametr (exponent). Exponent nemusí být celé číslo.

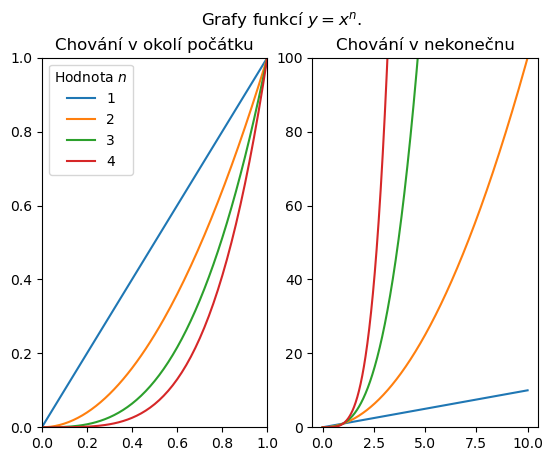
Chování mocninných funkcí je určeno exponentem. Pro kladné exponenty vyšší exponent znamená rychlejší růst pro velké hodnoty argumentu a rychlejší pokles k nule v okolí počátku.

Nakreslíme grafy mocninných funkcí. Pro názornost je vykreslíme dvakrát vedle sebe a jednou omezíme grafy na okolí počátku. Níže si můžete rozkliknout skript pto výpočet funkčních hodnot a vykreslení obrázku.

Show code cell source Hide code cell source

N = 1000
x = np.linspace(0,10,N)
mocniny = np.array([1,2,3,4])

x_sloupec = x.reshape((-1,1))
data = x_sloupec**mocniny
df = pd.DataFrame(data, index=x, columns=mocniny)

# Vykreslení dat z tabulky, dva grafy vedle sebe
fig,ax = plt.subplots(1,2)  # grafy do jednoho řádku a dvou sloupců
df.plot(ax=ax[0])     # levý graf
df.plot(ax=ax[1],legend=False) # pravý graf

# Popisky a rozsahy os nalevo
ax[0].legend(title=r"Hodnota $n$")
ax[0].set(
    xlim=(0,1), 
    ylim=(0,1), 
    title="Chování v okolí počátku")
# Popisky a rozsahy os napravo
ax[1].set(
    ylim=(0,100), 
    title="Chování v nekonečnu")
# Společný nadpis  
fig.suptitle(r"Grafy funkcí $y=x^n$.");

1.3.3. Polynomy

Polynom je součet násobků mocninných funkcí s celočíselným exponentem. Stupněm polynomu rozumíme hodnotu největšího exponentu. Například

\[ f(x)=x^3-2x^2+1\]

je polynom třetího stupně. Polynomy druhého stupně se nazývají kvadratické funkce, polynomy třetího stupně se nazývají kubické funkce.

Chování polynomu v nekonečnu určuje člen s nejvyšší mocninou. Například polynom

\[y=-2x^4+3x^3+5x+2 \]

je pro velká \(x\) záporný, stejně jako funkce \(y=-2x^4\). Pro \(x\) jdoucí k nekonečnu jdou funkční hodnoty do mínus nekonečna.

1.3.3.1. Kvadratické funkce

Kvadratickou funkcí rozumíme funkci ve tvaru polynumu druhého stupně

\[ y=ax^2+bx+c, \]

kde \(a\neq 0\). Je-li výraz \(b^2-4ac\) kladný, má polynom dva reálné kořeny

\[ x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}. \]

a platí

\[ y=a(x-x_1)(x-x_2)., \]

Grafem kvadratické funkce je parabola s průsečíky na ose v bodech \(x=x_1\) a \(x=x_2\). Pro \(a>0\) je otočená vrcholem dolů, v opačném případě vrcholem nahoru.

Vrchol paraboly, která má dva reálné kořeny, má \(x\)-ovou souřadnici uprostřed mezi kořeny, tj.

\[ x_{\text{vrchol}}=\frac{x_1+x_2}{2}=-\frac{b}{2a}. \]

Vzorec

\[ x_{\text{vrchol}}=-\frac{b}{2a}. \]

platí i když parabola nemá reálné nulové body a je celá nad vodorovnou nebo pod vodorovnou osou.

1.3.3.1.1. Logistický růst

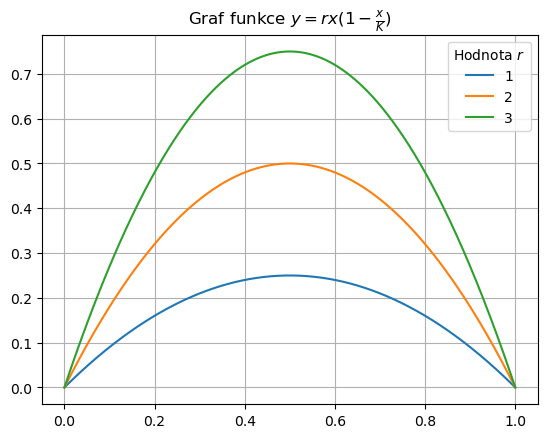
Kvadratická funkce se v modelech populací vyskytuje často v modelech zohledňujících vnitrodruhovou konkurenci. V takovém případě zpravidla předpokládáme, že rychlost růstu populace je úměrná velikosti populace a volnému místu v prostředí s konečnou nosnou kapacitou. Toto volné místo zpravidla vyjadřujeme procentem obsazenosti prostředí. Jednoduchým matematickým modelem rychlosti takového růstu je funkce

\[ f(x)=rx\left(1-\frac xK\right), \]

kde \(K\) je nosná kapacita prostředí a \(r\) je invazní parametr (specifická rychlost růstu pro malé velikosti populace). Tato kvadratická funkce proměnné \(x\) s parametry \(r\) a \(K\) má graf parabolu otočenou vrcholem nahoru s nulovými body \(x=0\) a \(x=K\).

Pro rostoucí \(r\) a pevné \(K\) se nemění poloha nulových bodů funkce, ale rostou její funkční hodnoty.

Show code cell source Hide code cell source

K = 1
x = np.linspace(0,1,1000)  # interval a počet bodů použitých pro kreslení         
df = pd.DataFrame(index=x) # nova tabulka
seznam_r = [1,2,3]
# dopocitani funkcnich hodnot
# pro ruzne nastaveni r
# jde udelat i bez pouziti cyklu, ale o tom jindy
for r in seznam_r:
    df[r] = r*x*(1-x/K)
df  # tisk tabulky pro kontrolu

	1	2	3
0.000000	0.000000	0.000000	0.000000
0.001001	0.001000	0.002000	0.003000
0.002002	0.001998	0.003996	0.005994
0.003003	0.002994	0.005988	0.008982
0.004004	0.003988	0.007976	0.011964
...	...	...	...
0.995996	0.003988	0.007976	0.011964
0.996997	0.002994	0.005988	0.008982
0.997998	0.001998	0.003996	0.005994
0.998999	0.001000	0.002000	0.003000
1.000000	0.000000	0.000000	0.000000

1000 rows × 3 columns

Show code cell source Hide code cell source

ax = df.plot() # vykresleni dat z tabulky
ax.grid() # vylepseni obrazku
ax.set(title=r"Graf funkce $y=rx(1-\frac {x}{K})$")
ax.legend(title=r"Hodnota $r$");

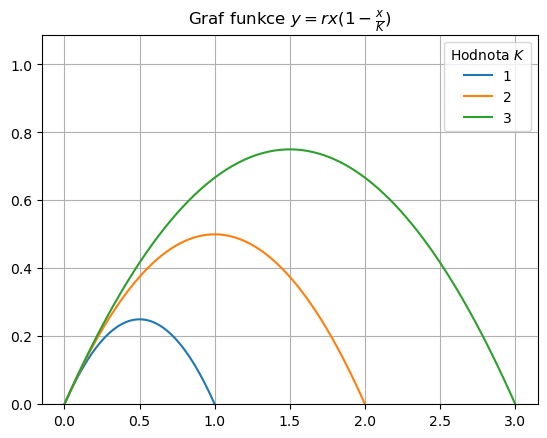
Pro rostoucí \(K\) a pevné \(r\) se nemění směr růstu paraboly v okolí počátku, ale roste se kladný kořen a rostou i funkční hodnoty.

Show code cell source Hide code cell source

r = 1
x = np.linspace(0,3,1000)  # interval a počet bodů použitých pro kreslení         
df = pd.DataFrame(index=x) # nova tabulka
# dopocitani funkcnich hodnot
# pro ruzne nastaveni K
for K in [1,2,3]:
    df[K] = r*x*(1-x/K)
    
ax = df.plot() # vykresleni dat z tabulky
ax.grid() # vylepseni obrazku
ax.set(title=r"Graf funkce $y=rx(1-\frac {x}{K})$")
ax.legend(title=r"Hodnota $K$")
ax.set(ylim=(0,None));

1.3.4. Racionální funkce

Racionální funkce jsou podílem dvou polynomů.

• Pokud je stupeň polynomu v čitateli menší než stupeň polynomu ve jmenovateli, funkce se v nekonečnu blíží k nule.

• Pokud mají čitatel i jmenovatel stejný stupeň, funkce má v nekonečnu vodorovnou asymptotu různou od nuly.

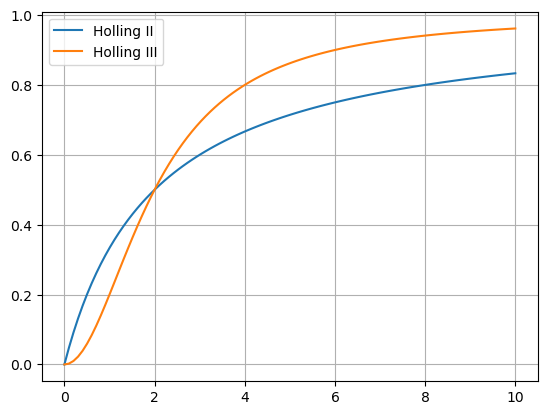
V ekologii se často používají funkce, modelující specifickou funckionální odezvu. Setkáme se s nimi pozěji v modelech dravce a kořisti [7], [3]. Významnými funkcemi jsou takzvané funkce Hollingova typu, z nichž zmíníme typ Holling II a Holling III. V obou případech se jedná o kladné rostoucí funkce vycházející z počátku souřadné soustavy a konvergující k vodorovné asymptotě, přičemž Holling II vychází z počátku souřadnic pod ostrým úhlem a Holling III s vodorovnou tečnou a má tedy pomalejší náběh. Matematickými modely ve formě racionálních funkcí pro odezvu tohoto typu mohou být funkce

\[f(x)=\frac{x}{x+a}\]

pro Holling II a

\[f(x)=\frac{x^k}{x^k+a^k}, \quad k>1\]

pro Holling III. (V případě vzorce pro typ Holling III číslo \(k\) nemusí být celé a formálně se tedy nebude jednat o podíl dvou polynomů.)

Show code cell source Hide code cell source

x = np.linspace(0,10,100)
a = 2
df = pd.DataFrame(index=x)

df["Holling II"] = x/(x+a)
df["Holling III"] = x**2/(x**2+a**2)

df.plot()
plt.grid();

1.3.5. Exponenciální funkce a logaritmus

Exponenciální funkce je mocnina s pevným základem a proměnným exponentem. Exponenciální funkce je prostá a její inverze je logaritmická funkce. V modelech nejčastěji pracujeme s přirozenými logaritmy a exponenciální funkcí o základu \(e\). Vzhledem k rovnosti

\[ a^x = e^{x\ln a}\]

základ exponenciální funkce není podstatný a libovolnou exponenciální funkci je možné přepsat na exponenciální funkci o libovolném základě.

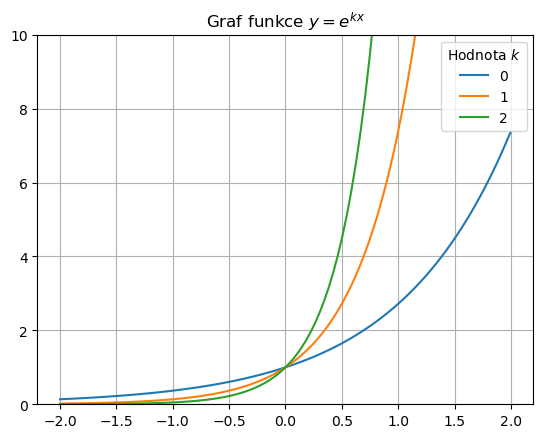
Funkce \(y=e^{kx}\) pro \(k\) kladné je rostoucí v nekonečnu (roste rychleji než polynom libovolného stupně) a klesající v mínus nekonečnu (klesá k nule rychleji než libovolná racionální funkce). Hodnota \(k\) reguluje rychlost růstu do nekonečna a poklesu k vodorovné asymptotě.

Show code cell source Hide code cell source

x = np.linspace(-2,2,100)
seznam_k = [1,2,3]

k = np.array(seznam_k).reshape((-1,1))  # hodnoty parameru do sloupce
data = np.exp(k*x) # vypocet vsech hodnot
df = pd.DataFrame(data.T, index=x)  # sestaveni tabulky, data z radku do sloupcu

ax = df.plot()
ax.set(ylim = (0,10),
       title = r"Graf funkce $y=e^{kx}$")
plt.legend(title=r"Hodnota $k$")       
plt.grid();

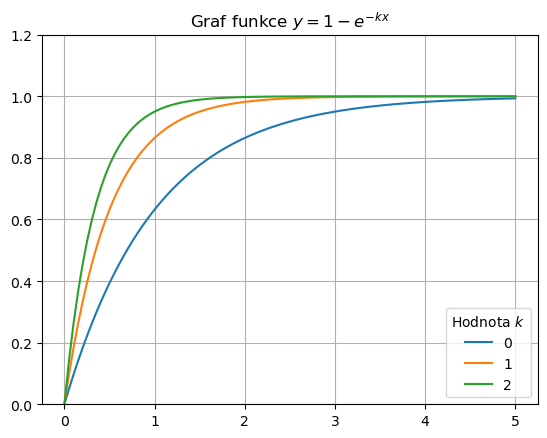
Funkce \(y=a+e^{-kx}\) (kde \(k\) je kladné) klesá shora k vodorovné asymptotě \(y=a\) tím rychleji, čím je vyšší hodnota \(k\). Funkce \(y=a-e^{-kx}\) se chová analogicky, ale k asymptotě roste.

Show code cell source Hide code cell source

x = np.linspace(0,5,100)
seznam_k = [1,2,3]

k = np.array(seznam_k).reshape((-1,1))  # hodnoty parameru do sloupce
data = 1 - np.exp(-k*x) # vypocet vsech hodnot
df = pd.DataFrame(data.T, index=x)  # sestaveni tabulky, data z radku do sloupcu

ax = df.plot()
ax.set(ylim = (0,1.2),
       title = r"Graf funkce $y=1-e^{-kx}$")
plt.legend(title=r"Hodnota $k$")       
plt.grid();

Pomocí exponenciálních funkcí je možno modelovat funkce Hollingova typu II a III například vztahy

\[y=1-e^{-kx}\]

pro typ Holling II a

\[y=1-e^{-kx^2}\]

pro typ Holling III.

Show code cell source Hide code cell source

x = np.linspace(0,4,100)
df = pd.DataFrame(index=x)
df["Holling II"] = 1-np.exp(-x)
df["Holling III"] = 1-np.exp(-x**2)

df.plot()
plt.grid();

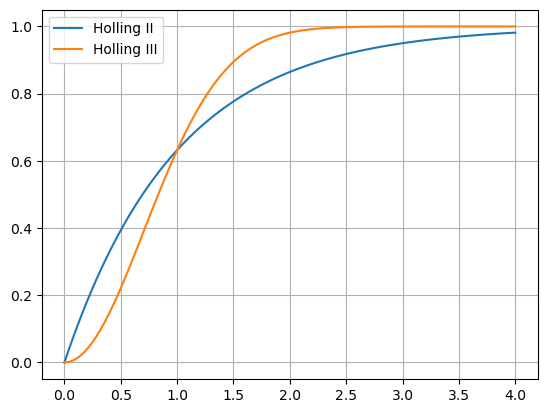
Tyto funkce mají podobný tvar jako analogické funkce uvedené v kapitole o racionálních funkcích, ale charakter závislosti je poněkud jiný a na základě empirických dat se zpravidla rozhodujeme, který způsob popisu nejlépe vyhovuje zkoumané realitě.

Exponenciální funkce s kladným koeficientem v exponentu modeluje růst, kdy rychlost růstu veličiny je úměrná velikosti této veličiny, tj. s tím jak veličina roste se zrychluje i rychlost jejího růstu. Exponenciální funkce se záporným koeficientem v exponentu se vyskytuje často tam kde systém konverguje do stacionárního stavu. Potom často vzdálenost od stacionárního stavu exponenciálně klesá s časem.

1.3.6. Složené funkce

Často je nutné modifikovat chování funkce podle aktuální potřeby. Například zařídit, aby funkce nerostla k jedničce, ale k jiné hodnotě. Někdy potřebných požadavků můžeme dosáhnout tak, že namísto s funkcí pracujeme s jejím násobkem, nebo do ní namísto proměnné dosazujeme násobek proměnné. Tedy namísto s funkcí \(y=f(x)\) pracujeme s funkcí \(y=k_1f(k_2x)\), jejíž graf dostaneme z grafu funkce \(y=f(x)\) natažením \(k_1\)-krát ve svislém směru a zúžením \(k_2\)-krát ve vodorovném směru. Viz následující obrázek.

Show code cell source Hide code cell source

x = np.linspace(-3,3,100)
df = pd.DataFrame(index=x)
df["1"]=np.exp(-x**2)
df["2"]=np.exp(-(3*x)**2)
df["3"]=3*np.exp(-x**2)
df["4"]=3*np.exp(-(3*x)**2)
ax = df.plot(
    subplots=True, 
    layout=(2,2),
    sharex=True,
    sharey=True,
    legend=False,
    title="Efekt lineární transformace na graf",
    grid=True
    )
ax[0,0].set(title=r"$e^{-x^2}$")
ax[0,1].set(title=r"$e^{-(3x)^2}$")
ax[1,0].set(title=r"$3e^{-x^2}$")
ax[1,1].set(title=r"$3e^{-(3x)^2}$");

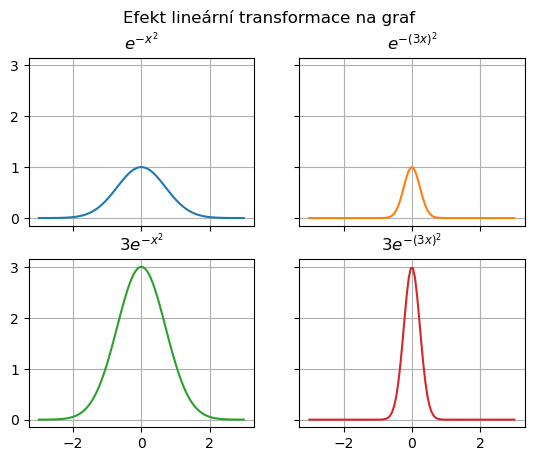
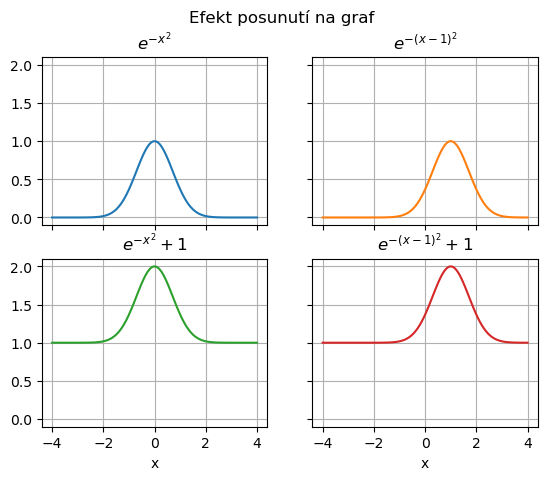
Podobně je možno sledovat vliv posunutí. Přičtení konstantní hodnoty k funkci značí posun grafu ve vertikálním směru, přičtení konstantní hodnoty k argumentu posun ve vodorovném směru. Přičtení kladné hodnoty způsobí posun grafu nahoru resp. doleva, přičtení záporné hodnoty posun na opačnou stranu.

Show code cell source Hide code cell source

x = np.linspace(-4,4,100)
df = pd.DataFrame()
df["x"]=x
df["1"]=np.exp(-x**2)
df["2"]=np.exp(-(x-1)**2)
df["3"]=np.exp(-x**2)+1
df["4"]=np.exp(-(x-1)**2)+1
ax = df.plot(
    x="x", 
    subplots=True, 
    layout=(2,2),
    sharex=True,
    sharey=True,
    legend=False,
    title="Efekt posunutí na graf",
    grid=True
    )
ax[0,0].set(title=r"$e^{-x^2}$")
ax[0,1].set(title=r"$e^{-(x-1)^2}$")
ax[1,0].set(title=r"$e^{-x^2}+1$")
ax[1,1].set(title=r"$e^{-(x-1)^2}+1$");

1.4. Funkce více proměnných a vektorové funkce

V praxi se neomezujeme na funkce, které mají na vstupu jedno číslo a vracejí jako funkční hodnotu opět jedno číslo, ale proměnných na vstupu i na výstupu může být více.

1.4.1. Skalární funkce více proměnných

Typickým případem kdy na vstupu funkce je více veličin a na výstupu veličina jediná je rychlost růstu populace, jejíž nosná kapacita je ovlivněna jinou populací. Jsou-li velikost populace \(x\) a velikost populace konkurenta \(y\), můžeme k modelování takové rychlosti růstu použít funkce

\[ f(x,y)=rx\left(1-\frac x{K+\alpha y} \right) \]

nebo

\[ f(x,y)=rx\left(1-\frac xK - \alpha y \right),\]

kde nám kromě invazního parametru \(r\) a nosné kapacity prostředí \(K\) přibyl parametr \(\alpha\) charakterizující sílu mezidruhové konkurence. Je-li \(f\) funkce dvou proměnných, píšeme \(f\colon \mathbb{ R^2}\to\mathbb{R}.\)

Vizualizace funkce dvou proměnných může být realizována jako plocha ve 3D prostoru, což však někdy nedává zcela názornou představu. Další možností je s druhou proměnnou zacházet jako s parametrem a kreslit graf funkce jedné proměnné pro vybrané pevné hodnoty druhé proměnné.

1.4.2. Vektorová funkce jedné proměnné

Vektorová funkce jedné proměnné je funkce, která má na vstupu jednu proměnnou a na výstupu více proměnných, které zpravidla uvažujeme jako komponenty vektoru. Typickým případem je časový průběh velikosti dvou populací.

Vizualizovat funkci můžeme tak, že nakreslíme graf každé komponenty samostatně (pokud kreslíme do jednoho obrázku, můžeme použít dvě osy \(y\)). Je-li výstupem vektor v rovině, můžeme funkci vizualizovat tak, že kreslíme uspořádané dvojice pro různé hodnoty vstupních dat.

Upozornění.

Představené datové řady je nutné brát jenom ilustrativně. Nejedná se o data se spolehlivou interpretací (namísto velikosti populací se pravděpodobně jedná o množství vykoupených kožešin), pravděpodobně byla získána z grafů v dřívějších publikacích a nejsou ani stejná napříč různými publikacemi.

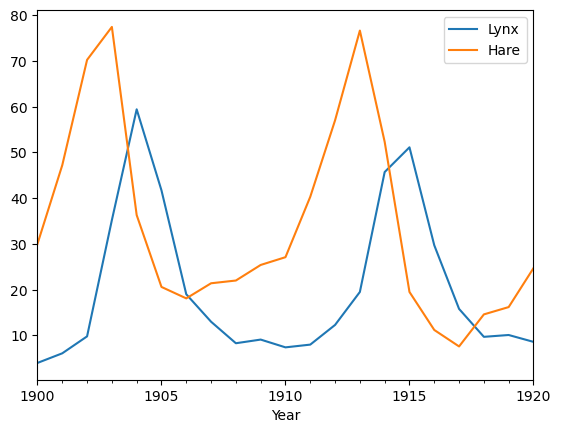
Na obrázku je vektorová funkce, kde vstupem je rok a výstupem je velikost populace zajíce běláka (angl. hare) a sněžného rysa (angl. lynx) v oblasti Hudsonova zálivu. V matematické biologii je to jeden z nejznámějších modelů vzájemného působení populací. Data stáhneme ve formě csv souboru do tabulky a pro kontrolu vytiskneme začátek tabulky.

Show code cell source Hide code cell source

zdroj = "https://raw.githubusercontent.com/robert-marik/dmp/main/data/hudson_bay_lynx_hare.csv"
df = pd.read_csv(zdroj, skiprows=2)
df.Year = pd.to_datetime(df.Year, format='%Y')
df.head()

	Year	Lynx	Hare
0	1900-01-01	4.0	30.0
1	1901-01-01	6.1	47.2
2	1902-01-01	9.8	70.2
3	1903-01-01	35.2	77.4
4	1904-01-01	59.4	36.3

Vykreslení dat pro jednotlivé druhy je snadné, stačí zadat, jaká veličina má být na vodorovné ose.

Show code cell source Hide code cell source

df.plot(x="Year");

Znázornění v rovině zajíc–rys je také snadné, zadáme veličiny pro vodorovnou a svislou osu a malinko graf vylepšíme přidáním teček, letopočtů a popisku.

Show code cell source Hide code cell source

ax = df.plot(x="Hare",y="Lynx", ylabel="Lynx", style="o-", legend=False)
for i,row in df.iterrows():
    ax.text(row['Hare'],row['Lynx'],row['Year'].year)

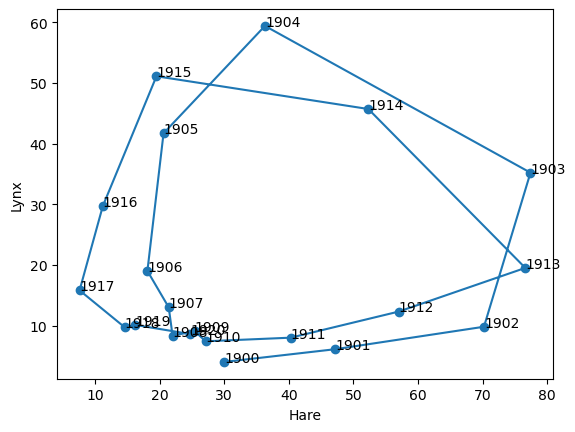
V tomto případě v rovině zajíc–rys vektorová funkce představuje parametricky zadanou křivku, resp. pokud je funkce dána jenom hodnotami z tabulky, potom se křivka redukuje na lomenou čáru. Podobně je možno chápat libovolnou vektorovou funkci jedné proměnné jako parametrickou křivku v prostoru příslušné dimenze.

1.4.3. Vektorové pole

Vektorové pole je funkce, která má na vstupu vektor a na výstupu opět vektor, zpravidla stejné dimenze jako vektor na vstupu. Potom je obvyklé chápat vektor na vstupu jako bod a vektor na výstupu jako vektor s počátkem v uvedeném bodě. Při takovém chápání je poměrně účinné vizualizovat vektorové pole v rovině, tj. funkci, mající na vstupu i na výstupu dvě proměnné. Proměnné na vstupu chápeme jako body v rovině a proměnné na výstupu chápeme jako komponenty orientované úsečky s počátkem v uvažovaném bodě. (Odsud je i název vektorové pole, protože při vizualizaci obdržíme systém orientovaných úseček v rovině. Protože by zpravidla byl výsledný obrázek nepřehledný, délku vektorů můžeme v obrázku sjednotit a informaci o původní délce vyjádřit barevně.

Show code cell source Hide code cell source

# Body pro kresleni
x, y = np.meshgrid(np.linspace(-5, 5, 10), 
                   np.linspace(-5, 5, 10))

# Komponenty vektoroveho pole
u = -y/(1 + x**2 + y**2)
v = x/(1 + x**2 + y**2)

M = np.sqrt(u**2+v**2) # velikost vektoru
qq=plt.quiver(x,y,u/M,v/M,M,cmap=plt.cm.jet, angles="xy") # vykresleni s jednotkovou delkou
plt.colorbar(qq) # barevna skala pro delku vektoru
plt.gca().set_aspect(1) # stejne meritko na obou osach
plt.show();

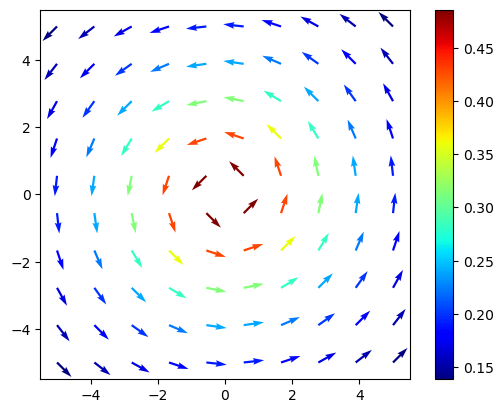
Někdy může být ilustrativnější chápat vektorové pole jako rychlostní pole a vykreslit si příslušný tok.

Show code cell source Hide code cell source

plt.streamplot(x,y,u,v) # vykresleni toku
plt.gca().set_aspect(1) # stejne meritko na obou osach
plt.show();

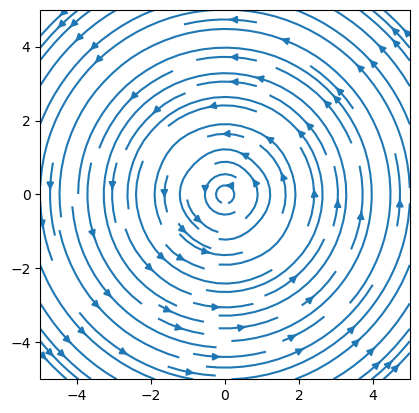
Tento způsob vizualizace budeme používat při modelování vývoje dvoudruhových populací, například při modelování konkurence nebo vztahu dravce a kořisti. Vektorové pole bude udávat trend, jakým směrem se bude systém vyvíjet a řešením budou parametrické křivky, podobné výše uvedenému příkladu s rysem a zajícem.