Ctrl+K

Modely konkurence populací

10. Modely konkurence populací#

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

10.1. Lotkův–Volterrův model konkurence dvou populací#

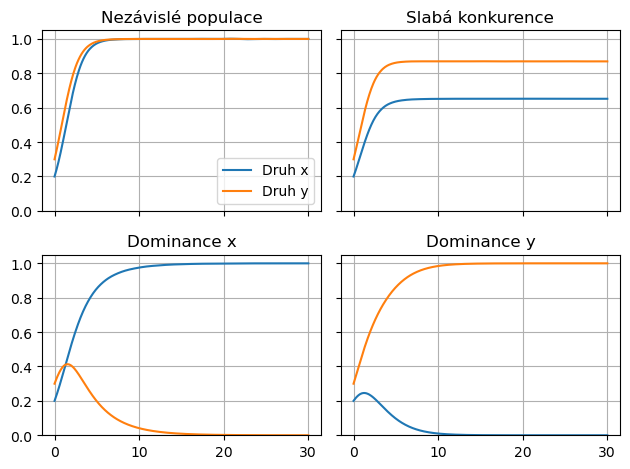
Namodelujte jednotlivé situace ve společenství dvou kořistí. Využijte tabulky s hierarchickými jmény sloupců podle ukázky. Kód je přepsán níže.

  • Prostudujte kód a poté vyplňte následující úkoly. (Ukázky, co by mělo být výstupem a některé rady najdete níže.)

  • Úkol 1 spočívá v nahrazení případu neovlivňujících se populací případem silné konkurence dvou populací. Změna bude na dvou místech: nadpis grafu a parametry mezidruhové konkurence.

  • Úkol 2 spočívá v demonstraci toho, že silná konkurence se odlišuje od ostatních v tom, že různé počáteční hustoty soupeřících populací moou vést ke konkurečnímu vyloučení různých populací. Nejlépe to ukážete tak, že najdete dvě řešení stejného systému, ale s různými počátečními podmínkami tak, aby u silné konkurence jednou byla vyloučena jedna a podruhé druhá populace.

def konkurence(t,X,a=1,b=1,c=0.4,alpha=1,beta=.2,gamma=1):
    x,y = X
    return [(a-b*x-c*y)*x, (alpha-beta*x-gamma*y)*y]

meze = [0,30]
pocatecni_podminka = [0.2,0.3]
t = np.linspace(*meze,500)

my_index = pd.MultiIndex.from_tuples([], names=['dataset', 'populace'])
df = pd.DataFrame(columns=my_index, index=t)
datasets = ["nezávislé populace","slabá konkurence","dominance x","dominance y"]  # Názvy datasetů
druhy = ["x","y"] # Názvy druhů

for c,beta,d in zip( 
                [0,0.4,0.4,1.5],   # hodnoty pro koeficient c 
                [0,0.2,1.3,0.8],   # hodnoty pro koeficient beta
                datasets  # názvy datasetů
        ):
    reseni = solve_ivp(
                       lambda t,X:konkurence(t,X,c=c,beta=beta),
                       meze,
                       pocatecni_podminka,
                       t_eval=t 
                       ).y.T   # řešení ve sloupcích
    df[[(d,druh) for druh in druhy]]=reseni # uložení do tabulky
df.tail() # tisk konce tabulky pro kontrolu
dataset nezávislé populace slabá konkurence dominance x dominance y
populace x y x y x y x y
29.759519 0.999867 0.999926 0.652025 0.869367 0.999876 0.000107 6.607543e-07 0.999999
29.819639 0.999875 0.999931 0.652022 0.869363 0.999880 0.000105 6.411905e-07 0.999999
29.879760 0.999882 0.999935 0.652022 0.869363 0.999885 0.000103 6.222057e-07 0.999999
29.939880 0.999889 0.999938 0.652026 0.869368 0.999889 0.000101 6.037822e-07 0.999999
30.000000 0.999895 0.999942 0.652032 0.869376 0.999893 0.000099 5.859032e-07 0.999999 
fig,axs = plt.subplots(2,2,sharex=True, sharey=True)  # obrázek se čtyřmi podobrázky ve dou řadách a sloupcích
axs = axs.ravel()  # abychom se nemuseli na podobrázky odkazovat dvojitým indexem, seřadíme je lineárně
for ax,dataset in zip(axs,datasets):  # cyklus přes podobrázky a datasety
    ax.plot(df.xs(key=(dataset,"x"),level=(0,1),axis=1))  # vykreslení datasetu do podobrázku, populace x
    ax.plot(df.xs(key=(dataset,"y"),level=(0,1),axis=1))  # vykreslení datasetu do podobrázku, populace y
    ax.set(  # nastavení nadpisu
        title=dataset.capitalize()
        )
    ax.grid()
axs[0].set(ylim=(0,1.05))    # rozsah pro svislou osu
axs[0].legend([f"Druh {i}" for i in druhy])  # legenda
plt.tight_layout()  # automatické upravení mezer mezi obrázky
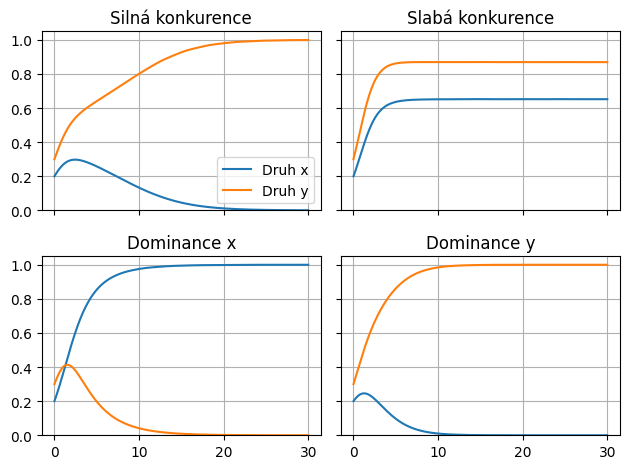
../_images/ba2064b69451e064df6c5506c20fe07eb92d42e3b0260259b506de820a1fc48a.png

10.1.1. K Úkolu 1.#

Změňte první scénář (nezávislé populace) na silnou konkurenci. Měli byste dostat něco jako následující obrázek.

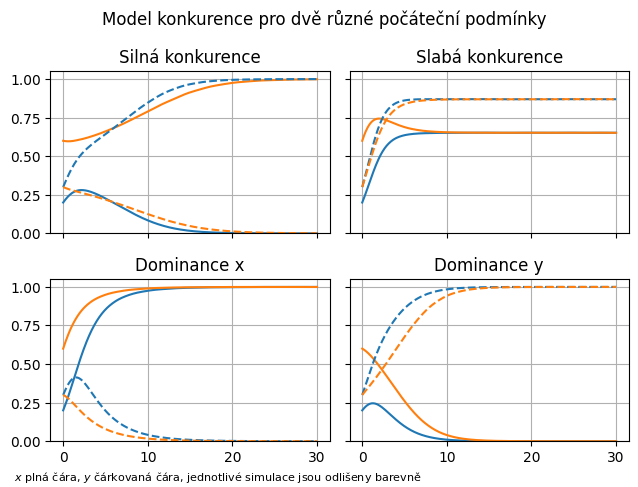
10.1.2. K Úkolu 2.#

Rozšiřte kód tak, aby dokázal zpracovat dvě počáteční podmínky. Ukažte, že pro jiné počáteční podmínky ve třech případech konverguje systém do stejného stavu, ale u silné konkurence může dojít k vymření populace, která při jiných počátečních podmínkách dominuje. Kreslete každou populaci jiným druhem čáry a stejné simulace (ze stejné počáteční podmínky) stejnou barvou. Měli byste dostat něco jako následující obrázek.

  • Rozšíření udělejte v cyklu tak, aby se dal simulovat libovolný počet počátečních podmínek. Budete tedy muset udělat následující.

    • Počáteční podmínky je vhodné umístit do jednoho seznamu, například pocatecni_podminky = [[0.2,0.3],[0.6,0.3]].

    • Je nutné rozšířit nadpis sloupců o další úroveň zachycující počáteční podmínku. Předřaďte například jako úroveň pojmenovanou pocatecni podminka jako první. Příkazy pro ukládání do tabulky a pro kreslení je potom nutno upravit tak, aby pracovaly se správnými daty (přibyla jedna úroveň sloupcového indexu), aby se kreslilo potřebnou čarou a správnými barvami.

    • Cyklus

      for c,beta,d in ... 
    reseni = ...
    df[[(d,druh) for druh in druhy]]=reseni

      je nutné zaměnit za něco jako

      for c,beta,d in ... 
    for i,pocatecni_podminka in enumerate(pocatecni_podminky):
        reseni = ...
        df[[(i,d,druh) for druh in druhy]]=reseni

      Tím se bude tvořit tabulka, která má simulace pro více počátečních podmínek odlišených v první úrovni nadpisu sloupců.

  • Pro nadpis nad obrázkem použijte například plt.suptitle("Nadpis ...")

  • Pro komentář pod třetí souřadnou soustavou (vlevo dole) použijte například plt.annotate("$x$ plná čára, $y$ čárkovaná čára, jednotlivé simulace jsou odlišeny barevně",xy=(10,5),xycoords='figure points',fontsize=8);. Vložte až pod příkaz tight_layout.

  • Čárkované čáry se dají udělat pomocí linestyle nebo zkráceně ls. Například

    x = np.linspace(0,10)
plt.plot(x,x**2,ls="--")

  • Přerušení cyklování barev a návrat na začátek cyklu se dá zařídit například následovně pomocí set_prop_cycle.

    x = np.linspace(0,1)
fig,ax = plt.subplots()
ax.plot(x,x**2) # první barva
ax.plot(x,x**2-0.2) # druhá barva
ax.plot(x,x**2+0.2) # třetí barva
ax.set_prop_cycle(None)           # reset cyklovače barev
ax.plot(x,x) # opět první barva
ax.plot(x,x-0.1) # opět druhá barva

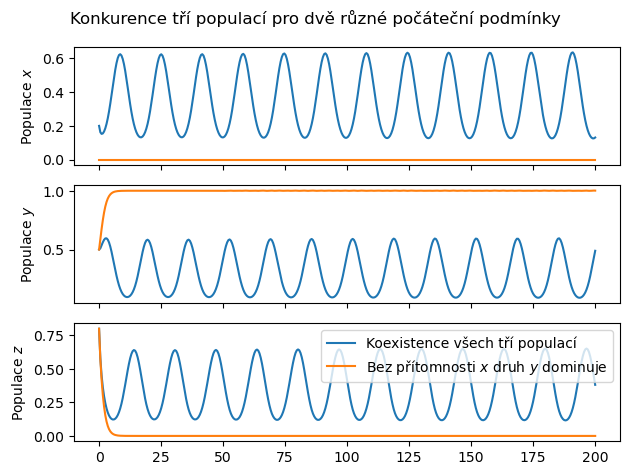
10.2. Konkurence tří populací#

meze = [0,200]
def konkurence_tri(t,X,
                   a=1,b=1,c=0.4,d=0.4,
                   alpha=1,beta=0.5,gamma=1,delta=0.5,
                   m=1,n=0.7,o=0.2,p=1
                   ):
    x,y,z = X # Rozbalení vektoru na tři populace
    return [
        (a-b*x-c*y-d*z)*x, # Vývoj populace x
        (alpha-beta*x-gamma*y-delta*z)*y, # Vývoj populace y
        (m-n*x-o*y-p*z)*z # Vývoj populace z
        ]

# Hodnoty parametrů a,b,c,d,...
parametry = (1, 1,   0.3, 1.6,
             1, 1.8, 1,   0.2,
             1, 0.3, 1.8, 1  )

pocatecni_podminky = [ [.2,.5,0.8],
                       [0,.5,0.8],
                     ]
populace = ["x","y","z"]
idx = pd.MultiIndex.from_tuples([],names=["pocatecni_podminka","populace"])
t = np.linspace(*meze,400)
df = pd.DataFrame(columns=idx, index=t)

for i,pocatecni_podminka in enumerate(pocatecni_podminky):
    reseni = solve_ivp(
        lambda t,X: konkurence_tri(t,X,*parametry),
        meze,
        pocatecni_podminka,
        t_eval=t,
        ).y.T
    df[[(i,p) for p in populace]] = reseni
df
pocatecni_podminka 0 1
populace x y z x y z
0.000000 0.200000 0.500000 0.800000 0.0 0.500000 8.000000e-01
0.501253 0.162531 0.510449 0.581288 0.0 0.587140 5.747068e-01
1.002506 0.152474 0.535269 0.453523 0.0 0.672641 4.221983e-01
1.503759 0.155041 0.561444 0.364051 0.0 0.749448 3.058208e-01
2.005013 0.166445 0.582453 0.296722 0.0 0.814145 2.189325e-01
... ... ... ... ... ... ...
197.994987 0.139864 0.275323 0.592602 0.0 0.999302 1.446128e-30
198.496241 0.130372 0.326898 0.548750 0.0 0.999981 2.583605e-30
198.997494 0.125782 0.382066 0.496533 0.0 1.000916 5.053235e-30
199.498747 0.125932 0.437562 0.439419 0.0 1.001337 6.104828e-30
200.000000 0.130852 0.489458 0.381156 0.0 1.000848 4.222711e-30

400 rows × 6 columns

fig,ax = plt.subplots(len(populace),sharex=True) # Tři obrázky se sdílenou časovou osou
for a,kdo in zip(ax,populace): # Cyklus přes dvojice obrázek+populace
    a.plot(df.xs(level=1,key=kdo,axis=1))  # Grafy pro obě počáteční podmínky
    a.set(ylabel=f"Populace ${kdo}$") # Popisek na svislou osu

# Kosmetika: nadpis obrázku, text legendy v jednom z obrázků a mezerování mezi obrázky
plt.suptitle("Konkurence tří populací pro dvě různé počáteční podmínky")        
ax[-1].legend(
    ["Koexistence všech tří populací",
     "Bez přítomnosti $x$ druh $y$ dominuje"],loc="upper right")
plt.tight_layout()
../_images/7f870e06e09a37e32df09b7f128d001099982fef25670cdd741771b9c11cd316.png

10.2.1. Úkol#

  1. Zkuste v systému nasadit ještě silnější míru konkurence. Všechny koeficienty mezidruhové konkurence, které jsou větší než jedna, zkuste dále navyšovat a sledovat, jestli neuvidíte nějaké další zajímavé chování.

  2. Zkuste snížit koeficienty charakterizující mezidruhovou konkurenci tak, aby systém konvergoval ke stacionárnímu řešení. Poté zkuste jedné z populací podpořit růst a sledujte, jestli má systém odezvu, která odpovídá provedené modifikaci.

  3. Vyzkoušejte si ukázky selekce sloupců v tabulce s multiindexem. Zkuste pro systém s koeficienty nastavující oscilatorické chování zakreslit časový průběh všech populací do jednoho obrázku.

Obsah