4. Diferenciální rovnice 1#
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from scipy.integrate import solve_ivp
Ve cvičení začínáme částí A, řešení modelu dynamické rovnováhy druhů z přednášky.
Kdo je schopen postupovat podle textu a řešit úkoly samostatně, může pracovat dopředu a pokračovat částí B, kde jsou na modelu ochlazování kávy možnosti příkazu pro řešení diferenciálních rovnic.
Část C se vrací k modelu dynamické rovnováhy, ukazuje příklad, jak je možné nakreslit křivky řídící rychlosti kolonizace a vymírání a jak je možné prozkoumat chování modelu při různých počátečních podmínkách a různých hodnotách parametru. Zájemci by měli být schopni si tyto pasáže projít sami.
4.1. Část A: Řešení diferenciální rovnice (modifikace existujícího kódu)#
Pokud jste rychlejší, řešte samostatně a pokračujte samostatně k části B s
detailnějším popisem příkazu solve_ivp.
4.1.1. Řešení rovnice a vizualizace řešení.#
Následující kód vyřeší rovnici
4.1.1.1. Úkoly:#
Prohlédnout si kód, ujasnit si co dělá, spustit.
Vyzkoušejte si zadání více počátečních podmínek, například řádek
pocatecni_podminka = [0]vyměňte zapocatecni_podminka = [0,5,10,20]. Tím získáte řešení pro několik počátečních podmínek současně.Vyzkoušejte si změnit úlohu. Vykopírujte text do nové buňky (můžete duplikovat buňku a kopii potom upravovat) a opravte tak, aby zobrazoval řešení počáteční úlohy
\[\frac{\mathrm dT}{\mathrm dt}=-0.1(T-20), \quad T(0)=100\]s ochlazováním kávy. I zde zkuste více počátečních podmínek.Vyzkoušejte si do půodního modelu ostrovní biodiverzity doplnit křivku odpovídající řešení pro ostrov ve dvojnásobné vzdálenosti od pevniny. Zkontrolujte, že kód kreslí dvě funkce a že se pro vzdálenější ostrov řešení chová tak, jak očekáváte. Pro začátek můžete recyklovat kód kde se řeší jedna rovnice a řetezit výpočty za sebe. Později si ukážeme lepší řešení. Pokud chcete všechny výstupy příkazu
plotmít v jednom obrázku, musíte je volat ve stejné buňce. Možná se bude hodit si nadefinovat funkcimodel2nějak takto.
def model2(t,N):
return model(t,N,D=1)
### Příprava funkcí a parametrů
pocatecni_podminka = [0] # počáteční podmínka nebo podmínky
meze = [0,15] # interval, na kterém hledáme řešení
n = 100 # počet dělících bodů
def model(t, N, a=1, b=8, beta=0.2, D=0.5, k=1.3, S=20):
"""
Funkce z pravé strany modelu dynamické rovnováhy počtu druhů na ostrovech,
podle McArthura a Wilsona.
Vstup:
-----
Povinnými parametry jsou čas a počet druhů, volitelnými vzdálenost
D od pevniny, rozloha ostrova S, další parametry modelu a konstanty
úměrnosti. Přednastavené hodnoty jsou pouze ilustrační, závisí na volbě
jednotek a konkrétním použití.
Výstup:
------
Hodnota funkce.
"""
kolonizace = b/(D*(N+beta))
vymirani = a*N**k/S
return kolonizace - vymirani
### Řešení modelu
t=np.linspace(*meze, n) # definiční obor, v těchto bodech budeme hledat řešení
reseni = solve_ivp(
model,
meze,
pocatecni_podminka,
t_eval=t
)
### Vizualizace řešení
fig,ax = plt.subplots(1)
ax.plot(t,reseni.y.T)
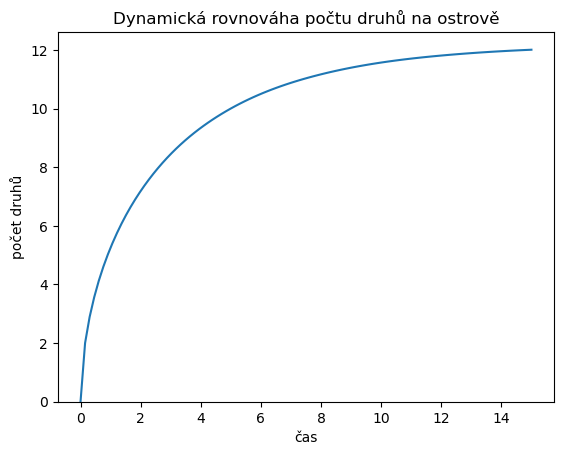
ax.set(
ylim = (0,None),
title = "Dynamická rovnováha počtu druhů na ostrově",
xlabel="čas",
ylabel="počet druhů",
);
?model
4.1.2. Řešení pro sadu parametrů#
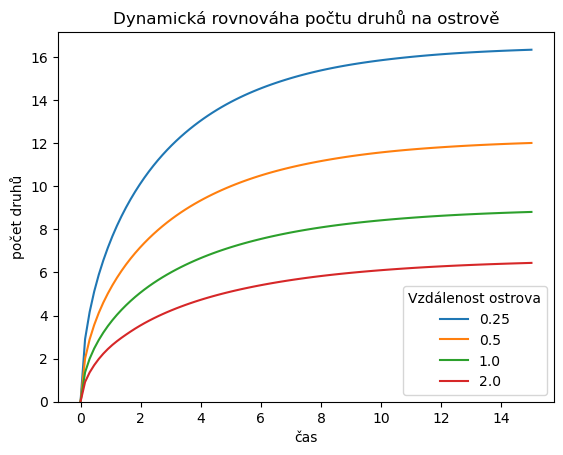
Následující kód řeší vícekrát rovnici dynamické rovnováhy pro několik různých vzdálenosti ostrova od pevniny optimálním způsobem, kdy parametry získáme z předdefinovaného seznamu, nejprve vypočteme všechna řešení a data uložíme do tabulky a teprve poté data vykreslíme. Tím je jasně daná struktura, kde se připravují výpočty, kde se počítají data a kde se data prezentují. Pro malé projekty toto není tak důležité, při delším kódu to značně zvýsí přehlednost s udržovatelnost.
V čem se kód změní od předchozího? Prohlédněgte si diff obou kódů.
Používá se proměnná se seznamem parametrů.
Data se ukládají do tabulky, protože místo jednoho řešení budeme mít řešení několik.
Ve volání příkazu
solve_ivpse předává hodnota parametru.Příkazy pro řešení rovnice a uložení do tabulky jsou volány v cyklu.
Pro kreslení se dá použít metoda
plotpro tabulky.
### Příprava funkcí a parametrů
pocatecni_podminka = [0] # počáteční podmínka
meze = [0,15] # interval, na kterém hledáme řešení
n = 100 # počet dělících bodů
parametry = [0.25,0.5,1,2] # seznam parametrů
def model(t, N, a=1, b=8, beta=0.2, D=0.5, k=1.3, S=20):
"""
Funkce z pravé strany modelu dynamické rovnováhy počtu druhů na ostrovech,
podle McArthura a Wilsona.
Vstup:
-----
Povinnými parametry jsou čas a počet druhů, volitelnými vzdálenost
D od pevniny, rozloha ostrova S, další parametry modelu a konstanty
úměrnosti. Přednastavené hodnoty jsou pouze ilustrační, závisí na volbě
jednotek a konkrétním použití.
Výstup:
------
Hodnota funkce.
"""
kolonizace = b/(D*(N+beta))
vymirani = a*N**k/S
return kolonizace - vymirani
### Řešení modelu
t=np.linspace(*meze, n) # definiční obor, v těchto bodech budeme hledat řešení
df = pd.DataFrame(index=t, columns=parametry) # tabulka pro výstup
for parametr in parametry:
reseni = solve_ivp(
lambda t,x:model(t,x,D=parametr),
meze,
pocatecni_podminka,
t_eval=t
)
df[parametr] = reseni.y.T # další sloupec tabulky
# lambda funkce viz https://www.w3schools.com/python/python_lambda.asp
# (dočasná nepojmenovaná funkce)
### Vizualizace řešení
ax = df.plot()
ax.set(
ylim = (0,None),
title = "Dynamická rovnováha počtu druhů na ostrově",
xlabel="čas",
ylabel="počet druhů",
)
plt.legend(title="Vzdálenost ostrova");
4.1.2.1. Úkoly#
Vyzkoušejte si kód.
V nové buňce sledujte vliv rozlohy ostrova (vzdálenost je stejná) na druhovu skladbu. Vykopírujte si kód a proveďte příslušnou modifikaci.
Před každou buňku s výpočty vložte textovou buňku popisující, co se ve výpočtu odehrává, co se snažíme ukázat. Musíte vložit buňku, změnit typ z Code na Markdown (vybrat buňku a stisknout M, nebo použít rozbalovací menu v toolbaru a vepsat komentář.
Pokud jsou veličiny \(S\) a \(D\) ve stále stejném poměru, je stejná i hodnota, ke které konverguje řešení (viz přednáška).
Znamená to, že se budou populace vyvíjet stejně na daném ostrově a na ostrově, který je dvakrát větší a dvakrát dále? V čem se bude situace lišit a v čem bude stejná?
Odhadněte odpověď a potvrďte si hypotézu tak, že budete modelovat plnou diferenciální rovnici pro obě uvažované situace. Můžete použít něco jako
lambda t,x:model(t,x,D=0.5*nasobek,S=20*nasobek)a proměnnounasobeknechat iterovat přes seznam[1,2](případně delší seznam).
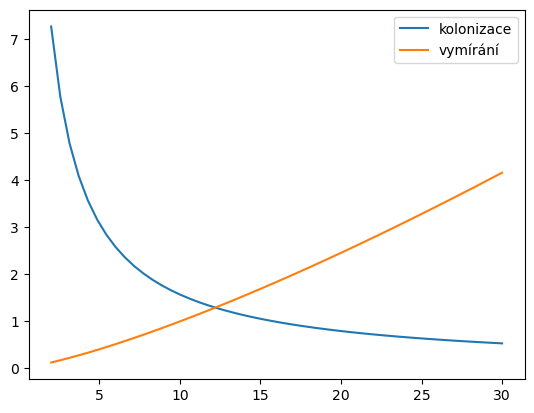
Vyzkoušejte si i následující kód (s nastavením funkce model jako v původní buňce). Vodorovně je velikost populace, svisle rychlost kolonizace resp. vymírání. Využíváme toho, že jeden z členů ve funkci z pravé strany rovnice lze eliminivat tak, že konstanta, která tento člen násobí, bude nulová.
def model(t, N, a=1, b=8, beta=0.2, D=0.5, k=1.3, S=20):
kolonizace = b/(D*(N+beta))
vymirani = a*N**k/S
return kolonizace - vymirani
N = np.linspace(2,30)
plt.plot(N,model(0,N,a=0),N,-model(0,N,b=0))
plt.legend(['kolonizace','vymírání'])
<matplotlib.legend.Legend at 0x7f720768b390>
4.2. Část B: Řešení diferenciální rovnice (podrobnější pohled pod kapotu)#
Příkaz solve_ivp dokáže vyřešit zadanou diferenciální rovnici pro několik počátečních podmínek. Použití je možné vidět na následujícím příkladě. Pro tři počáteční podmínky \(y(0)=2\), \(y(0)=4\) a \(y(0)=8\) řešíme rovnici
pocatecni_podminky = [2, 4, 8]
meze = [0,10]
def rovnice(t, y):
return -0.5 * y
sol = solve_ivp(rovnice, meze, pocatecni_podminky)
sol
message: The solver successfully reached the end of the integration interval.
success: True
status: 0
t: [ 0.000e+00 1.149e-01 1.264e+00 3.061e+00 4.816e+00
6.574e+00 8.333e+00 1.000e+01]
y: [[ 2.000e+00 1.888e+00 ... 3.107e-02 1.351e-02]
[ 4.000e+00 3.777e+00 ... 6.214e-02 2.702e-02]
[ 8.000e+00 7.553e+00 ... 1.243e-01 5.403e-02]]
sol: None
t_events: None
y_events: None
nfev: 44
njev: 0
nlu: 0
Následující příkazy vytisknou časy ve kterých bylo vypočteno řešení a hodnotu každého z řešení v daném čase.
print(sol.t)
print(sol.y)
[ 0. 0.11487653 1.26364188 3.06061781 4.81611105 6.57445806
8.33328988 10. ]
[[2. 1.88836035 1.06327177 0.43319312 0.18017253 0.07483045
0.03107158 0.01350781]
[4. 3.7767207 2.12654355 0.86638624 0.36034507 0.14966091
0.06214316 0.02701561]
[8. 7.5534414 4.25308709 1.73277247 0.72069014 0.29932181
0.12428631 0.05403123]]
Pro pohodnější práci je možné data zadat do tabulky, kde v prvním sloupci bude čas a v dalších sloupcích budou vypočtená řešení. Název sloupce bude dán počáteční podmínkou. Je vidět, že tímto číslem každé řešení i začíná.
df = pd.DataFrame()
df.index = sol.t
for i,j in zip(pocatecni_podminky, sol.y):
df[i] = j
df
| 2 | 4 | 8 | |
|---|---|---|---|
| 0.000000 | 2.000000 | 4.000000 | 8.000000 |
| 0.114877 | 1.888360 | 3.776721 | 7.553441 |
| 1.263642 | 1.063272 | 2.126544 | 4.253087 |
| 3.060618 | 0.433193 | 0.866386 | 1.732772 |
| 4.816111 | 0.180173 | 0.360345 | 0.720690 |
| 6.574458 | 0.074830 | 0.149661 | 0.299322 |
| 8.333290 | 0.031072 | 0.062143 | 0.124286 |
| 10.000000 | 0.013508 | 0.027016 | 0.054031 |
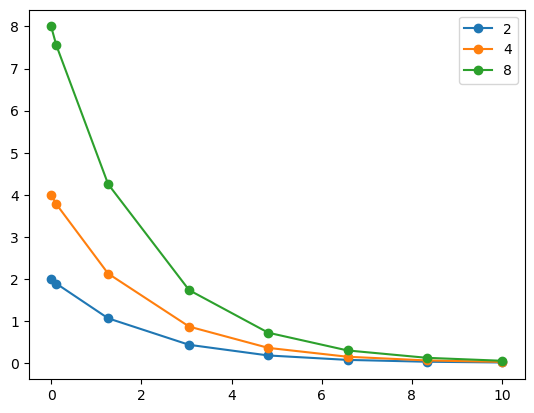
Po vykreslení vidíme, že graf je z lomených čar. Pro výraznost jsme přidali i tečky v bodech zlomu. To proto, že řešení byla vypočtena a v několika málo bodech.
df.plot(style="o-");
4.2.1. Úkol#
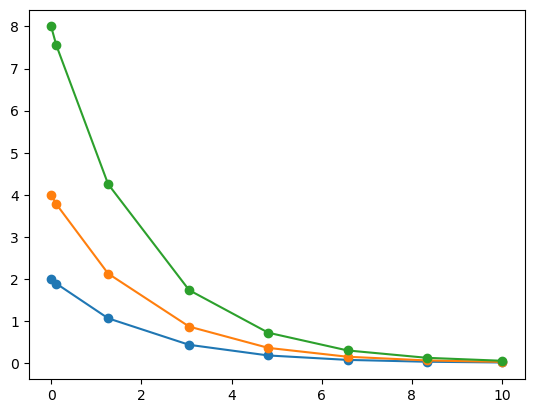
Vyzkoušejte si následující elegantnější příkazy. Pomocí nich nemusíme dělat cyklus přes jednotlivá řešení při sestavování tabulky a můžeme nakreslit všechna tři řešení jedním příkazem i bez sestavování tabulky. Snažte se zjistit, co dělá operátor T.
plt.plot(sol.t,sol.y.T,"o-");
df = pd.DataFrame(sol.y.T,columns=pocatecni_podminky)
df.index = sol.t
df
| 2 | 4 | 8 | |
|---|---|---|---|
| 0.000000 | 2.000000 | 4.000000 | 8.000000 |
| 0.114877 | 1.888360 | 3.776721 | 7.553441 |
| 1.263642 | 1.063272 | 2.126544 | 4.253087 |
| 3.060618 | 0.433193 | 0.866386 | 1.732772 |
| 4.816111 | 0.180173 | 0.360345 | 0.720690 |
| 6.574458 | 0.074830 | 0.149661 | 0.299322 |
| 8.333290 | 0.031072 | 0.062143 | 0.124286 |
| 10.000000 | 0.013508 | 0.027016 | 0.054031 |
pd.DataFrame(sol.y)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 2.0 | 1.888360 | 1.063272 | 0.433193 | 0.180173 | 0.074830 | 0.031072 | 0.013508 |
| 1 | 4.0 | 3.776721 | 2.126544 | 0.866386 | 0.360345 | 0.149661 | 0.062143 | 0.027016 |
| 2 | 8.0 | 7.553441 | 4.253087 | 1.732772 | 0.720690 | 0.299322 | 0.124286 | 0.054031 |
pd.DataFrame(sol.y.T)
| 0 | 1 | 2 | |
|---|---|---|---|
| 0 | 2.000000 | 4.000000 | 8.000000 |
| 1 | 1.888360 | 3.776721 | 7.553441 |
| 2 | 1.063272 | 2.126544 | 4.253087 |
| 3 | 0.433193 | 0.866386 | 1.732772 |
| 4 | 0.180173 | 0.360345 | 0.720690 |
| 5 | 0.074830 | 0.149661 | 0.299322 |
| 6 | 0.031072 | 0.062143 | 0.124286 |
| 7 | 0.013508 | 0.027016 | 0.054031 |
4.2.2. Řešení hladšími křivkami#
Řešení z minulých ukázek se skládalo z lomených čar. Nemělo spojitou derivaci, nebylo hladké. Pro hladší řešení je možné provést jednu nebo více z následujících vylepšení.
Zvolit menší krok, aby se vygenerovalo více hodnot pro čas \(t\),
Nastavit proměnnou
t_evalna dostatečně hustou posloupnost bodů. Toto jsme si vyzkoušeli v úvodní části.Nastavit hodnotu
dense_outputna True a řešení poté kreslit na husté množině bodů. Toto si vyzkoušíme níže.
Volba kroku také bývá základním testem korektnosti numerického řešení. Příliš velký krok může způsobit nepřesnosti v řešení, příliš malý krok je náročný na paměť i výpočetní výkon a také může vést k nepřesnostem. Obvyklým testem je porovnat řešení se zvoleným a s polovičním krokem. Pokud se shodují, je rozumné výsledek přijmout jako dobrou aproximaci přesného řešení.
sol = solve_ivp(
rovnice,
meze,
pocatecni_podminky,
dense_output=True,
# max_step=np.Inf, # defaultní nastavení je krok libovolné délky
)
sol
message: The solver successfully reached the end of the integration interval.
success: True
status: 0
t: [ 0.000e+00 1.149e-01 1.264e+00 3.061e+00 4.816e+00
6.574e+00 8.333e+00 1.000e+01]
y: [[ 2.000e+00 1.888e+00 ... 3.107e-02 1.351e-02]
[ 4.000e+00 3.777e+00 ... 6.214e-02 2.702e-02]
[ 8.000e+00 7.553e+00 ... 1.243e-01 5.403e-02]]
sol: <scipy.integrate._ivp.common.OdeSolution object at 0x7f720f9852b0>
t_events: None
y_events: None
nfev: 44
njev: 0
nlu: 0
t = np.linspace(*meze,500)
df = pd.DataFrame(np.array(sol.sol(t)).T,columns=pocatecni_podminky)
df.index = t
print(df.shape)
print(df.head())
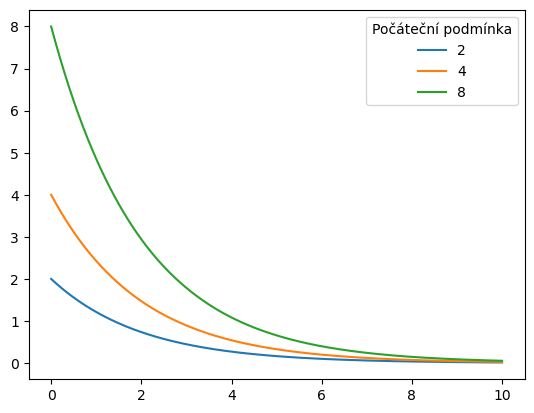
ax = df.plot()
ax.legend(title="Počáteční podmínka");
(500, 3)
2 4 8
0.00000 2.000000 4.000000 8.000000
0.02004 1.980060 3.960120 7.920240
0.04008 1.960319 3.920638 7.841275
0.06012 1.940774 3.881549 7.763098
0.08016 1.921425 3.842850 7.685699
4.2.3. Řešení rovnice pro různé hodnoty parametru#
Někdy potřebujeme řešit rovnici a sledovat, jak se chová řešení při změně parametru. Vyjdeme ze stejné počáteční podmínky a pro nastavené hodnoty parametru najdeme řešení.
def rovnice_r(t, y, r=1):
return -r*y # prava strana rovnice zavisi na parametru r
meze = [0,10]
hodnoty_r = [0.5,1,2,3]
pocatecni_podminka = [100] # Jedna pocatecni podminka
t = np.linspace(*meze,500) # hvezdicka rozbali pole na dve hodnoty pro dolni a horni mez
reseni = [solve_ivp(
rovnice_r,
meze,
pocatecni_podminka,
t_eval=t,
args=[r]
).y[0]
for r in hodnoty_r]
# vygenerovani reseni pro ruzne hodnoty parametru r |
df = pd.DataFrame(
np.array(reseni).T,
columns=hodnoty_r
)
df.index = t
print(df.shape) # tisk informaci o tabulce a graf
print(df.head())
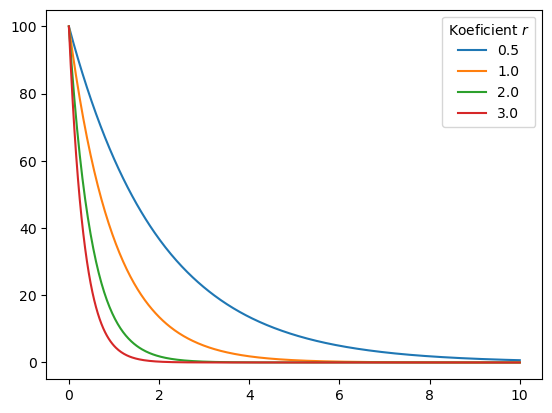
ax = df.plot()
ax.legend(title=r"Koeficient $r$");
(500, 4)
0.5 1.0 2.0 3.0
0.00000 100.000000 100.000000 100.000000 100.000000
0.02004 99.002999 98.015939 96.071240 94.165121
0.04008 98.015939 96.071242 92.296834 88.670711
0.06012 97.038719 94.165130 88.670717 83.496898
0.08016 96.071242 92.296836 85.186977 78.622903
Někdy se může hodit si funkci definující pravou stranu nepojmenovávat a nepředávat jí parametry. Například, pokud je její použití jednorázové. Potom je možno použít metodiku práce s nepojmenovanými funkcemi, takzvané lambda funkce. Ta umožňuje zadat pravou stranu rovnice přímo v příkazu solve_ivp.
hodnoty_r = [0.5,1,2,3]
pocatecni_podminka = [100] # Jedna pocatecni podminka
reseni = [solve_ivp(
lambda t,y: -r*y,
meze,
pocatecni_podminka,
t_eval=t
).y[0]
for r in hodnoty_r]
# vygenerovani reseni pro ruzne hodnoty parametru r
t = np.linspace(*meze,500) # hvezdicka rozbali pole na dve hodnoty pro dolni a horni mez
df = pd.DataFrame(np.array(reseni).T, columns=hodnoty_r, index=t)
ax = df.plot()
ax.legend(title=r"Koeficient $r$");

4.3. Část C: Model rovnováhy počtu druhů na ostrovech (volitelně, kdo je rychlejší a samostatný)#
V této části již nebude nic nového, ale je to ukázka, jak získané znalosti využít při studiu modelů.
Budeme studovat Mc Arthurův a Wilsonův model vývoje ostrovního společenství ve tvaru
První člen na pravé straně charakterizuje rychlost kolonizace, druhý člen rychlost vymírání.
Nakreslíme si křivky kolonizace a vymírání.
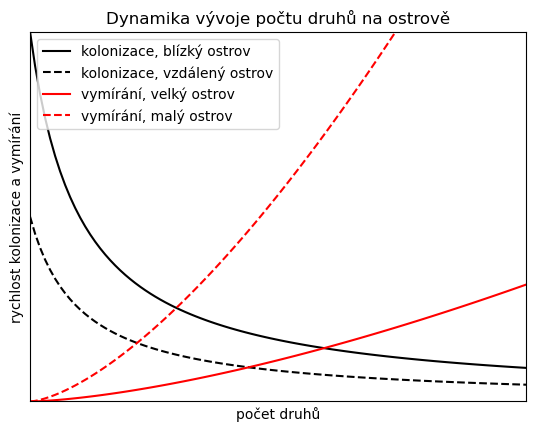
Nejprve překreslíme obrázek, který se často vyskytuje v publikacích k problematice. Dvě křivky vymírání pro dvě rozlohy ostrova, dvě křivky kolonizace pro dvě vzdálenosti ostrova od pevniny. Z jejich průsečíků je možné odhalit, při jakém počtu druhů nastane dynamická rovnováha.
V předchozím obrázku je příliš informací, což je někdy na škodu. Ve druhém obrázku necháme jenom jednu z křivek kolonizace, ať je lépe možné sledovat rovnovážnou polohu v závislosti na rozloze ostrova.
Dále vyřešíme model pro různé počáteční podmínky. Není překvapení, že vždy se nastolí rovnováha.
Nakonec vyřešíme model pro různé hodnoty parametru.
4.3.1. Grafy rychlostí kolonizace a vymírání#
Vykreslíme křivky kolonizace a vymírání (přesněji, rychlostíi těchto dějů) v závislosti na velikosti populace. Pokud některým detailům nerozumíte, hledejte vysvětlení u vyučujícího, u kolegů, pomocí Google nebo pomocí umělé inteligence. Takto chatboot vysvětlí obrat s "k--" při kreslení jedné z křivek.
def kolonizace(N,b=10,beta=1,D=1):
return b/(D*(N+beta))
def vymirani (N, S=1, a=1, k=1.5):
return a*N**(k)/S
N = np.linspace(0,10,100)
plt.plot(N,kolonizace(N, D=1),"k-",label="kolonizace, blízký ostrov")
plt.plot(N,kolonizace(N, D=2),"k--",label="kolonizace, vzdálený ostrov")
plt.plot(N,vymirani(N, S = 10),"r-",label=r"vymírání, velký ostrov")
plt.plot(N,vymirani(N, S = 2),"r--",label=r"vymírání, malý ostrov")
plt.legend()
ax = plt.gca()
ax.set(
ylim=(0,10),
xlim=(0,10),
title="Dynamika vývoje počtu druhů na ostrově",
xlabel="počet druhů",
ylabel="rychlost kolonizace a vymírání",
xticks=[],
yticks=[]
);
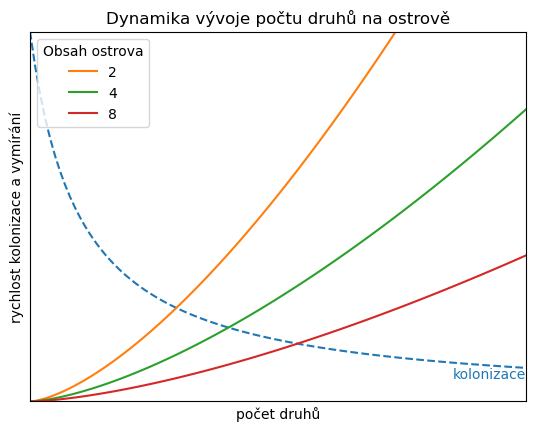
Zkusíme zafixovat rychlost kolonizace a sledovat vymírání jako funkci obsahu ostrova. Měli bychom vidět, že pro menší ostrov je větší rychlost vymírání. Rovnovážný počet druhů najdeme jako průsečík křivky vymírání s čárkovanou křivkou kolonizace. Měli bychom vidět, že první souřadnice průsečíku je pro menší ostrov menší.
# def kolonizace(N,b=10,beta=1,D=1):
# return b/(D*(N+beta))
# def vymirani (N, S=1, a=1, k=1.4):
# return a*N**(k)/S
meze = [0,10]
obsahy = [2,4,8]
N = np.linspace(*meze,100)
df = pd.DataFrame()
df["N"] = N
for S in obsahy:
df[S] = vymirani(N, k=1.5, S = S)
fig,ax = plt.subplots(1)
ax.plot(N,kolonizace(N),"--",label="_nolegend_")
df.plot(x="N", ax=ax)
ax.legend(title="Obsah ostrova", loc="upper left")
ax.text(N[-1], kolonizace(N[-1]), "kolonizace", color="C0", ha="right", va="top")
ax.set(
ylim=(0,10),
xlim=meze,
title="Dynamika vývoje počtu druhů na ostrově",
xlabel="počet druhů",
ylabel="rychlost kolonizace a vymírání",
xticks=[],
yticks=[]
);
4.3.2. Řešení diferenciální rovnice#
Nyní budeme diferenciální rovnici řešit. Použijeme bezrozměrný tvar
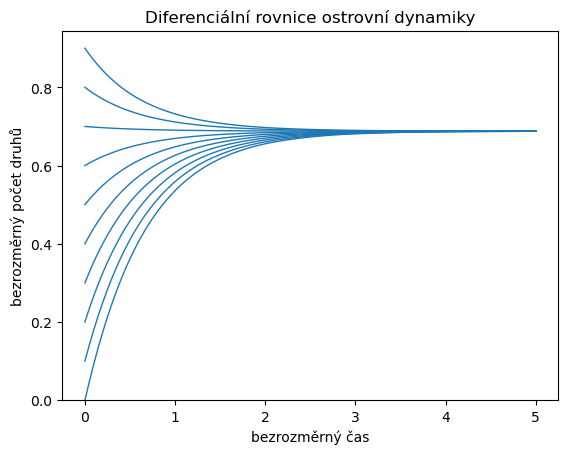
4.3.3. Závislost na počáteční podmínce#
Využijeme toho, že je možné zadat celou sadu počátečních podmínek a že nemusíme
řešit rovnici pro každou počáteční podmínku samostatně. Kromě toho zafixujeme
barvu kreslení na první barvu v sadě (C0), protože nemá smysl jednotlivá
řešení odlišovat barevně. Protože křivek je hodně, změníme tloušťku čáry.
pocatecni_podminka = np.arange(0,1,0.1)
meze = [0,5]
def rovnice(t, n, alpha=1, k=1.4):
return 1/(n+1) - alpha*n**k
t = np.linspace(*meze, 100) # definicni obor pro reseni
reseni = solve_ivp(rovnice, meze, pocatecni_podminka, t_eval=t)
fig,ax = plt.subplots(1)
ax.plot(t,reseni.y.T,color="C0",lw=1)
ax.set(
ylim=(0,None),
title="Diferenciální rovnice ostrovní dynamiky",
xlabel="bezrozměrný čas",
ylabel="bezrozměrný počet druhů",
);
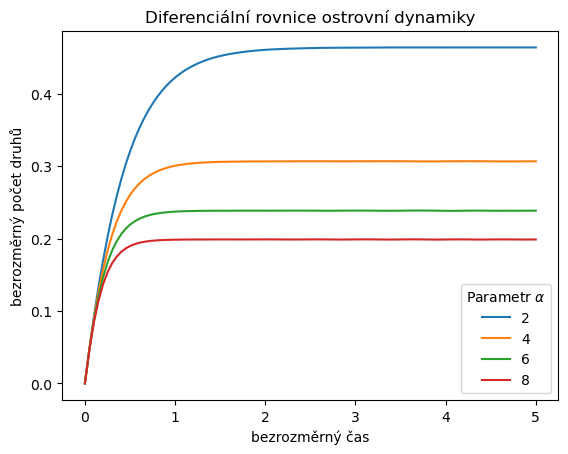
4.3.4. Závislost na parametru \(\alpha\)#
pocatecni_podminka = [0]
meze = [0,5]
alphas = [2,4,6,8]
k = 1.4
t = np.linspace(*meze, 100) # časy ve kterých určíme hodnotu řešení
def rovnice(n, alpha=1, k=1.4):
return 1/(n+1) - alpha*n**k
# Trochu jiná taktika určení řešení. Budeme ukládat rovnou hodnoty
# řešení v uvedených bodech, tj. za příkazem pro
# řešení použijeme .y[0]
reseni = [
solve_ivp(lambda t,n: rovnice(n,alpha=alpha, k=k),
meze,
pocatecni_podminka,
t_eval=t,
).y[0]
for alpha in alphas
]
df = pd.DataFrame(np.array(reseni).T, columns=alphas)
df.index = t
ax = df.plot(
title="Diferenciální rovnice ostrovní dynamiky",
xlabel="bezrozměrný čas",
ylabel="bezrozměrný počet druhů",
)
ax.legend(title=r"Parametr $\alpha$");