9. Modely konkurence populací

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

Autonomní systém v rovině

Dvourozměrné autonomní systémy můžeme analyzovat metodami založenými na klasifikaci stacionárních bodů. Typ stacionárního bodu (uzel, ohnisko, …) a jeho stabilitu poznáme u lineárního systému z vlastních čísel matice, u nelineárního z vlastních čísel Jacobiho matice.

9.1. Konkurence dvou populací

Předpokládejme, že v jisté izolované oblasti jsou přítomny dva živočišné druhy, které si vzájemně konkurují. Předpokládejme dále, že konkurence ovlivní rychlost růstu daného druhu tak, že zpomalení rychlosti růstu je přímo úměrné četnosti, s níž se jedinci jednoho druhu setkávají s jedinci druhého druhu. Nepředpokládáme přitom nic bližšího o typu této konkurence, tj. zda jedinci jednoho druhu fyzicky brání jedincům druhého druhu v přístupu k potravě, či zda je konkurence založena jenom na tom, že „ujídají ze společného krajíce“. Náš model bude zahrnovat oba typy konkurence, změna se projeví pouze ve velikosti konstanty úměrnosti, která vyjadřuje zpomalení vývoje populací vlivem konkurence.

9.1.1. Matematický model

Model konkurence

Model konkurence dvou druhů je jedním ze základních modelů usnadňujících chápání dynamiky živočišných a rostlinných společenstev.

Je-li velikost první populace vyjádřena veličinou \(x\) a velikost druhé populace veličinou \(y\), je možno systém popsat soustavou diferenciálních rovnic

\[ \begin{aligned} \frac{\mathrm dx}{\mathrm dt}={}&(a-bx)x-cxy,\\ \frac{\mathrm dy}{\mathrm dt}={}&(\alpha-\beta y)y-\gamma xy, \end{aligned} \]

kde všechno kromě \(x\),\(y\) jsou kladné reálné parametry.

Prozkoumejme strukturu tohoto systému. První členy na pravých stranách soustavy odpovídají logistickému růstu populace, pokud se tato populace nachází v prostředí osamocena. Druhé členy obsahují velikosti obou populací a odpovídají zpomalení růstu vlivem mezidruhové konkurence.

Frekvence setkávání jedinců populace \(x\) s jedinci populace \(y\) je úměrná součinu velikostí těchto populací \(xy\) a zpomalení růstu populace \(x\) vlivem těchto setkání je úměrné tomuto součinu s konstantou úměrnosti \(c\). Parametr \(c\) tedy reprezentuje sílu konkurence, tj. jaký vliv má vzájemná konkurence na růst populace \(x\). Vliv populace \(x\) na růst populace \(y\) je dán parametrem \(\gamma\), který obecně může být různý od \(c\).

Prozkoumejme ještě možná jednodruhová podspolečenstva. Pro \(y=0\) je přítomna pouze populace \(x\). První rovnice pak představuje logistickou rovnici pro vývoj populace \(x\). Nosná kapacita prostředí je \(\frac ab\).

Podobně, je-li \(x=0\), představuje druhá rovnice v soustavě logistickou rovnici pro růst populace \(y\) s nosnou kapacitou prostředí \(\frac \alpha\beta\).

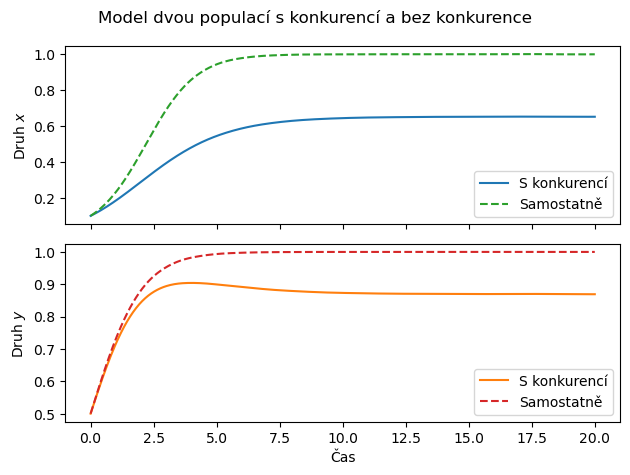
Řešení pro konkrétní sadu parametrů a konkrétní sadu počátečních podmínek najdeme stejně snadno, jako řešení jedné diferenciální rovnice. Vykreslíme si pro srovnání čárkovaně do stejného grafu i dynamiku samostatných jednodruhových populací.

Show code cell source Hide code cell source

def konkurence(t,X,a=1,b=1,c=0.4,alpha=1,beta=.2,gamma=1):
    x,y = X
    return [(a-b*x-c*y)*x, (alpha-beta*x-gamma*y)*y]

meze = [0,20]
pocatecni_podminka = [0.1,0.5]
t = np.linspace(*meze,500)

df = pd.DataFrame(index=t)
df.index.name ="čas"

for c,beta,sloupce in zip( [0.4,0] , [0.2, 0] , [["x","y"],["x0","y0"]]):
    df[sloupce] = solve_ivp(
                       lambda t,X:konkurence(t,X,c=c,beta=beta),
                       meze,
                       pocatecni_podminka,
                       t_eval=t
                       ).y.T
df.head()

	x	y	x0	y0
čas
0.000000	0.100000	0.500000	0.100000	0.500000
0.040080	0.102832	0.509608	0.103665	0.510019
0.080160	0.105715	0.519190	0.107449	0.520029
0.120240	0.108650	0.528736	0.111354	0.530024
0.160321	0.111636	0.538241	0.115380	0.539996

Show code cell source Hide code cell source

ax = df.plot(
    subplots=[("x","x0"),("y","y0")],
    legend=False,
    style=["-","-","--","--"]
)
ax[0].set(
    ylabel="Druh $x$",
)
ax[1].set(
    xlabel="Čas",
    ylabel="Druh $y$",
)

ax[0].legend(["S konkurencí", "Samostatně"])
ax[1].legend(["S konkurencí", "Samostatně"])
plt.suptitle("Model dvou populací s konkurencí a bez konkurence")
plt.tight_layout();

Pro prezentaci tabulky nebo export do Excelu je výhodnější použít hierarchické názvy sloupců.

Show code cell source Hide code cell source

sloupce = pd.MultiIndex.from_arrays(
[
    2*["s konkurencí"] + 2*["bez konkurence"],
    2*["druh x","druh y"]
])
df.columns = sloupce
df

	s konkurencí		bez konkurence
	druh x	druh y	druh x	druh y
čas
0.000000	0.100000	0.500000	0.100000	0.500000
0.040080	0.102832	0.509608	0.103665	0.510019
0.080160	0.105715	0.519190	0.107449	0.520029
0.120240	0.108650	0.528736	0.111354	0.530024
0.160321	0.111636	0.538241	0.115380	0.539996
...	...	...	...	...
19.839679	0.651708	0.869091	0.999401	0.999931
19.879760	0.651725	0.869111	0.999424	0.999934
19.919840	0.651741	0.869129	0.999447	0.999937
19.959920	0.651756	0.869147	0.999469	0.999939
20.000000	0.651771	0.869164	0.999490	0.999942

500 rows × 4 columns

9.1.2. Fázový portrét

Prozkoumáme fázový portrét. Řešení tedy budeme uvažovat jako paametrické křivky v rovině, kde na každé ose je velikost jedné z populací.

Pro nalezení nulklin přepíšeme soustavu do tvaru

\[ \begin{aligned} \frac{\mathrm dx}{\mathrm dt}={}&(a-bx-cy)x,\\ \frac{\mathrm dy}{\mathrm dt}={}&(\alpha-\beta y-\gamma x)y. \end{aligned} \]

Systém má dvě \(x\)-nulkliny

\[ \begin{aligned} &n_{1x}:\quad x=0,\\ &n_{2x}:\quad a-bx-cy=0, \end{aligned} \]

a dvě \(y\)-nulkliny

\[ \begin{aligned} &n_{1y}:\quad y=0,\\ &n_{2y}:\quad \alpha-\beta x-\gamma y=0. \end{aligned} \]

V průsečících \(x\)-nulklin a \(y\)-nulklinami nalezneme stacionární body systému.

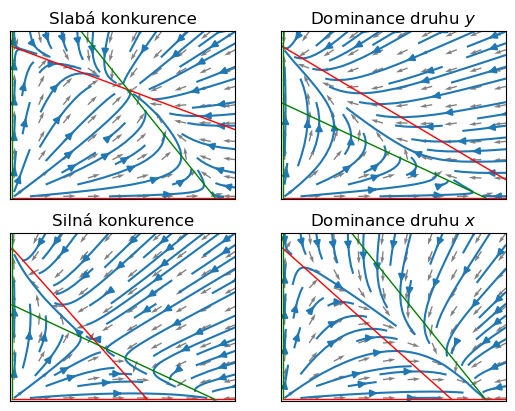
Nulklina \(n_{2x}\) je přímka procházející body \(\left[0,\frac ac\right]\) a \(\left[\frac ab, 0\right]\). Nulklina \(n_{2y}\) je přímka procházející body \(\left[\frac \alpha\gamma,0\right]\) a \(\left[0,\frac \alpha\beta\right]\). Podle vzájemné polohy těchto bodů ma osách \(x\) a \(y\) jsou možné čtyři kvalitativně odlišné případy znázorněné na obrázcích. Zeleně jsou znázorněny \(x\)-nulkliny a červeně \(y\)-nulkliny. Stacionární body jsou v průsečíku nulklin různých barev.

Show code cell source Hide code cell source

xmax, ymax = 1.1,1.1
fig,axs_square = plt.subplots(2,2)
axs = axs_square.ravel()

for i,data in enumerate([
                        [1,1,0.6,1,0.5,1],
                        [1,1,1.6,1,0.8,1],
                        [1,1,1.6,1,1.5,1],
                        [1,1,0.6,1,1.2,1],
                    ]):
    a,b,c,alpha,beta,gamma = data
    ax = axs[i]

    def konkurence(t,X):
        x,y = X
        return [(a-b*x-c*y)*x, (alpha-beta*x-gamma*y)*y]

    # Body pro kresleni
    x, y = np.meshgrid(np.linspace(0.01, xmax, 10), 
                       np.linspace(0.01, ymax, 10))

    # Komponenty vektoroveho pole
    u,v = konkurence(0,[x,y])
    M = np.sqrt(u**2+v**2) # velikost vektoru

    ax.quiver(x,y,u/M,v/M,color='gray',units='xy', angles='xy') # vykresleni s jednotkovou delkou
    ax.streamplot(x, y, u, v, density=0.5)
    #ax.set_aspect(.5) # stejne meritko na obou osach

    ax.plot([0,xmax],[0,0],color="r",lw=1)
    ax.plot([alpha/beta,0],[0,alpha/gamma],color="r",lw=1)

    ax.plot([0,0],[0,ymax],color="g",lw=1)
    ax.plot([0,a/b],[a/c,0],color="g",lw=1)

    ax.set(
        xlim=(-0.01,xmax),
        ylim=(-0.01,ymax)
    )
    ax.axes.get_xaxis().set_ticks([])
    ax.axes.get_yaxis().set_ticks([])

axs[0].set(title="Slabá konkurence")
axs[1].set(title=r"Dominance druhu $y$")
axs[2].set(title="Silná konkurence")
axs[3].set(title=r"Dominance druhu $x$");

9.1.3. Analýza stacionárních bodů

Prozkoumáme chování trajektorií v okolí stacionárních bodů.

Jacobiho matice systému je

\[J(x,y)= \begin{pmatrix} a-2bx-cy&-cx\\ -\gamma y&\alpha-2\beta y-\gamma x \end{pmatrix}.\]

Označme specifické míry růstu populací (per capita) \(m(x,y)=a-bx-cy\) a \(\mu(x,y)=\alpha-\beta y-\gamma x\).

9.1.3.1. Stacionární bod v počátku

Průsečíkem nulklin \(n_{1x}\) a \(n_{1y}\) je stacionární bod \(S_1=[0,0]\). Tento bod odpovídá stavu, kdy v prostředí není přítomna žádná z populací \(x,y\). Pronikne-li do takového prostředí malé množství jedinců populace \(x\), začnou se množit rychlostí \(m(0,0)=a\). Invazní parametr je tedy kladný a populace se uchytí. Podobně invazní parametr populace \(y\) je \(\mu(0,0)=\alpha>0\) a i populace \(y\) se v prostředí uchytí a začne množit. Jacobiho matice v bodě \(S_1\) je

\[ J(0,0)=\begin{pmatrix}a&0\\0&\alpha \end{pmatrix} \]

a protože \(\det J(0,0)=\alpha a>0\) a \(\mathop{\mathrm {Tr}} J(0,0)=a+\alpha\), je v bodě \(S_1\) nestabilní uzel nebo nestabilní ohnisko. Vzhledem k tomu, že žádná trajektorie nemůže vystoupit z prvního kvadrantu (vysvětlete proč!), jedná se o nestabilní uzel.

9.1.3.2. Stacionární body na osách

Průsečíkem nulklin \(n_{1x}\) a \(n_{2y}\) je stacionární bod \(S_2=[0,\frac \alpha\beta]\). Tento stav odpovídá tomu, že populace \(x\) se v prostředí nevyskytuje a velikost populace \(y\) je ustálena na hodnotě nosné kapacity prostředí. Jakákoliv náhodná změna populace \(y\) vede k tomu, že se systém vrátí opět do tohoto stacionárního bodu, jak víme ze studia logistické rovnice. Prozkoumejme, jak se systém chová při malých náhodných změnách populace \(x\). Invazní parametr této populace do stavu \(S_2\) je \(m\left(0,\frac \alpha\beta\right)=a-c\frac \alpha\beta=c\left(\frac ac-\frac \alpha\beta \right)\). Tento výraz je kladný pokud

(9.1)\[ \frac ac>\frac \alpha\beta, \]

tj. pokud parametr \(c\), charakterizující sílu mezidruhové konkurence, je dostatečně malý. V tomto případě se populace \(x\) uchytí a začne množit. Platí-li opačná nerovnost, bude invazní parametr populace \(x\) záporný, populace bude vymírat a systém bude dospívat zpět do stacionárního stavu \(S_2\). Jacobiho matice v bodě \(S_2\) je

\[J\left(0,\frac \alpha\beta\right)= \begin{pmatrix} a-c\frac \alpha\beta&0\\ \gamma\frac\alpha\beta&-\alpha \end{pmatrix} \]

a protože \(\det J(0,\frac\alpha\beta)=-ac\left(\frac ac-\frac\alpha\beta\right)\), je v bodě \(S_2\) sedlo, jestliže platí (9.1) a uzel nebo ohnisko jinak. Vzhledem k tomu, že trajektorie nemůže protnout osu \(y\) (proč?), nejedná se o ohnisko. Vzhledem k tvaru směrového pole se tedy jedná sedlo nebo o stabilní uzel, podle toho, zda je splněna podmínka (9.1) či nikoliv.

9.1.3.3. Stacionární bod uvnitř prvního kvadrantu

Průsečíkem nulklin \(n_{2x}\) a \(n_{1y}\) je stacionární bod \(S_3=[\frac ab,0]\). Situace je analogická jako u stacionárního bodu \(S_2\), pouze jsou vyměněny role populací \(x\) a \(y\). Systém tedy v nepřítomnosti populace \(y\) dospěje do stavu, kdy populace \(x\) se ustálí na hodnotě nosné kapacity prostředí, invazní parametr populace \(y\) do tohoto stavu je \(\mu(\frac ab,0)=\gamma\left (\frac \alpha\gamma-\frac ac\right)\) a je kladný pokud

(9.2)\[ \frac\alpha\gamma>\frac ab \]

a záporný jinak. Bod \(S_3\) je sedlo, pokud uvedená podmínka platí a stabilní uzel jinak.

Průsečík nulklin \(n_{2x}\) a \(n_{2y}\) získáme řešením soustavy rovnic

(9.3)\[ \begin{aligned} a-bx-cy&{}=0,\\ \alpha-\beta y-\gamma x&{}=0. \end{aligned} \]

Toto lze provést numericky, přímým řešením, nebo graficky. Zajímáme se přitom pouze o řešení, které se nachází v prvním kvadrantu, tj. jehož obě složky jsou nezáporné. Z náčrtů je patrné, že přímky odpovídající těmto nulklinám se protnou v prvním kvadrantu právě tehdy, když buď platí obě z nerovností (9.1), (9.2), nebo ani jedna. Označme průsečík nulklin \(S_4=(x^*, y^*)\). I když hodnoty \(x^*,y^*\) je možno explicitně vypočítat, uvidíme, že jejich znalost nebude pro vyšetřování typu stacionárního bodu důležitá. Jacobiho matice v bodě \(S_4\) je

\[ J(x^*,y^*)= \begin{pmatrix} a-2bx^*-cy^*&-cx^*\\ -\gamma y^*&\alpha-2\beta y^*-\gamma x^* \end{pmatrix}. \]

Vzhledem k tomu, že \((x^*, y^*)\) jsou řešením (9.3), platí

\[ \begin{aligned} a-bx^*-cy^*&{}=0,\\ \alpha-\beta y^*-\gamma x^*&{}=0 \end{aligned} \]

a proto

\[ J(x^*,y^*)= \begin{pmatrix} -bx^*&-cx^*\\ -\gamma y^*&-\beta y^* \end{pmatrix}. \]

Stopa Jacobiho matice je vždy záporná. Determinant Jacobiho matice je

\[ \det J(x^*,y^*)=b\beta x^*y^*-c\gamma x^*y^*=x^*y^*(b\beta-c\gamma). \]

Pokud platí (9.1) a (9.2), pak

\[ b\beta>\frac{\alpha c}a \frac{a\gamma}\alpha=c\gamma, \]

determinant Jacobiho matice je kladný a bod \(S_4\) je ohnisko nebo uzel. Vzhledem k tvaru směrového pole se nemůže jednat o ohnisko a bod je tedy stabilní uzel. Pokud neplatí ani jedna z nerovností (9.1), (9.2), je determinant Jacobiho matice naopak záporný a v bodě \(S_4\) je sedlo.

9.1.3.4. Shrnutí

• Platí-li obě z nerovností (9.1), (9.2), leží uvnitř prvního kvadrantu singulární bod, který je stabilním uzlem. Všechny trajektorie ležící v prvním kvadrantu konvergují do tohoto bodu pro \(t\to\infty\). Systém tedy vždy dospěje do stavu, kdy přežívají obě populace. Podmínky (9.1) a (9.2) jsou splněny, pokud jsou parametry \(c,\gamma\), které charakterizují mezidruhovou konkurenci, dostatečně malé. Proto tento stav budeme nazývat slabou konkurencí.

• Platí-li (9.1) a neplatí-li (9.2) nemá systém uvnitř prvního kvadrantu singulární bod a všechny trajektorie ležící uvnitř tohoto kvadrantu konvergují pro \(t\to\infty\) do stacionárního bodu \([\frac ab,0]\). V systému tedy dojde vlivem mezidruhové konkurence k vyloučení druhu \(y\) a populace druhu \(x\) se ustálí na hodnotě, odpovídající jeho nosné kapacitě prostředí. Tento stav budeme nazývat dominancí druhu \(x\).

• Platí-li (9.2) a neplatí-li (9.1), je situace podobná jako v předchozím bodě, pouze dochází ke konkurenčnímu vyloučení druhu \(x\) a jedná se tedy o dominanci druhu \(y\).

• Neplatí-li ani jedna z nerovností (9.1), (9.2), má systém uvnitř prvního kvadrantu singulární bod, který je sedlem a tedy pouze konečný počet trajektorií konverguje k tomuto bodu. Tento bod však nebude odpovídat reálnému stavu, ve kterém se může populace trvale nacházet, protože není odolný vůči náhodným perturbacím. Trajektorie, konvergující do tohoto sedlového bodu, rozdělí první kvadrant na dvě množiny, které tvoří oblasti atraktivity jednotlivých stabilních stacionárních bodů. Všechny trajektorie tedy směřují pro \(t\to\infty\) buď do stacionárního bodu \([\frac ab,0]\), nebo \([0,\frac\alpha\beta]\). V systému tedy vždy dojde ke konkurenčnímu vyloučení jednoho z druhů. Který z druhů bude vyloučen, záleží na počátečních podmínkách. Pokud jsou počáteční podmínky nastaveny tak, že trajektorie začíná v oblasti atraktivity stacionárního bodu \([\frac ab,0]\), dojde k eliminaci druhu \(y\), pokud je tomu naopak, dojde k eliminaci druhu \(x\). Nesplnění nerovností (9.1), (9.2) odpovídá tomu, že parametry mezidruhové konkurence jsou dostatečně velké, proto tento stav budeme nazývat silnou konkurencí.

Všechny typy konkurence (konkurenční vyloučení, slabá konkurence, silná konkurence) jsou v přírodě pozorovány. V ekologii zpravidla největší pozornost upoutává slabá konkurence, kdy dochází ke stabilní koexistenci. Tento jev nastává, pokud, řečeno v biologických termínech, jedinec daného druhu svou existencí konkuruje jedincům svého druhu více, než jedincům druhu jiného. V praxi to znamená, že druhy musí mít poněkud odlišné ekologické nároky (Gauseho princip). Například společně hnízdící druhy ptáků si konkurují v boji o hnízdiště. Tyto druhy mohou koexistovat, pokud mají například rozdílné složení potravy. V tomto případě jedinec konkuruje svému druhu i v boji o prostor k hnízdění i v boji o potravu, jedincům druhého druhu však konkuruje méně – pouze v boji o hnízdiště. Všimněme si ještě, že pokud vedle sebe koexistují dvě populace, součet velikostí je větší než velikost rovnovážných stavů kterékoliv osamocené populace. Dvě konkurující-si populace tedy využívají zdroje efektivněji než populace jediná.

Lze ukázat, že ke konkurenčnímu vyloučení slabšího druhu nemusí dojít, pokud druhy žijí v komplikovanějších podmínkách, než jaké jsme dosud uvažovali: například v přítomnosti třetího konkurenta, v přítomnosti predátora, v periodicky se měnícím životním prostředí, či pokud na sebe druhy reagují se zpožděním, ve fragmentovaném prostředí, kdy silnější druh neobsadí všechny fragmenty a zůstane tak volný prostor pro slabší druh.

9.2. Model konkurence tří druhů

Podobný model, jako pro konkurenci dvou druhů, je možno sestavit i pro konkurenci tří a více druhů. Matematický popis je v tomto případě poněkud obtížnější, proto se omezíme na formulaci systému diferenciálních rovnic a na některé výsledky.

Označíme-li velikost populace jednotlivých druhů veličinami \(x,y,z\), je možno model konkurence mezi těmito druhy zapsat ve tvaru

\[ \begin{aligned} \frac{\mathrm dx}{\mathrm dt}={}&(a-bx-cy-dz)x,\\ \frac{\mathrm dy}{\mathrm dt}={}&(\alpha-\beta x-\gamma y-\delta z)y,\\ \frac{\mathrm dz}{\mathrm dt}={}&(m-nx-oy-pz)z, \end{aligned} \]

kde všechny veličiny kromě \(x,y,z\) jsou kladné parametry.

Je-li v lokalitě přítomen pouze jeden druh (např. \(x\)), vyvíjí se podle logistické rovnice a velikost populace se ustálí na hodnotě dané úživností prostředí. O tom, zda do takového stavu mohou proniknout druhy \(z\) nebo \(y\) a úspěšně se začít rozmnožovat rozhodují znaménka invazních parametrů těchto populací v uvažovaném stacionárním bodě. Například populace \(y\) má ve stacionárním bodě \([\frac ab,0,0]\) invazní parametr \(\alpha-\beta \frac ab-\gamma 0-\delta 0=\beta\left(\frac \alpha\beta-\frac ab\right)\) a populace \(z\) má v tomtéž bodě invazní parametr \(n\left(\frac mn-\frac ab\right)\).

Není-li druh \(z\) ve skutečnosti v dané lokalitě přítomen, je \(z=0\) a první dvě rovnice zcela odpovídají modelu konkurence mezi dvěma populacemi \(x\) a \(y\). Podobně je možno studovat další dvojdruhová společenství \(x\),\(z\) a \(y\),\(z\). Pokud invazní parametr každého druhu, který není ve společenstvu přítomen, do stavu reprezentovaného stabilními stavy dalších dvou druhů, je kladný, systém je permanentní a velikost všech populací se udrží na nenulové hodnotě. Tato podmínka kladnosti všech invazních parametrů je však pouze dostatečná, nikoliv nutná.

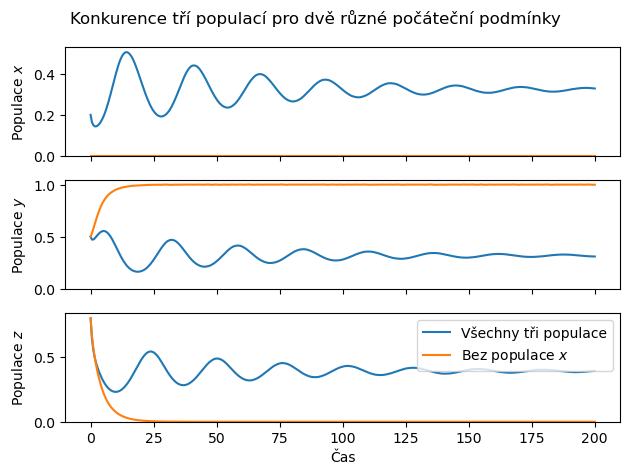
Numerickým řešením tohoto systému je možné ukázat, že při vhodném nastavení parametrů mezidruhové konkurence existuje situace, kdy libovolné dvojdruhové podspolečenství druhů \(x\),\(y\),\(z\) není permanentní a dojde ke konkurenčnímu vyloučení některého druhu a k obsazení dané lokality jediným druhem, zatímco v přítomnosti nenulového stavu všech tří populací existuje ustálený stav, charakterizující přežívání všech tří populací. V takovém případě se tedy, poněkud paradoxně, kromě konkurence jedná i o jistý druh symbiózy. Je možné, že pokud jeden z druhů náhodnými vlivy nebo neopatrným zásahem člověka vymře, nemusí toto vymření vést k posílení populací jeho konkurentů, ale někteří z konkurentů mohou vyhynout, zatímco jiní dominují.

Show code cell source Hide code cell source

meze = [0,200]
def konkurence_tri(t,X,
    a=1,b=1,c=0.4,d=1.4,
    alpha=1,beta=1.5,gamma=1,delta=0.5,
    m=1,n=0.7,o=1.2,p=1
    ):
    x,y,z = X
    return [
      (a-b*x-c*y-d*z)*x, 
      (alpha-beta*x-gamma*y-delta*z)*y,
      (m-n*x-o*y-p*z)*z
      ]

parametry = (1, 1,   0.4, 1.4,
             1, 1.5, 1,   0.5,
             1, 0.7, 1.2, 1  )

# Můžete vyzkoušet i tuto zajímavou sadu parametrů.
# parametry = (1, 1,   0.3, 1.6,
#               1, 1.8, 1,   0.2,
#               1, 0.3, 1.8, 1  )

pocatecni_podminky = [ [.2,.5,0.8],
                       [0,.5,0.8],
                     ]
t = np.linspace(*meze,400)

df = pd.DataFrame(index=t)
df.index.name = "čas"

for i,pocatecni_podminka in enumerate(pocatecni_podminky):
    df[[f"x{i}",f"y{i}",f"z{i}"]] = solve_ivp(
        lambda t,X:konkurence_tri(t,X,*parametry),
        meze,
        pocatecni_podminka,
        t_eval=t
        ).y.T
df.head()

	x0	y0	z0	x1	y1	z1
čas
0.000000	0.200000	0.500000	0.800000	0.0	0.500000	0.800000
0.501253	0.165744	0.472831	0.647708	0.0	0.530781	0.671043
1.002506	0.151107	0.471282	0.564768	0.0	0.569209	0.584107
1.503759	0.144729	0.480006	0.508911	0.0	0.609614	0.514373
2.005013	0.143258	0.493259	0.466966	0.0	0.650017	0.456115

Show code cell source Hide code cell source

ax = df.plot(
    subplots=[("x0","x1"),("y0","y1"),("z0","z1")],
    #style=["-"]*3 + ["--"]*3,
    color=["C0"]*3+["C1"]*3,
    legend=False
    )
ax[2].legend(["Všechny tři populace","Bez populace $x$"])   
ax[0].set(ylabel="Populace $x$")
ax[1].set(ylabel="Populace $y$")
ax[2].set(ylabel="Populace $z$",xlabel="Čas")
for a in ax:
    a.set(ylim=(0,None))
plt.suptitle("Konkurence tří populací pro dvě různé počáteční podmínky");     
plt.tight_layout();     

Pro export dat může být výhodnější použít popisnější názvy pro sloupce a hierarchický index.

Show code cell source Hide code cell source

sloupce = pd.MultiIndex.from_arrays(
    [
        ["Počáteční podmínka 0"]*3+["Počáteční podmínka 1"]*3,
        ["Druh x","Druh y","Druh z"]*2
    ])  
tabulka = df.copy()
tabulka.columns = sloupce
tabulka

	Počáteční podmínka 0			Počáteční podmínka 1
	Druh x	Druh y	Druh z	Druh x	Druh y	Druh z
čas
0.000000	0.200000	0.500000	0.800000	0.0	0.500000	8.000000e-01
0.501253	0.165744	0.472831	0.647708	0.0	0.530781	6.710428e-01
1.002506	0.151107	0.471282	0.564768	0.0	0.569209	5.841069e-01
1.503759	0.144729	0.480006	0.508911	0.0	0.609614	5.143729e-01
2.005013	0.143258	0.493259	0.466966	0.0	0.650017	4.561152e-01
...	...	...	...	...	...	...
197.994987	0.331982	0.310686	0.389897	0.0	1.000651	3.121549e-18
198.496241	0.331542	0.310149	0.390817	0.0	0.999512	2.819905e-18
198.997494	0.331030	0.309756	0.391773	0.0	0.998449	2.547061e-18
199.498747	0.330415	0.309473	0.392701	0.0	0.998508	2.303830e-18
200.000000	0.329714	0.309308	0.393595	0.0	0.999096	2.085541e-18

400 rows × 6 columns

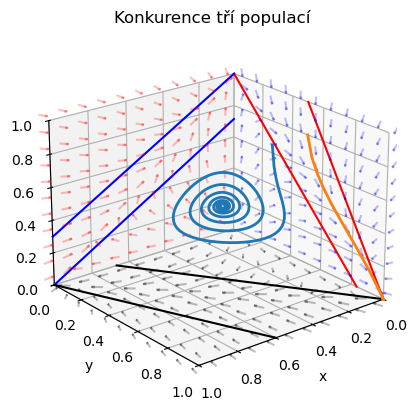
Na obrázku je schematicky zachycena jedna z možných situací. V průmětnách jsou zachyceny poměry pro jednotlivá dvojdruhová společenství. Odsud plyne, že v případě dvojdruhového společenství \(zy\) (červená rovina) dominuje druh \(y\), v případě společenství \(xz\) (modrá rovina) dominuje druh \(z\) a u společenství \(xy\) (černá rovina) dominuje druh \(x\). Na osách jsou vyznačeny stacionární body charakterizující nosnou kapacitu prostředí pro každou z populací, pokud je populace v prostředí sama. Průsečíky zaznačených přímek s osou \(x\) jsou (v pořadí od počátku) \(\frac \alpha\beta\), \(\frac ab\) a \(\frac mn\), s osou \(y\) \(\frac mo\), \(\frac \alpha\gamma\) a \(\frac ac\) a s osou \(z\) body \(\frac ad\), \(\frac mp\) a \(\frac \alpha\delta\).

Show code cell source Hide code cell source

a,b,c,d,alpha,beta,gamma,delta,m,n,o,p = parametry

fig = plt.figure()
ax = plt.axes(projection ='3d')
ax.view_init(22, 51)

body = np.array([
    [0,alpha/gamma,0,0,(alpha-delta)/gamma,1],
    [0,m/o,0,0,0,m/p],
    [b/a,0,0,0,0,a/d],
    [1,0,(m-n)/p,0,0,m/p],
    [b/a,0,0,(a-c)/b,1,0],
    [alpha/beta,0,0,0,alpha/gamma,0]
])
barvy = ["red","red","blue","blue","black","black"]
for bod,barva in zip(body, barvy):
    ax.plot3D([bod[0],bod[3]], [bod[1],bod[4]], [bod[2],bod[5]], color=barva)

ax.set_title('Konkurence tří populací')
ax.set(
    xlabel="x",
    ylabel="y",
    zlabel="z",
    xlim=(0,1),
    ylim=(0,1),
    zlim=(0,1),
)

# Make the grid
x, y, z = np.meshgrid(np.arange(0.05, 1.1, 0.1),
                      np.arange(0.05, 1.1, 0.1),
                      np.array([0]))
u, v, w = (a-b*x-c*y-d*z)*x, (alpha-beta*x-gamma*y-delta*z)*y,(m-n*x-o*y-p*z)*z
ax.quiver(x, y, z, u, v, w, length=0.05, normalize=True, color="black", alpha=0.25)

x, y, z = z, x, y
u, v, w = (a-b*x-c*y-d*z)*x, (alpha-beta*x-gamma*y-delta*z)*y,(m-n*x-o*y-p*z)*z
ax.quiver(x, y, z, u, v, w, length=0.05, normalize=True, color="blue", alpha=0.25)

x, y, z = z, x, y
u, v, w = (a-b*x-c*y-d*z)*x, (alpha-beta*x-gamma*y-delta*z)*y,(m-n*x-o*y-p*z)*z
ax.quiver(x, y, z, u, v, w, length=0.05, normalize=True, color="red", alpha=0.25)

k = df[["x0","y0","z0"]].values.T
ax.plot3D(*k, zorder=10, lw=2) 
k = df[["x1","y1","z1"]].values.T
ax.plot3D(*k, zorder=10, lw=2) 

[<mpl_toolkits.mplot3d.art3d.Line3D at 0x7ff407db2840>]

Teto příklad ukazuje, že v lokalitě obsazené větším počtem druhů, je možná koexistence druhů, které jinak koexistovat nemohou. V ekologii se zpravidla druhově rozmanitější společenství považují za stabilnější a odolnější vůči jakýmkoliv změnám.

9.3. Symbióza dvou druhů

Podobně jako jsme modelovali konkurenci dvou druhů, můžeme modelovat i symbiózu dvou druhů – situaci, kdy přítomnost jedné populace podporuje růst populace druhé. tento stav lze popsat soustavou diferenciálních rovnic obdobnou soustavě pro konkurenci, pouze změníme znaménka u členů charakterizujících vnitrodruhové působení. Studujme tedy soustavu

\[ \begin{aligned} x'={}&(a-bx)x+cxy,\\ y'={}&(\alpha-\beta y)y+\gamma xy, \end{aligned} \]

kde \(x\), \(y\) jsou velikosti jednotlivých populací a ostatní veličiny jsou kladné reálné parametry. Podobná analýza jako u modelu konkurence dvou druhů přináší následující výsledky.

• Tři stacionární body odpovídají jednomu stavu bez přítomnosti obou populací, a dvěma stavům, kdy v prostředí je přítomna pouze jedna z populací, jejíž velikost je ustálena na hodnotě kapacity prostředí. Tyto stacionární body jsou nestabilní.

• Jestliže míra symbiózy je dostatečně silná; přesněji, pokud platí

  \[ c\gamma>b\beta, \]
  pak systém nemá žádný další stacionární bod a všechny trajektorie jsou pro \(t\to\infty\) neohraničené. Tento stav odpovídá situaci, kdy míra užitku ze symbiózy převáží vliv vnitrodruhové konkurence, která jinak zastavuje růst. Protože růst obou populací není ohraničený, obě populace po přemnožení zničí své životní prostředí. V angl. literatuře charakterizuje tento stav termín „orgy of mutual beneficion“ (orgie vzájemné dobročinnosti).

• Jestliže míra symbiózy je malá, tj. jestliže platí

  \[ c\gamma<b\beta, \]
  má systém stabilní stacionární bod v prvním kvadrantu. Velikosti populací se ustálí na hodnotě, odpovídající tomuto bodu. Velikost obou populací bude převyšovat úživnou hodnotu prostředí každé z populací, populace tedy bude mít větší velikost, než jakou by měla, kdyby se v prostředí nacházela osamocena.

Další pojednání o modelech konkurence je možno nalézt například v [3] kapitola 7.4 a [16] str. 220.