Diferenciální rovnice pro pokročilejší

Pokročilejší dovedností je například odhalení, jak se rovnice chová při změně parametru.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

pocatecni_podminka = [0.1]
meze = [0,10]
lovy = [0,0.2,0.4]

def rovnice(t, x, h=0):
    """
    Logistický růst a lov konstantním úsilím, tj za jednotku času se loví stále stejné procento populace.
    """
    r = 1
    K = 1
    return r*x*(1-x/K) - h*x

t=np.linspace(*meze, 100)  # pole s rovnoměrně rozloženými hodnotami, použije se pro vodorovnou osu.
reseni = {f"h={lov:.1f}": solve_ivp(  
                lambda t,x:rovnice(t,x,h=lov),
                meze,
                pocatecni_podminka,
                t_eval=t,
                   ).y[0]
          for lov in lovy }
reseni

{'h=0.0': array([0.1       , 0.1094653 , 0.11970214, 0.13075307, 0.1426639 ,
        0.15547284, 0.1692106 , 0.18390033, 0.19955763, 0.21619058,
        0.23379968, 0.25237792, 0.27192067, 0.29240312, 0.31376227,
        0.33592782, 0.35882253, 0.38236222, 0.40645581, 0.43100527,
        0.45590567, 0.48104513, 0.50630486, 0.53155913, 0.55667531,
        0.58151381, 0.60592813, 0.62977451, 0.65297471, 0.67545965,
        0.69716532, 0.71803661, 0.73802729, 0.75710001, 0.77522631,
        0.79238663, 0.80857029, 0.82377548, 0.8380093 , 0.85128773,
        0.86363563, 0.87508675, 0.88568373, 0.8954781 , 0.90453028,
        0.91290036, 0.92060771, 0.92768877, 0.93418336, 0.94013071,
        0.94556941, 0.95053746, 0.95507225, 0.95921055, 0.96298626,
        0.96642671, 0.96955758, 0.97240355, 0.97498833, 0.97733461,
        0.97946411, 0.98139754, 0.98315846, 0.98478676, 0.98628837,
        0.98766373, 0.98891448, 0.99004346, 0.99105471, 0.99195343,
        0.99274606, 0.99344019, 0.99404464, 0.99456939, 0.99502566,
        0.99542581, 0.99578343, 0.99611329, 0.99643137, 0.99675461,
        0.99707156, 0.99736602, 0.99763723, 0.9978848 , 0.99810862,
        0.99830892, 0.99848625, 0.99864147, 0.99877577, 0.99889065,
        0.99898796, 0.99906983, 0.99913874, 0.99919747, 0.99924914,
        0.99929717, 0.99934533, 0.99939768, 0.99945477, 0.99950713]),
 'h=0.2': array([0.1       , 0.10728758, 0.11501758, 0.12320444, 0.13186311,
        0.14100553, 0.15064066, 0.16077447, 0.17140994, 0.18254704,
        0.19418277, 0.20631111, 0.21892394, 0.23202044, 0.24557791,
        0.25956483, 0.27394793, 0.28869215, 0.30376065, 0.31911482,
        0.33471427, 0.35051682, 0.36647854, 0.38255369, 0.39869478,
        0.41485253, 0.43097587, 0.44701199, 0.46290626, 0.47860229,
        0.49404192, 0.50916635, 0.52394187, 0.53834452, 0.55234917,
        0.56593348, 0.57907786, 0.59176545, 0.60398217, 0.61571668,
        0.6269604 , 0.6377075 , 0.64795491, 0.65770232, 0.66695215,
        0.6757096 , 0.68398261, 0.69178189, 0.69912087, 0.70601578,
        0.71248558, 0.71855197, 0.72423944, 0.72957519, 0.73458815,
        0.73928621, 0.74367832, 0.74777887, 0.75160218, 0.75516248,
        0.75847391, 0.7615505 , 0.76440621, 0.76705491, 0.76951036,
        0.77178624, 0.77389614, 0.77585355, 0.77767188, 0.77936263,
        0.78093251, 0.78238805, 0.78373571, 0.78498187, 0.78613285,
        0.78719489, 0.78817417, 0.78907677, 0.78990871, 0.79067593,
        0.79138431, 0.79203965, 0.79264766, 0.79321363, 0.79373976,
        0.79422767, 0.79467915, 0.79509601, 0.79548011, 0.79583333,
        0.79615761, 0.79645491, 0.79672722, 0.7969766 , 0.79720511,
        0.79741486, 0.79760801, 0.79778674, 0.79795326, 0.79810985]),
 'h=0.4': array([0.1       , 0.10515303, 0.11051269, 0.11608123, 0.12186067,
        0.12785216, 0.13405595, 0.1404714 , 0.14709699, 0.15393029,
        0.160968  , 0.16820591, 0.17563892, 0.18326251, 0.1910776 ,
        0.199073  , 0.2072352 , 0.21555054, 0.22400528, 0.23258553,
        0.24127731, 0.25006648, 0.25893882, 0.26787998, 0.27687549,
        0.28591075, 0.29497105, 0.30404157, 0.31310736, 0.32215336,
        0.33116437, 0.34012509, 0.34902011, 0.35783387, 0.36655073,
        0.37515489, 0.38363047, 0.39196144, 0.40013167, 0.40812725,
        0.41594641, 0.42358392, 0.43103416, 0.43829213, 0.44535344,
        0.45221429, 0.4588715 , 0.46532249, 0.4715653 , 0.47759855,
        0.48342149, 0.48903396, 0.49443643, 0.49962994, 0.50461618,
        0.50939741, 0.5139765 , 0.51835696, 0.52254287, 0.52653892,
        0.53035043, 0.53398331, 0.53744407, 0.54073984, 0.54387835,
        0.54686794, 0.54971755, 0.55243661, 0.55502999, 0.5575002 ,
        0.55985069, 0.56208495, 0.56420653, 0.56621904, 0.56812612,
        0.56993148, 0.57163888, 0.57325211, 0.57477504, 0.57621159,
        0.5775657 , 0.57884139, 0.58004274, 0.58117384, 0.58223888,
        0.58324207, 0.58418768, 0.58508004, 0.58592352, 0.58672254,
        0.58748158, 0.58820297, 0.58888393, 0.5895263 , 0.59013213,
        0.59070343, 0.59124209, 0.59174994, 0.59222874, 0.59268012])}

df = pd.DataFrame(reseni, index=t) # vytvoření tabulky
df.index.name = "Čas"
df

	h=0.0	h=0.2	h=0.4
Čas
0.00000	0.100000	0.100000	0.100000
0.10101	0.109465	0.107288	0.105153
0.20202	0.119702	0.115018	0.110513
0.30303	0.130753	0.123204	0.116081
0.40404	0.142664	0.131863	0.121861
...	...	...	...
9.59596	0.999297	0.797415	0.590703
9.69697	0.999345	0.797608	0.591242
9.79798	0.999398	0.797787	0.591750
9.89899	0.999455	0.797953	0.592229
10.00000	0.999507	0.798110	0.592680

100 rows × 3 columns

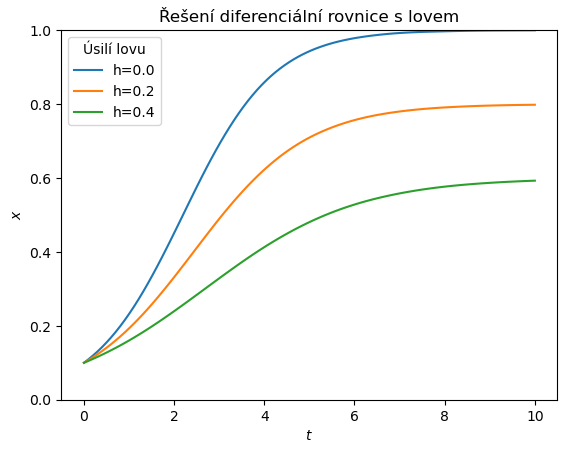
fig,ax = plt.subplots(1)
df.plot(ax=ax)

<Axes: xlabel='Čas'>

ax.set(
    ylim = (0,1),
    title = "Řešení diferenciální rovnice s lovem",
    xlabel=r"$t$",
    ylabel=r"$x$",
)
ax.legend(title="Úsilí lovu")
fig