Ctrl+K

Práce s funkcemi

3. Práce s funkcemi#

Zopakujeme si vytváření tabulky a kreslení dat z tabulky z minulého cvičení. Poté si ukážeme, jak je možné definovat novou funkci.

3.1. Obrázek se třemi funkcemi#

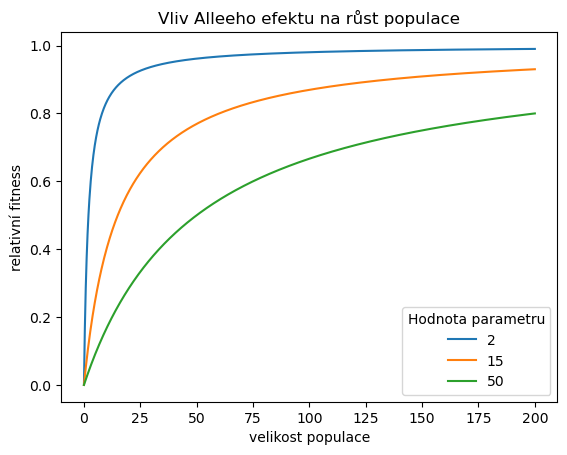
V článku Consequences of the Allee effect for behaviour, ecology and conservation (Stephens, Sutherland, 1999) autoři pracují s modelem Alleeho efektu v populaci a modelují jej funkcí

\[p=\frac{n}{n+\theta}\]
pro hodnoty \(\theta\) postupně 2,15 a 50. Pokusíme se překreslit jejich obrázek této funkce pro dané tři parametry.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

x = np.linspace(0,200,1000)
seznam_parametru = [2,15,50]
df = pd.DataFrame(index=x)
for parametr in seznam_parametru:
    df[parametr] = x/(parametr+x)

ax = df.plot()
ax.set(
    title="Vliv Alleeho efektu na růst populace",
    xlabel="velikost populace",
    ylabel="relativní fitness")
plt.legend(title = "Hodnota parametru")    

<matplotlib.legend.Legend at 0x7f6c90c07da0>
../_images/2577570bc39c02034abac80f36e247c9bce8f5a7f70c9d5d88c5bddb8f75f18d.png

Není ani nutné tvořit tabulku sloupec po sloupci (operace je pomalá), ale je možné využít datový typ dictionary. Každý si může vybrat, co je pro něj čtivější.

x = np.linspace(0,200,1000)
seznam_parametru = [2,15,50]
df = pd.DataFrame({parametr : x/(parametr+x) for parametr in seznam_parametru}, index=x)

ax = df.plot()
ax.set(
    title="Vliv Alleeho efektu na růst populace",
    xlabel="velikost populace",
    ylabel="relativní fitness")
plt.legend(title = "Hodnota parametru")    

<matplotlib.legend.Legend at 0x7f6c90b42660>
../_images/2577570bc39c02034abac80f36e247c9bce8f5a7f70c9d5d88c5bddb8f75f18d.png

3.2. Definice vlastní funkce#

Delší úseky kódu zpravidla kumulujeme do funkcí. Tím se výsledný skript zjednoduší a je lépe srozumitelný.

Příklad definice funkce s povinnými a nepovinnými parametry

def mocnina(zaklad,n=2):
    """
    Funkce vrací n-tou mocninu zadaného čísla. 
    Pokud není hodnota n zadána, použije se 2.
    
    Důležitá je i dokumentace k funkci. V době pořizování kódu zpravidla chápeme, 
    co funkce dělá a jak funguje, ale pokud se k funkci vrátíte za několik
    let, može u komplikovanějších funkcí být problém. Také je dobré udržovat 
    dokumentaci funkce aktuální pro případné spolupracovníky nebo následovníky.
    """
    vysledek = zaklad**n
    return vysledek

Ukázky volání. V prvním případě se použije přednastavená hodnota exponentu, ve druhém případě se umocňuje na čtvrtou.

mocnina(5)

25

mocnina(5,n=4)

625

Následující volání je zapoznámkováno, protože vyvolá chybu. Nebyl zadán základ a ten je povinným parametrem. Můžete zrušit zapoznámkování a příkaz si zkusit.

#mocnina()

Pokud zadáváme všechny volitelné parametry, není nutné psát jejich jméno. Níže je \(6^7\) (šest na sedmou).

mocnina(6,7)

279936

# Nápověda
?mocnina

3.3. Volitelná část, samostudium, pro zájemce#

Vyzkoušejte si samostatně, pokud jste rychlejší než jak běží výuka. Ukazuje, jak vyřešit model založený na derivacích primitivními prostředky. To se někdy hodí, ale my se příště naučíme používat vyspělejší nástroje.

3.3.1. Rovnice ochlazování#

Studujme úlohu ochlazování kávy o teplotě \(T\) z počáteční teploty \(T_0\) v prostředí s teplotou \(T_\infty\) a koeficientem \(k\) charakterizujícím intenzitu tepelné výměny podle Newtonova zákona tepelné výměny. Matematický model děje má tvar ve tvaru

\[\frac{\mathrm dT}{\mathrm dt} = - k (T-T_\infty), \quad T(0)=T_0.\]
Pokusíme se odhadnout po malých krůčcích chování řešení. Uvnitř každého krůčku budeme rychlost považovat za konstantní a změnu teploty určíme jako součin

rychlosti a času (délky časového intervalu).

3.3.2. Jednoduchá numerická simulace#

Vyřešíme rovnici pro počáteční teplotu \(T_0=100^\circ\mathrm{C}\), okolní teplotu \(T_\infty=20^\circ\mathrm{C}\), koeficient přímé úměrnosti \(k=0.1 \,\mathrm{min}^{-1}\) a časový krok \(\Delta t=2\,\mathrm {min}.\)

Data budeme sestavovat do tabulky s časem a teplotou. První řádek je dán počáteční teplotou, časový sloupec je dán časovým krokem a musíme dopočítat teplotu.

t

T

0

100

2

4

6

8

…

  • Výpočet teploty v čase \(2\,\mathrm {min}\)

    • Rozdíl teplot je

      \[\Delta T = 100^{\circ}\mathrm C - 20^{\circ}\mathrm C = 80^{\circ}\mathrm C.\]

    • Rychlost ochlazování je

      \[k(T-T_\infty)=0.1\,\mathrm{min}^{-1} \times 80^{\circ}\mathrm C = 8^{\circ}\mathrm C/\mathrm{min}.\]

    • Změna teploty je

      \[\Delta T = - k (T-T_\infty)\Delta t = - 8^{\circ}\mathrm C/\mathrm{min} \times 2\,\mathrm {min} = -16^{\circ}\mathrm C.\]

    • Teplota v čase \(t=2\,\mathrm{min}\) je součtem teploty v předešlém čase a změny teploty, tj.

      \[T(2) = T(0)+\Delta T = 100^{\circ}\mathrm C - 16^{\circ}\mathrm C = 84^{\circ}\mathrm C.\]

      Nová tabulka je následující

      t

      T

      0

      100

      2

      84

      4

      6

      8

      …

  • Výpočet teploty v čase \(4\,\mathrm {min}\)

    • Rozdíl teplot je

      \[\Delta T = 84^{\circ}\mathrm C - 20^{\circ}\mathrm C = 64^{\circ}\mathrm C.\]

    • Rychlost ochlazování je

      \[k(T-T_\infty)=0.1\,\mathrm{min}^{-1} \times 64^{\circ}\mathrm C = 6.4^{\circ}\mathrm C/\mathrm{min}.\]

    • Změna teploty je

      \[\Delta T = - k (T-T_\infty)\Delta t = - 6.4^{\circ}\mathrm C/\mathrm{min} \times 12\,\mathrm {min} = -12.8^{\circ}\mathrm C.\]

    • Teplota v čase \(t=4\mathrm{min}\) je součtem teploty v předešlém čase a změny teploty, tj.

      \[T(4) = T(2)+\Delta T = 84^{\circ}\mathrm C - 12.8^{\circ}\mathrm C = 71.2^{\circ}\mathrm C.\]

      Nová tabulka je následující

      t

      T

      0

      100

      2

      84

      4

      71.2

      6

      8

      …

  • Analogicky pokračujeme a dopočítáváme teplotu v dalších časech.

3.3.3. Numerická simulace po krocích konečné délky a srovnání s přesným řešením#

# Nastavení parametrů
tmin = 0
tmax = 20
N = 11
k = 0.1
T0 = 100
T_inf = 20

# Pomocné proměnné
t = np.linspace(tmin,tmax,N) # časová osa pro simulaci
dt = t[1]-t[0]

# Počáteční nastavení
T = np.zeros(N)  # pole pro ukládání teplot
T[0] = T0  # počáteční teplota

# Simulace po časových krocích
for i in range(1,N):
    rozdil_teplot = T[i-1] - T_inf
    rychlost_ochlazovani = k*rozdil_teplot
    zmena_teploty = - dt*rychlost_ochlazovani
    T[i] = T[i-1] + zmena_teploty

# Uložení do tabulky
df = pd.DataFrame(index=t)
df["T"] = T
df.head()
T
0.0 100.000
2.0 84.000
4.0 71.200
6.0 60.960
8.0 52.768

V tomto případě máme k dispozici i analytické řešení. To má tvar

\[T(t)=T_\infty + (T_0-T_\infty)e^{-kt}.\]

# Analytické přesné řešení
df["analyticky"] = T_inf + (T0-T_inf)*np.exp(-k*t)   
    
# Vykreslení tabulky    
df.plot()
plt.gca().set(
    xlabel="čas",
    ylabel="teplota",
    title="Ochlazování rychlostí úměrnou teplotnímu rozdílu",
    ylim=(0,None)
)
plt.legend(['numericky','analyticky'],title="Výpočet");
../_images/cbbfe7574c8b7139f87b91fdbf5e68037bdf9792b7dac7cd895764522b389f2a.png

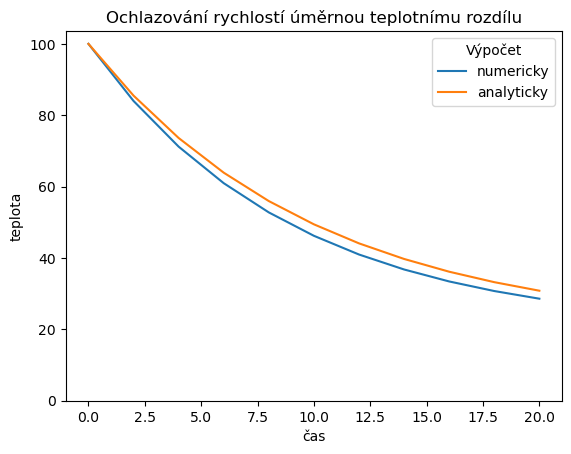
Abychom mohli pohodlně řešit modely pro různé parametry, můžeme příkazy z buňky, kde se v cyklu for počítají teploty pro jednotlivé okamžiky, seskupit do funkce a poté volat jedním příkazem. Modifikace spočívá v následujícím.

  • Definice hlavičky funkce a popis činnosti funkce. Hlavička obsahuje volitelné parametry s přednastavenými hodnotami.

  • Odsazení bloku s tělem funkce (označit blok a všechny řádky posunout naráz tabelátorem).

  • Klíčové slovo return definující výstup.

def numericke_reseni(
    t = np.linspace(0, 10, 11),
    k = 0.5,
    T0 = 100,
    T_inf = 20,
):
    """
    Naivní simulace Newtonova modelu ochlazování. Derivace je nahrazena
    dopřednou diferencí.

    Na vstupu funkce jsou volitelné parametry nastavující časový interval
    pro simulaci, dělení intervalu udávající jemnost skoků, koeficient 
    úměrnosti, počáteční teplota a koncová teplota.

    Výstupem je pole teplot.
    """

    # Počáteční nastavení
    T = np.full_like(t,T0)  # pole pro ukládání teplot a počáteční teplota

    # Simulace po časových krocích
    for i in range(1,len(T)):
        rozdil_teplot = T[i-1] - T_inf
        rychlost_ochlazovani = k*rozdil_teplot
        dt = t[i] - t[i-1]
        zmena_teploty = - dt*rychlost_ochlazovani
        T[i] = T[i-1] + zmena_teploty

    return T

Ukázka volání, všechny parametry necháme na defaultních hodnotách.

numericke_reseni()

array([100.      ,  60.      ,  40.      ,  30.      ,  25.      ,
        22.5     ,  21.25    ,  20.625   ,  20.3125  ,  20.15625 ,
        20.078125])

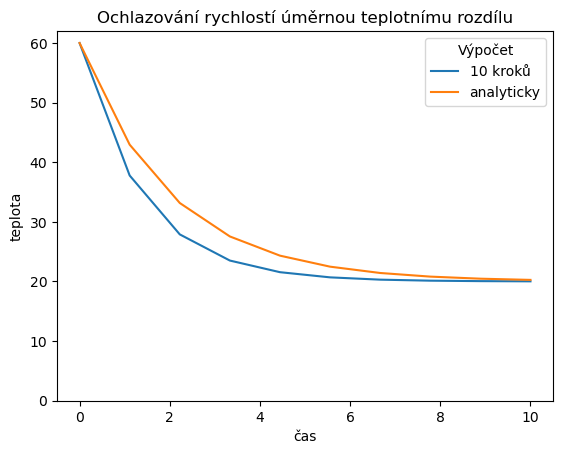
Úkol Experimentujte s počtem bodů \(N\) a tím i s délkou kroku. Sledujte hladkost numerického řešení a jeho odchylku od přesného analytického řešení.

V praxi musíme mít krok dostatečně malý, aby řešení bylo hladké a přesné, ale ne moc malý, aby nás to nestálo hodně paměti, výpočetního výkonu, času a aby nehrozilo, že se při mnoha výpočtech akumulují zaokrouhlovací chyby. Zpravidla nám toto obstarají procedury pro řešení automaticky.

# Měňte délku kroku a sledujte výstup (méně zdatní), nebo vykreslete do jednoho
# obrázku průběh pro více kroků (zdatnější - stačí opakovat tři řádky s
# jinou hodnotou N, s výpočtem řešení a vykreslením)

# Nastavení parametrů
k = 0.5
t = np.linspace(0, 10, 10)
T_inf = 20
T0 = 60


# Numerické řešení
r = numericke_reseni(k=k, t=t, T0=T0,  T_inf=T_inf)  # vyřešení modelu
plt.plot(t,r, label=f"{len(t)} kroků")     # vykreslení řešení

# Analytické řešení
plt.plot(t,T_inf + (T0-T_inf)*np.exp(-k*t), label="analyticky")

# Úpravy grafu
ax = plt.gca()              # uložení souřadné soustavy do vlastní proměnné pro kosmetiku
ax.set(                     # modifikace souřadné soustavy, kosmetické úpravy
    xlabel="čas",
    ylabel="teplota",
    title="Ochlazování rychlostí úměrnou teplotnímu rozdílu",
    ylim=(0,None)
)
plt.legend(title="Výpočet");
../_images/f6abd83a4ab006c8bd9e637474830cbd44bbe2ffa1a13026aa9bc9ff59a7ead6.png

3.3.4. Simulace pro více počátečních podmínek#

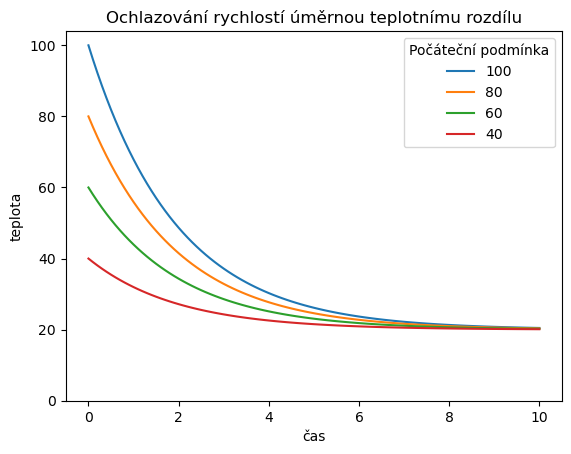
Vyjdeme z předchozí simulace, ale novou simulaci spustíme v cyklu. Jeden průběh cyklu pro každou počáteční podmínku. Výstup budeme ukládat do nové tabulky a tu potom vykreslíme.

# Tip: vygenerovaný obrázek nepotřebuje legendu ani změnu barev. Zkuste legendu
# vypnout a zakreslit všechny křivky stejnou barvou. Například barvou C0
# (základní barva pro první křivku obrázku).
# https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.plot.html
# https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html

# Příprava proměnných
T0_seznam = [100, 80, 60, 40] 
t = np.linspace(0,10,101)
df = pd.DataFrame(index=t, columns=T0_seznam)

# Výpočet
for T0 in T0_seznam:
    df[T0] = numericke_reseni(T0=T0, t=t)

# Vykreslení tabulky    
ax = df.plot()

# Kosmetika
ax.set(
    xlabel="čas",
    ylabel="teplota",
    title="Ochlazování rychlostí úměrnou teplotnímu rozdílu",
    ylim=(0,None)
)
plt.legend(title="Počáteční podmínka"); # nadpis pro legendu
../_images/737dd2ca4eeb476664048f79adc9bd3bf1085e1bd2af805b08633dc56fc8bda9.png

3.3.4.1. Úkol: simulace pro měnící se koeficient úměrnosti#

Udělejte simulaci s jednou počáteční podmínkou a měnící se hodnotu koeficientu \(k\). Nakopírujte si sem předchozí buňku a modifikujte tak, aby byla počáteční podmínka pořád stejná a měnil se koeficient \(k\). Musíte sestavit seznam hodnot pro proměnnou \(k\), změnit cyklování a změnit jméno sloupce v tabulce tak, aby zachycovalo hodnotu \(k\).

# Jako výchozí sem nakopírujte obsah buňky, která kreslí řešení pro různé
# počáteční podmínky. Tento kód modifikujte tak, aby počáteční podmínka byla
# stále stejná, ale měnila se hodnota k.

3.3.5. Simulace pro model se zpožděním#

Uvedené simulace jsou naivní metodou řešení úlohy modelující pomocí derivací nějaký proces. Pro řešení modelů s derivacemi existují mnohem vyspělejší metody, které si představíme příště. V praxi se zpravidla spoléháme na tyto metody, které jsou naprogramované profesionály.

Dovednost umět si implementovat jednoduchý řešič může sloužit pro orientační první nástřel výpočtu, nebo při potřebě řešení nějaké speciální úlohy. Jedním takovým speciálním postupem může být snaha započítat do rovnice ochlazování zpoždění. V takovém případě rychlost změny není dána aktuálními hodnotami, ale hodnotami ve minulosti. To by mohlo odpovídat regulaci teploty, kdy se změna v nastavení neprojeví okamžitě. Všichni takovou situaci známe při nastavování teploty ve sprše.

Model ochlazování se zpožděním \(\theta\) má tvar

\[\frac{\mathrm dT}{\mathrm dt} = - k (T(t-\theta)-T_\infty), \quad T(0)=T_0\]
a při numerickém řešení je jediný rozdíl v tom, že rychlost nestanovujeme podle teploty na předešlém řádku tabulky, ale používáme některý z předešlých řádků, v závislosti na velikosti zpoždění.

def numericke_reseni_se_zpozdenim(  # !!! jiné jméno funkce
    t = np.linspace(0, 10, 11),
    k = 0.5,
    T0 = 100,
    T_inf = 20,
    zpozdeni = 0     # !!! další parametr
):
    """
    Stejná funkce jako numericke_reseni s dodatečným parametrem pro zpoždění.
    Rozdíly jsou vyznačeny třemi vykřičníky.
    """
    N = len(t)

    # Počáteční nastavení
    T = np.zeros(N)  # pole pro ukládání teplot
    T[0] = T0        # počáteční teplota

    # Simulace po časových krocích
    for i in range(1,N):
        rozdil_teplot = T[max(0,i-1-zpozdeni)] - T_inf
        rychlost_ochlazovani = k*rozdil_teplot
        dt = t[i] - t[i-1]
        zmena_teploty = - dt*rychlost_ochlazovani
        T[i] = T[i-1] + zmena_teploty

    return T 

seznam_zpozdeni = [0, 10, 50, 100, 200]
t = np.linspace(0,10,1001)
df3 = pd.DataFrame(index=t, columns=seznam_zpozdeni)

for zpozdeni in seznam_zpozdeni:
    df3[zpozdeni] = numericke_reseni_se_zpozdenim(zpozdeni=zpozdeni, t=t)

df3
0 10 50 100 200
0.00 100.000000 100.000000 100.000000 100.000000 100.000000
0.01 99.600000 99.600000 99.600000 99.600000 99.600000
0.02 99.202000 99.200000 99.200000 99.200000 99.200000
0.03 98.805990 98.800000 98.800000 98.800000 98.800000
0.04 98.411960 98.400000 98.400000 98.400000 98.400000
... ... ... ... ... ...
9.96 20.543098 20.414553 20.067920 20.022809 33.232923
9.97 20.540383 20.412368 20.067433 20.022420 33.150496
9.98 20.537681 20.410194 20.066950 20.022033 33.067710
9.99 20.534992 20.408032 20.066471 20.021650 32.984570
10.00 20.532317 20.405881 20.065994 20.021271 32.901082

1001 rows × 5 columns

df3.plot()
plt.legend(title="Zpoždění")
plt.title("Rovnice ochlazování se zpožděním")

Text(0.5, 1.0, 'Rovnice ochlazování se zpožděním')
../_images/93ff66399261e60bb0aa4ba3469723b7010d38fea3b8f4bb25acc6623933f55b.png

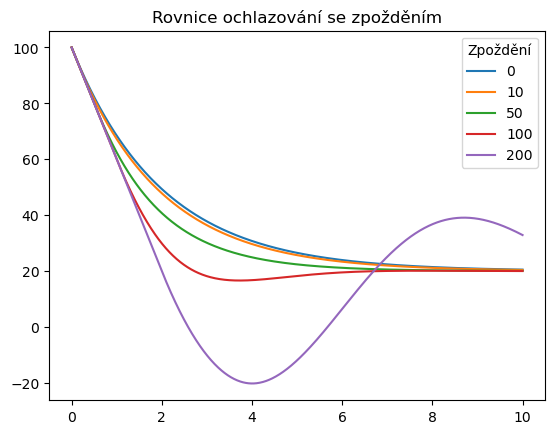
Úkol Předchozí buňky vytvoří tabulku s daty a poté vykreslí graf. To dá přehled o tom, že opravdu vzniká tabulka tak jak má. Pokud chceme sledovat, jaký mají změny dalších parametrů vliv na graf, je lepší obě buňky spojit, aby se generování tabulky i grafu spouštělo současně. Vyzkoušete to. Například tak, že se nastavíte na horní buňku a stisknete Shift+M. (Pozor na to, bez shiftu byste buňku přepnuli na textovou.)

Obsah