4. Autonomní diferenciální rovnice

Co se dozvíte v tomto textu

V tomto textu se budeme věnovat diferenciálním rovnicím, kde rychlost vývoje sledované veličiny nezávisí explicitně na čase, ale jenom na veličině samotné a na parametrech prostředí. Naprostá většina modelů splňuje tyto požadavky. Důsledkem nezávislosti na čase je jistá jednoduchost při kvalitativním popisu chování řešení.

Důležitým reprezentantem autonomních diferenciálních rovnic je logistická rovnice, která bývá výchozím kamenem při studiu rostlinných a živočišných populací a označení parametrů z této rovnice písmeny \(r\) a \(K\) dalo dokonce název základním životním strategiím živočichů i rostlin.

Foto: Albatros (Diomedea exulans) v letu. Tento pták je představitelem K-stratégů. Autor JJ Harrison , https://wikimedia.org.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

Diferenciální rovnice

\[ \frac{\mathrm dx}{\mathrm dt}=f(x)\]

s neznámou funkcí \(x(t)\) proměnné \(t\) se nazývá autonomní, nebo též nezávislá na čase. Proměnná \(t\) se nazývá čas.

Rovnici je možné řešit analytickou cestou. My se nebudeme zaměřovat na hledání analytického tvaru obecného řešení, ale pokusíme se popsat chování řešení, aniž bychom tato řešení znali. Pokusíme se s co nejmenší námahou říct, jak se budou řešení chovat.

• Je-li \(f(x_0)=0\), je konstantní funkce \(x(t)=x_0\) řešením rovnice. Protože derivace konstantní funkce je nula, vidíme, že řešením rovnice

  \[f(x)=0\]
  obdržíme všechna konstantní řešení rovnice. Tato konstantní řešení se nazývají stacionární body.

• Stacionární body a jim odpovídající konstantní řešení představují rovnovážný stav. Často nás zajímá, jestli při vychýlení z tohoto rovnovážného stavu má systém tendenci se vrátit do původního stavu, nebo se od původního stavu dále odchylovat.

• Pokud se při malém vychýlení z rovnovážného stavu systém do tohoto stavu vrací, mluvíme o stabilním stacionárním bodu.

• Pokud se systém po malé výchylce do tohoto rovnovážného stavu nevrací, ale vyvíjí se k dalšímu stacionárnímu bodu nebo neohraničeně, mluvíme o nestabilním stacionárním bodu.

Následující věta umožní odlišit stabilní a nestabilní stacionární body. Protože v přírodě dochází k drobným perturbacím neustále, udává vlastně, které stacionární stavy jsou realizovatelné a můžeme je v přírodě pozorovat a které jsou prakticky nerealizovatelné.

Věta (Stabilita konstantních řešení)

Jestliže platí \(f(x_0)=0\), je konstantní funkce \(x(t)=x_0\) konstantním řešením rovnice

\[\frac{\mathrm dx}{\mathrm dt}=f(x).\]

Toto řešení je stabilní pokud funkce \(f\) v bodě \(x_0\) klesá a nestabilní pokud funkce \(f\) v bodě \(x_0\) roste.

Protože funkce \(f\) má ve stacionárním bodě nulovou funkční hodnotu, můžeme růst nebo pokles této funkce odhalit i ze znaménka. Pokud se znaménko funkce ve stacionárním bodě mění z kladného na záporné, potom funkce klesá. V opačném případě roste.

Pravá strana bývá často rozdílem dvou faktorů, které působí proti sobě v tom smyslu, že jeden definuje rychlost růstu a druhý rychlost poklesu sledované veličiny. V takovém případě se hodí následující důsledek předchozí věty.

Důsledek (Stabilita konstantních řešení rovnice s rozdílem na pravé straně)

Jestliže platí \(f(x_0)=g(x_0)\), je konstantní funkce \(x(t)=x_0\) konstantním řešením rovnice

\[\frac{\mathrm dx}{\mathrm dt}=f(x)-g(x).\]

Toto řešení je stabilní pokud je funkce funkce \(f(x)-g(x)\) kladná v levém okolí a záporná v pravém okolí bodu \(x_0\). V případě opačných znamének je tento bod nestabilní.

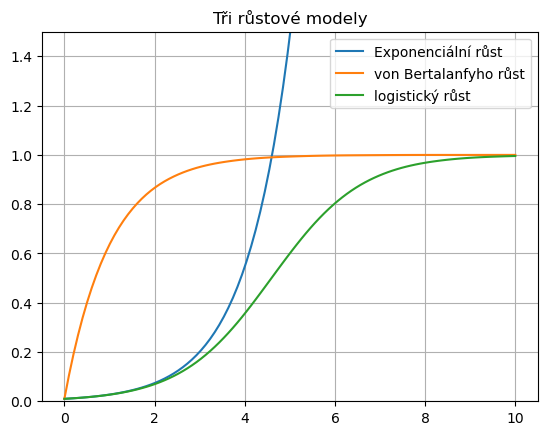
4.1. Exponenciální růst

Nejjednodušším modelem růstu populace je model vyjadřující situaci, kdy rychlost růstu je úměrná velikosti populace. Takový růst je popsán diferenciální rovnicí

\[\frac{\mathrm dx}{\mathrm dt}=kx \]

a jeho analytickým řešením vyhovujícím podmínce \(x(0)=x_0\) je funkce

\[x(t)=x_0 e^{kt}.\]

Model exponenciálního růstu je vhodný pro svou jednoduchost, ale nemůže popisovat dlouhodobý vývoj populace, protože při značné velikosti populace nedokáže daná lokalita populaci uživit. Model se nazývá Malthusův model a je použitelný pouze v krátkých časových intervalech a v situacích, kdy se neprojeví vnitrodruhová konkurence.

4.2. Von Bertalanffyho růst

Dalším modelem růstu je model, kdy je růst omezen a rychlost růstu je úměrná vzdálenosti vzdálenosti od horní hranice. Původně byl formulován pro růst jedinců, kteří se mohou dožívat maximální výšky \(L_\infty\). Podle tohoto modelu je výška \(L\) dána vztahem

\[\frac{\mathrm dL}{\mathrm dt}=k(L_\infty-L)\]

resp.

\[\frac{\mathrm dL}{\mathrm dt}=k_0\left(1-\frac{L}{L_\infty}\right),\]

kde \(k_0=\frac{k}{L_\infty}.\) Analytickým řešením modelu s počáteční podmínkou \(L(0)=L_0\) je funkce

\[L(t)=L_\infty + (L_0-L_\infty)e^{-kt}.\]

Tento vztah ukazuje, že rozdíl délky a cílové délky se exponenciálně snižuje.

Kromě jedinců rostoucích rychlostí úměrnou množství chybějícímu do maximální velikosti tato rovnice popisuje i procesy, kdy změnu sledované veličiny způsobují dva faktory: růst konstantní rychlostí a pokles rychlostí úměrnou velikosti. Potom má totiž rovnice tvar

\[\frac{\mathrm dx}{\mathrm dt} = \alpha -\beta x\]

a po vytknutí konstanty \(\alpha\) nebo \(\beta\) dospíváme (až na označení) k rovnicím výše. Tento růst například odpovídá sledování množství enzymů nebo bílkovin, které jsou produkovány konstantní rychlostí a degradují rychlostí úměrnou množství, viz [2] kapitola 1.4.

4.3. Logistický růst

Modelem pro růst populací v prostředí s nosnou kapacitou prostředí, který je všeobecně přijímán jako vhodný kompromis mezi přesností popisu a matematickou jednoduchostí je Verhulst-Pearlův model růstu, vycházející z předpokladu, že rychlost růstu populace v prostředí s omezenou nosnou kapacitou je úměrná velikosti této populace a volnému místu v životním prostředí, nejčastěji vyjádřenému procentem z nosné kapacity. Pokud nosná kapacita prostředí je \(K\) a specifická rychlost růstu bez započtení konkurence \(r\), má model tvar

\[\frac{\mathrm dx}{\mathrm dt}=rx\left(1-\frac xK\right)\]

při vyjádření rychlosti růstu a

\[\frac 1x \frac{\mathrm dx}{\mathrm dt}=r\left(1-\frac xK\right)\]

při vyjádření specifické rychlosti růstu. Pro \(x\) rovno nule je pravá strana rovnice se specifickou rychlostí růstu rovna \(r\). Odpovídá to specifické rychlosti růstu populace, která roste v prostředí z nulové hodnoty. Proto se parametr \(r\) nazývá invazní parametr.

Rovnici je možno přepsat do tvaru

\[ \frac{\mathrm d \frac xK}{\mathrm d(rt)} = \frac {x}{K}\left(1-\frac xK\right) \]

a po zavedení bezrozměrné velikosti populace \(y=\frac xK\) a bezrozměrného času \(\tau = rt\) má rovnice tvar

\[ \frac{\mathrm d y}{\mathrm d\tau} = y(1-y). \]

To znamená, že bez újmy na obecnosti můžeme v logistické rovnici považovat nosnou kapacitu prostředí i inverzní parametr za jednotkové. Přesněji, vhodnou volbou jednotek můžeme docílit toho, že v uvedených jednotkách budou tyto konstanty numericky rovny jedné. Tohoto docílíme tak, že velikost populace se nebude měřit v počtech kusů, ale v násobcích nosné kapacity prostředí. Podobně, jednotka času se upraví tak, aby invazní parametr byl roven jedné. Tedy jednotkou času bude doba, za jak dlouho by populace dorostla do nosné kapacity prostředí, kdyby populace po celou dobu rostla konstantní rychlostí odpovídající rychlosti růstu od nulové hodnoty.

Poznámka (r-stratégové a K-stratégové)

Prostředí, ve kterém se populace nacházejí, je stále vystaveno změnám a výkyvům. To se odráží i na velikosti populace. Různé druhy živočichů se s těmito perturbacemi vyrovnávají různým způsobem. Některé druhy mají takřka stabilní stavy. Například populace albatrosů (Diomedea exulans) na ostrově Gough Island zůstávala téměř konstantní cca 4000 jedinců od roku 1889 přinejmenším do roku 1971 (viz [1] kapitola 5.3). Takové živočišné druhy nazýváme K-stratégy. Živočišné druhy, jejichž strategií je naopak se v příhodné době rychle rozmnožit, nazýváme r-stratégy a při modelování vývoje populace se tento faktor projevuje vysokým koeficientem \(r\). Terminologie r-strategie a K-strategie je připisována MacArthurovi a Wilsonovi, autorům teorie ostrovní biogeografie.

Více o logistické rovnici viz například [3] kapitola 6.8, [15] kapitola 1.1 a [16] str. 182.

Show code cell source Hide code cell source

def exp_rust(t,x,k=1):
    return k*x
def log_rust(t,x,r=1,K=1):
    return r*x*(1-x/K)
def vB_rust(t,x,r=1,Lmax=1):
    return r*(Lmax-x)

meze = [0,10]
pocatecni_podminka = [0.01]
rovnice = [exp_rust, vB_rust, log_rust]

t = np.linspace(*meze,100)
popisky = ["Exponenciální růst","von Bertalanfyho růst","logistický růst"]
data = {
    popisek: 
       solve_ivp(
           r, 
           meze, 
           pocatecni_podminka, 
           t_eval=t).y[0] 
       for popisek,r in zip(popisky,rovnice)}
df = pd.DataFrame(index=t, data = data)

ax = df.plot()
ax.set(
    ylim=(0,1.5),
    title="Tři růstové modely"
    )
ax.grid()
ax.legend();

4.4. Autoregulace a rychlost syntézy proteinů (volitelně)

Tento text je zpracován podle knihy [2] a pojednává o tom, jak zpětná vazba může ovlivnit produkci proteinu. Ukazuje několik strategií, jak může příroda zajistit, že v případě potřeby je protein syntetizován rychle a v dostatečném množství. Zaměříme se na matematickou stránku věci. Pěkná přednáška autora knihy a jednoho ze klíčových vědců v systémové biologii, moderní vědě, která se touto problematikou zajímá, je k dispozici na Youtube zde.

Uvažujme model syntézy proteinu, který degraduje rychlostí \(s(x)=\beta x,\) kde \(\beta\) je konstanta, tj. rychlostí úměrnou množství proteinu \(x\). To je realistický a měřením potvrzený předpoklad. Kromě toho je protein ještě i syntetizován jiným procesem. Při dosažení rovnováhy mezi degradací a produkcí je jeho úroveň konstantní.

Schopnost řízení syntézy správných proteinů ve správnou dobu je klíčová pro všechny organismy. Pro některé jednodušší organismy je vzájemný řetězec na sebe navazujících reakcí do značné míry zmapován a popsán. Tato spleť reakcí je výsledkem dlouhodobé evoluce, kde náhodné genové mutace změnily chod dosud zavedených věcí. Tyto mutace buď přinesly svému nositeli výhodu a udržely se a rozšířily, nebo naopak přinesly nevýhodu a jejich nositel mutaci dále nešířil, protože nebyl tak úspěšný v reprodukci.

V této podkapitole si ukážeme, jak se dá různými strategiemi ovlivnit rychlost, s jakou je v buňce syntetizován protein. Nejedná se o jedinou záležitost, kterou v souvislosti s chemickými reakcemi v buňce studujeme matematickými prostředky. Dalšími problémy jsou například stabilita a robustnost stacionárních stavů. Přístupy jsou jak kvalitativní (může to takto vůbec fungovat?), tak kvantitativní (dostáváme při předpovědích vypočtených z modelů správné numerické hodnoty pro pozorované veličiny?) a v obou přístupech je dovednost modelování pomocí diferenciálních rovnic nezastupitelnou pomůckou.

4.4.1. Produkce konstantní rychlostí

Množství proteinu označme \(x\) a předpokládejme produkci konstantní rychlostí. Spolu s degradací z předchozího odstavce tedy máme model

\[\frac{\mathrm dx}{\mathrm dt}=\alpha - \beta x.\]

4.4.1.1. Nondimenzionalizace

Vhodnou volbou jednotek pro veličinu \(x\) je možné docílit toho, že platí \(\alpha = \beta.\) Opravdu, rovnici je možno přepsat na tvar

\[\frac{\mathrm d x}{\mathrm dt}=\alpha \left(1- \frac{\beta x}{\alpha} \right)\]

a odsud po vynásobení faktorem \(\frac \beta\alpha\)

\[ \frac{\mathrm d\frac{\beta x}{\alpha}}{\mathrm dt}=\beta \left(1 - \frac{\beta x}{\alpha} \right), \]

což v nových jednotkách \(X=\frac {\beta x}\alpha\) vede na rovnici

\[\frac{\mathrm d X}{\mathrm dt}=\beta \left(1 - X \right).\]

Tato volba znamená, že množství proteinu měříme v procentech rovnovážného stavu. Vhodnou volbou jednotky času je možné dosáhnout toho, že společná konstanta \(\beta\) je numericky rovna jedné. Tuto volbu však dělat nebudeme, protože chceme porovnávat časový průběh pro různé hodnoty konstanty \(\beta\). Pro pohodlí se navíc vrátíme k původnímu označení malým písmenem, tj. budeme studovat rovnici

\[ \frac{\mathrm d x}{\mathrm dt}=\beta \left(1 - x \right).\]

Toto je rovnice

\[ \frac{\mathrm d (x-1)}{\mathrm dt}=-\beta \left(x - 1 \right), \]

tj. rovnice popisující rozklad rychlostí úměrnou množství pro veličinu \(x-1\) a řešením je tedy

\[x(t)=1-(1-x_0) e^{-\beta t}. \]

Přestože máme k dispozici analytické řešení, vyřešíme si úlohu numericky, abychom mohli poté volit různé rychlosti produkce.

4.4.1.2. Růstové křivky

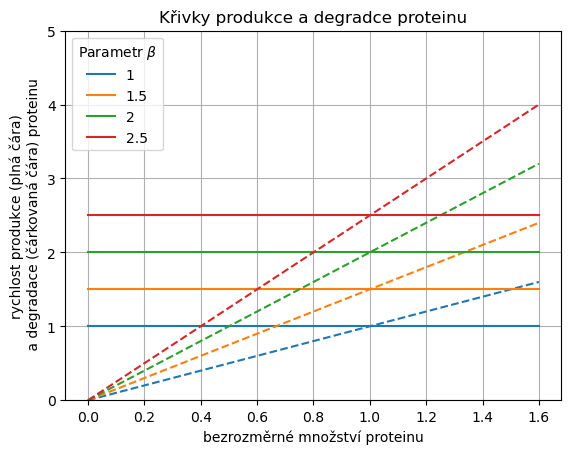
Nejprve nakreslíme křivky produkce a degradace do jednoho obrázku, abychom dokázali lokalizovat stacionární body.

• Křivky pro stejné hodnoty parametru jsou stejnou barvou.

• Průsečík křivek stejné barvy je stacionární bod systému při nastavení parametrů daném příslušnou barvou. Všimněte si, že všechny tyto průsečíky jsou nad sebou a každý v jiné výšce. Pro všechny parametry nastává stacionární stav pro stejné množství proteinu \(x=1\), ale rychlosti produkce a degradace se v tomto stacionárním stavu liší.

• Všechna nastavení parametrů vykazují převažující růst pro malé a převažující degradaci pro velké hodnoty \(x\). Stacionární body jsou tedy stabilní.

Show code cell source Hide code cell source

beta = [1,1.5,2,2.5]              # definice parametrů
x = np.linspace(0, 1.6, 100)  # definice intervalu pro kreslení růstových křivek
fig, ax = plt.subplots()

for i,beta_ in enumerate(beta):       # Cyklus přes parametry
    produkce = beta_+0*x       # Křivka produkce
    degradace = beta_*x        # Křivka degradace
    ax.plot(x,produkce, color="C"+str(i), label=beta_)     # Vykreslení křivky produkce
    ax.plot(x,degradace, "--", color="C"+str(i), label=None)    # Vykreslení křivky degradace

ax.set(title="Křivky produkce a degradce proteinu", 
       xlabel='bezrozměrné množství proteinu',
       ylabel='rychlost produkce (plná čára)\n a degradace (čárkovaná čára) proteinu',
       ylim=(0, 5)
       );
plt.legend(
    title=r"Parametr $\beta$"
    )
plt.grid();

4.4.1.3. Časový vývoj řešení

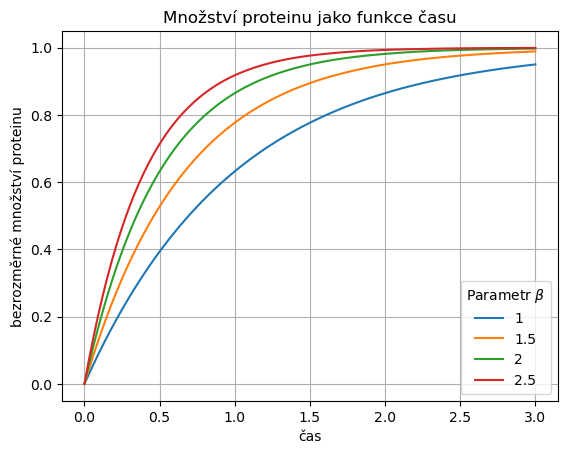
Průběh řešení pro jednotlivé hodnoty parametru u řešení vycházejícího z nulové počáteční podmínky je na obrázku. V praxi nás zajímá, jak rychle bude dosaženo určitého množství proteinu. Tedy vybereme si nějakou hladinu, například \(0.6\), a sledujeme, která křivka této hladiny dosáhne jako první a která jako poslední.

Show code cell source Hide code cell source

meze = [0,3]                # definice počátečního a koncového časového okamžiku
t = np.linspace(*meze, 100) # definice intervalu pro kreslení funkcí času
reseni = np.array([
    solve_ivp(
        lambda t, x: beta_ * (1 - x),
        meze, 
        [0], 
        t_eval=t).y[0]  
    for beta_ in beta
    ]).T

plt.plot(t,reseni)

ax = plt.gca()
ax.set(
    title="Množství proteinu jako funkce času", 
    xlabel='čas', 
    ylabel='bezrozměrné množství proteinu',
    )
plt.grid()
plt.legend(
    beta,
    title=r"Parametr $\beta$"
    );

4.4.1.4. Rychlá produkce je „zaplacena“ rychlou degradací

Je patrné, že nejrychleji hladina enzymu roste pro nejvyšší hodnotu parametru. Vodorovnou čáru ve výšce \(0.6\) protne jako první křivka odpovídající nejvyšší hodnotě parametru \(\beta\). Být první je neskutečně důležité, někdy přímo otázka života a smrti. Taková bakterie, která umí rychle produkovat enzym, například umí rychle uniknout z prostředí s nepříznivými životními podmínkami (rychle sestaví proteiny, které vytvoří jakýsi molekulární motor a ten buňku posune na jiné místo) nebo umí rychle začít ukládat v přítomnosti glukózy energii pro budoucí využití. Na druhou stranu, popsaným mechanismem je rychlost je dosažena nejenom rychlou produkcí, ale i rychlou degradací proteinu. Tedy protein se rychle produkuje a rychle rozpadá. Už z laického hlediska se takový postup nezdá být postupem optimálním pro přežití. Je to jako bychom u auta chtěli mít možnost okamžitě zrychlit a za tímto účelem udržovali vysoké otáčky motoru, ale abychom jeli rozumnou rychlostí tak bychom brzdili. Tedy bychom současně šlapali na plyn i na brzdu. To rozumný člověk nedělá.

Proteiny ve skutečnosti nejsou rychle odbourávány. Popsaný mechanismus šlapání na brzdu a plyn současně v buněčném světě ve skutečnosti není použit. Životnost proteinu není řádově odlišná od životnosti buňky. Příroda a evoluce by takové plýtvání nepřipustily a namísto toho se k problému rychlé produkce proteinu staví jinak. Použitím zpětné vazby, což je předmětem následující kapitoly.

4.4.1.5. Bezrozměrná formulace

Zkusíme ještě přepsat rovnici s konstantní produkcí do bezrozměrných jednotek. Rovnici

\[\frac{\mathrm dx}{\mathrm dt}=\beta(1-x)\]

je možno přepsat do tvaru

\[\frac{\mathrm dx}{\mathrm d(\beta t)}=1-x\]

a pro bezrozměrný čas \(\tau = \beta t\) se rovnice redukuje na

\[\frac{\mathrm dx}{\mathrm d\tau}=1-x.\]

Rovnice je nezávislá na parametrech a po převodu na bezrozměrný čas (tj. po vynásobení času parametrem \(\beta\)) všechna řešení budou splývat. Protože v grafu se budou překrývat, vykreslíme je různě širokými poloprůhlednými čarami.

Show code cell source Hide code cell source

for i,beta_ in enumerate(beta):
    plt.plot(t*beta_,reseni[:,i],label=beta_,lw=(10-2*i),alpha=0.3)
ax = plt.gca()
ax.set(
    xlabel="bezrozměrný čas",
    ylabel="bezrozměrné množství proteinu",
    title="Syntéza proteinu v bezrozměrných jednotkách"
)
plt.legend();

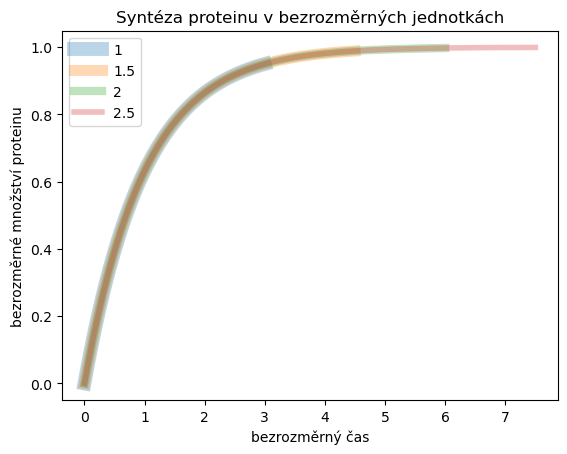
Vidíme názorně výhodu bezrozměrných jednotek. Není nutné řešit rovnici pro různé hodnoty parametru, ale všechna řešení jsou až na transformaci stejná. Jinými slovy vyjádřeno, v modelu

\[\frac{\mathrm dx}{\mathrm dt}=\alpha-\beta x\]

produkce konstantní rychlostí je možno bez újmy na obecnosti položit oba parametry \(\alpha\) a \(\beta\) rovny jedné.

4.4.2. Produkce se zápornou zpětnou vazbou

Předpokládejme produkci proteinu rychlostí související s množstvím proteinu. Jedná se tedy o model

\[\frac{\mathrm dx}{\mathrm dt}=f(x) - \beta x,\]

kde \(f(x)\) je rychlost produkce. Budeme porovnávat vliv funkce \(f(x)\) na rychlost syntézy.

Vhodný tvar funkce \(f(x)\) může být například rozdíl konstanty a třetí mocniny, tj.

\[ f(x)=a-bx^3.\]

Čím vyšší hodnota koeficientu \(\alpha\), tím je počáteční produkce rychlejší a dříve je dosaženo potřebného množství enzymu. Toto se děje při konstantní zpětné vazbě a konstantním stacionárním stavu (všechny rovnice mají člen popisující degradaci ve tvaru \(-x\) a stacionární stav \(x=1\)).

4.4.2.1. Nondimenzionalizace

Vhodnou volbou jednotek pro veličinu \(x\) dosáhneme toho, že stacionárním bodem bude \(x=1\) (jinými slovy, množství enzymu budeme měřit v procentech rovnovážného stavu). Protože budeme uvažovat stále stejnou rychlost degradace a sledovat jenom vliv funkce \(f(x)\), můžeme jednotky času zvolit tak, že \(\beta = 1\). Tj. studujeme rovnici

\[\frac{\mathrm dx}{\mathrm dt}=f(x) - x,\]

kde \(f(1)=1\). Aby byla navíc splněna podmínka \(f(1)=1\), budeme uvažovat funkci

\[f(x)=\alpha-(\alpha-1)x^3, \quad \alpha \geq 1.\]

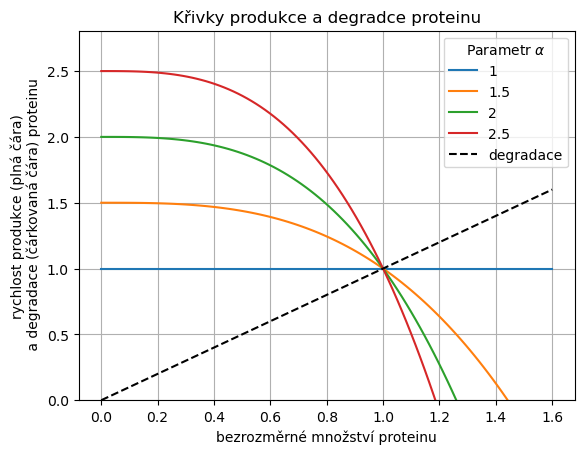
4.4.2.2. Křivky růstu a degradace

Funkce

\[f(x)=\alpha-(\alpha-1)x^3, \quad \alpha \geq 1\]

je klesající funkce. Rychlost produkce tedy ubývá s množstvím. Toto se nazývá záporná zpětná vazba. Parametr \(\alpha\) reguluje sílu této zpětné vazby, čím je vyšší, tím je zpětná vazba výraznější. Vyšší \(\alpha\) charakterizuje vyšší hodnotu průsečíku na svislé ose (rychlejší produkci při nulové hladině proteinu) a rychlejší pokles při rostoucí koncentraci. Pěkně to je vidět na následujícím obrázku.

Show code cell source Hide code cell source

alpha = [1,1.5,2,2.5]              # definice parametrů
x = np.linspace(0, 1.6, 100)  # definice intervalu pro kreslení růstových křivek
fig, ax = plt.subplots()

for i,alpha_ in enumerate(alpha):       # Cyklus přes parametry
    produkce = alpha_ - (alpha_-1)*x**3 # Křivka produkce
    ax.plot(x,produkce, color="C"+str(i), label=alpha_)     # Vykreslení křivky produkce

ax.plot(x,x, "--", color="k", label="degradace")    # Vykreslení křivky degradace

ax.set(title="Křivky produkce a degradce proteinu", 
       xlabel='bezrozměrné množství proteinu',
       ylabel='rychlost produkce (plná čára)\n a degradace (čárkovaná čára) proteinu',
       ylim=(0, None)
       );
plt.legend(
    title=r"Parametr $\alpha$"
    )
plt.grid();

4.4.2.3. Časový průběh řešení modelu

Zkusíme si namodelovat průběh řešení modelu pro různé hodnoty parametru.

Show code cell source Hide code cell source

meze = [0,3]                # definice počátečního a koncového časového okamžiku
t = np.linspace(*meze, 100) # definice intervalu pro kreslení funkcí času
reseni = np.array([
    solve_ivp(
        lambda t, x: alpha_ - (alpha_-1)*x**3 - x,
        meze, 
        [0], 
        t_eval=t).y[0]  
    for alpha_ in alpha
    ]).T

plt.plot(t,reseni)

ax = plt.gca()
ax.set(
    title="Množství proteinu jako funkce času", 
    xlabel='čas', 
    ylabel='bezrozměrné množství proteinu',
    )
plt.grid()
plt.legend(
    alpha,
    title=r"Parametr $\alpha$"
    );

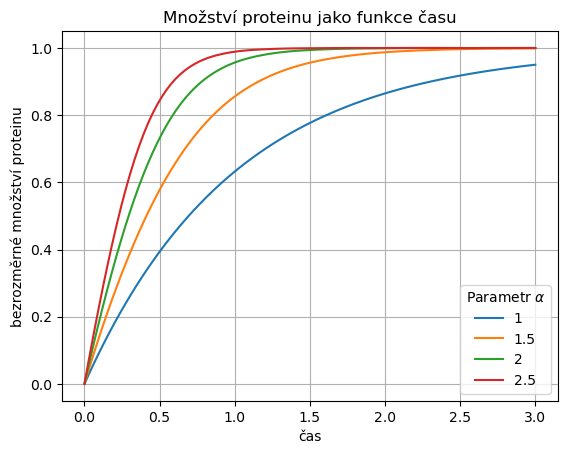
Čím vyšší hodnota koeficientu \(\alpha\), tím je počáteční produkce rychlejší a dříve je dosaženo potřebného množství enzymu. Toto se děje při konstantní zpětné vazbě a konstantním stacionárním stavu (všechny rovnice mají člen popisující degradaci ve tvaru \(-x\) a stacionární stav \(x=1\)).

4.4.2.4. Negativní zpětná vazba urychluje syntézu

Vidíme, že negativní zpětná vazba příznivě ovlivňuje rychlost syntézy proteinu. Tím je buňce umožněno zareagovat rychle na vnější podmínky, aniž by za to platila cenou rychlé degradace, jako bez zpětné vazby (současně přidávání plynu a brzdění). Taková zpětná vazba může být zprostředkována například tím, že protein vstupuje do jiných chemických reakcí.

Příroda zařadila i do jednoduchých organismů typu buňka takových zpětných vazeb obrovské množství a dlouholetou evolucí vyladila hodnoty parametrů tak, aby potřebné proteiny vznikaly přesně v době, kdy jsou potřeba a aby dostatečně rychle vznikly v potřebné koncentraci. To je zařízeno mutacemi v genech. Chybou v přepise genů například může vzniknout zpětná vazba, která do té doby neexistovala. Pokud se projeví jako užitečná, dává svému nositeli evoluční výhodu a šíří se dál. Podobně se během milionů let vyladí parametry této zpětné vazby, například hodnota parametru \(\alpha\). Těmito problémy zabývá věda nazývaná systémová biologie. Tato věda prodělala bouřlivý rozvoj v letech okolo roku 2000, kdy byly vyvinuty účinné postupy pro získávání potřebných dat o genech a proteinech a tento rozvoj pokračuje dodnes.

Poznatky, na kterých je založen tento model, jsou potvrzeny experimentálně. Používá se například vnesení genu způsobujícího světélkování do genetické informace bakterií.