4. Lov v populaci - časový vývoj

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

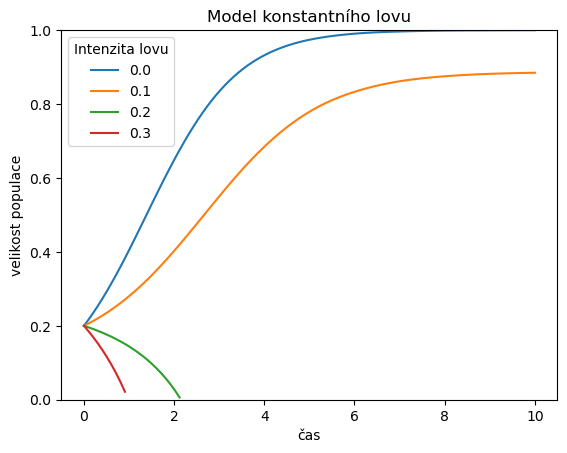
4.1. Konstantní lov

### Příprava funkcí a parametrů
pocatecni_podminka = [0.2]  # počáteční podmínka
meze = np.array([0,10]) # interval, na kterém hledáme řešení
parametry = [0,0.1,0.2,0.3] # seznam parametrů
n = 100

def rovnice(t, x, r=1, K=1, h=0.15):
    if x<0:
        return np.nan  # pro zaporne hodnoty vraceme nedefinovany vyraz, zaporne velikosti populaci nemaji smysl
    return r*x*(1-x/K)-h


### Řešení modelu
t=np.linspace(*meze, n)  # definiční obor, v těchto bodech budeme hledat řešení
df = pd.DataFrame(index=t)      # tabulka pro výstup
df.index.name = "čas"

for parametr in parametry:
    reseni = solve_ivp(
                       lambda t,x:rovnice(t,x,h=parametr),
                       meze,
                       pocatecni_podminka,
                       t_eval=t
                       )
    df.loc[reseni.t,parametr] = reseni.y.T # další sloupec tabulky
    # lambda funkce viz https://www.w3schools.com/python/python_lambda.asp
    # (dočasná nepojmenovaná funkce)

### Vizualizace řešení
ax = df.plot()
ax.set(
    ylim = (0,1),
    title = "Model konstantního lovu",
    ylabel="velikost populace",
)
plt.legend(title="Intenzita lovu")

<matplotlib.legend.Legend at 0x7f11ef999a60>

df

	0.0	0.1	0.2	0.3
čas
0.00000	0.200000	0.200000	0.200000	0.200000
0.10101	0.216652	0.206247	0.195834	0.185414
0.20202	0.234284	0.212874	0.191401	0.169871
0.30303	0.252886	0.219894	0.186676	0.153255
0.40404	0.272441	0.227323	0.181642	0.135432
...	...	...	...	...
9.59596	0.999672	0.883707	NaN	NaN
9.69697	0.999703	0.883959	NaN	NaN
9.79798	0.999732	0.884196	NaN	NaN
9.89899	0.999757	0.884421	NaN	NaN
10.00000	0.999780	0.884635	NaN	NaN

100 rows × 4 columns

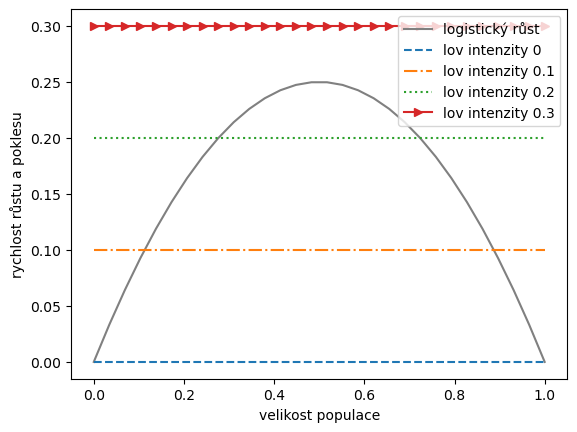
params = {'style':["-","--","-.",":",">-"], 'color':['gray','C0','C1','C2','C3']}
x = np.linspace(0,1,30)
df = pd.DataFrame(index = x)
df.index.name = "velikost populace"
r,K = 1,1
df["logistický růst"] = r*x*(1-x/K)
for h in parametry:
    df[f"lov intenzity {h}"] = 0*x + h
ax = df.plot(**params)
plt.legend(loc='upper right')
ax.set(ylabel="rychlost růstu a poklesu")
# plt.grid()

[Text(0, 0.5, 'rychlost růstu a poklesu')]

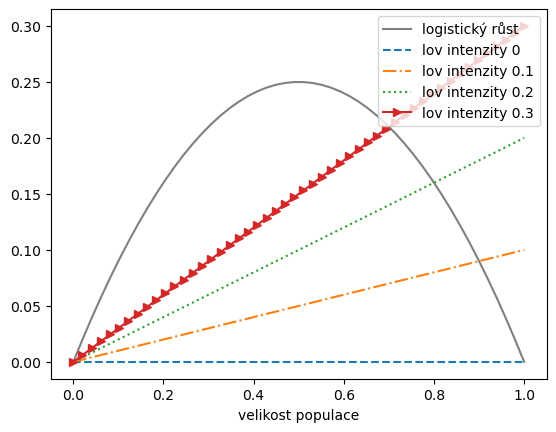
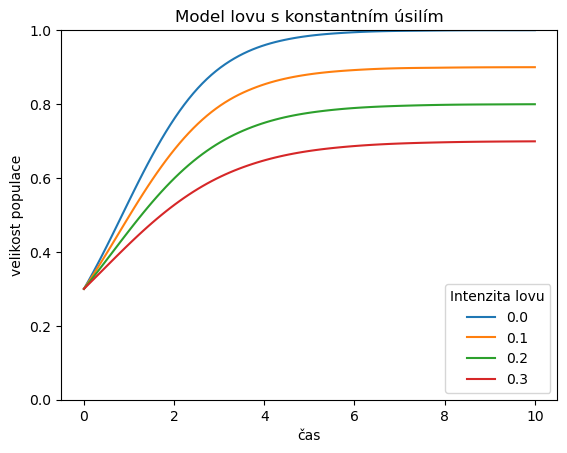
4.2. Lov konstantním úsilím

x = np.linspace(0,1)
df = pd.DataFrame(index = x)
df.index.name = "velikost populace"
r,K = 1,1
df["logistický růst"] = r*x*(1-x/K)
for h in parametry:
    df[f"lov intenzity {h}"] = x * h
df.plot(**params)
plt.legend(loc='upper right')

<matplotlib.legend.Legend at 0x7f11ef1de4e0>

### Příprava funkcí a parametrů
pocatecni_podminka = np.array([0.3])  # počáteční podmínka
meze = np.array([0,10]) # interval, na kterém hledáme řešení
parametry = [0,0.1,0.2,0.3] # seznam parametrů
n = 100

def rovnice(t, x, r=1, K=1, h=0.15):
    return r*x*(1-x/K)-h*x


### Řešení modelu
t=np.linspace(*meze, n)  # definiční obor, v těchto bodech budeme hledat řešení
df = pd.DataFrame()      # tabulka pro výstup
df.index = t              # sloupec s časem

for parametr in parametry:
    reseni = solve_ivp(
                       lambda t,x:rovnice(t,x,h=parametr),
                       meze,
                       pocatecni_podminka,
                       t_eval=t
                       )
    df[parametr] = reseni.y.T # další sloupec tabulky
    # lambda funkce viz https://www.w3schools.com/python/python_lambda.asp
    # (dočasná nepojmenovaná funkce)

### Vizualizace řešení
ax = df.plot()
ax.set(
    ylim = (0,1),
    title = "Model lovu s konstantním úsilím",
    xlabel="čas",
    ylabel="velikost populace",
)
plt.legend(title="Intenzita lovu")

<matplotlib.legend.Legend at 0x7f11edc3e4e0>

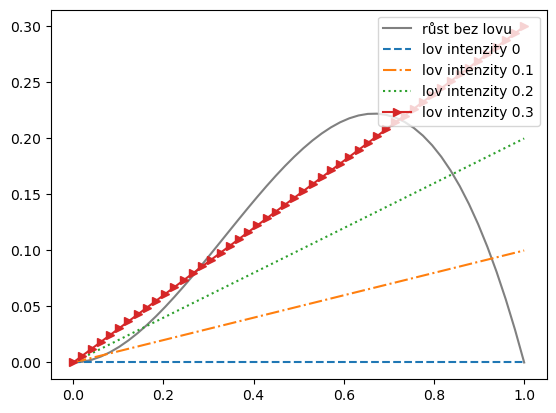
4.3. Lov populace se slabým a silným Aleeho efektem

x = np.linspace(0,1)
df = pd.DataFrame(index = x)
r,K = 1,1
df["růst bez lovu"] = r*x**2*(1-x/K)*1.5
for h in parametry:
    df[f"lov intenzity {h}"] = x * h
df.plot(**params)
plt.legend(loc='upper right')

<matplotlib.legend.Legend at 0x7f11e5ac2150>

x = np.linspace(0,1)
df = pd.DataFrame(index = x)
r,K = 1,1
df["růst bez lovu"] = r*x*(1-x/K)*(x/.2-1)/2
for h in parametry:
    df[f"lov intenzity {h}"] = x * h
df.plot(**params)
plt.legend(loc='upper right')

<matplotlib.legend.Legend at 0x7f11e56bec30>