11. Diskrétní populační modely

Diskrétní populační modely jsou zpravidla rekurentní vzorce, které určují velikost populace nebo populací v dalším roce na základě velikostí v předchozím roce (modely prvního řádu) nebo několika předchozích let (modely vyššího řádu). Je-li závislost lineární, můžeme tyto modely zapsat pomocí maticového násobení, jak jsme poznali již dříve například u Leslieho matice. To je výhodné, protože můžeme využít rozvinutý aparát lineární algebry.

Výhodou diskrétních maticových modelů oproti spojitým je jednodušší řešení. To spočívá v opakovaném používání modelu a v postupném výpočtu populačních stavů jenom použitím jednoduchých matematických operací. Nevýhodou je horší možnost nalezení analytického řešení a že se modely někdy mohou chovat nečekaně, viz například chaos v diskrétní logistické rovnici.

11.1. Diskrétní modely jednodruhové populace

11.1.1. Základní diskrétní modely

Diskrétní model jednodruhové populace modelovaný rovnicí prvního řádu má obecný tvar

\[x(k+1)=x(k) f(x(k)),\]

kde funkce \(f\) charakterizuje působení vnitrodruhové konkurence.

Základní diskrétní model, diskrétní logistickou rovnici, jsme poznali dříve. Tento model je jednoduchý, ale má komplikované chování, které může vést k periodickým řešením s vysokou periodou a k chaosu.

Ukážeme si volbu tří funkcí, které mají společné chování v počátku a při dosažení nosné kapacity prostředí. Konkrétně, platí \(f(0)=r\) a \(f(K)=1\).

• Logistický růst

  \[x(k+1)=r x(k)\left(1-\frac{x(k)}{K}\frac{r-1}{r}\right)\]

• Bevertonova–Holtova rovnice, logistická rovnice Pielou:

  \[x(k+1)=x(t)\frac{rK}{K+(r-1)x(k)}\]

• Rickerova logistická rovnice:

  \[ x(k+1)=x(k)e^{\left(1-\frac {x(t)}K\right)\ln r} \]

Show code cell source Hide code cell source

import numpy as np  # knihovna pro numerické výpočty
import matplotlib.pyplot as plt  # knihovna pro grafiku
import pandas as pd # knihovna pro praci s tabulkami

Show code cell source Hide code cell source

N = 70
x_p = np.zeros(N)
x_p[0] = 5
x_r = x_p.copy()
x_l = x_p.copy()
r = 1.2
K = 100

for k in range(N-1):
    x_p[k+1] = x_p[k]*(r*K)/(K+(r-1)*x_p[k])
    x_r[k+1] = x_r[k]*np.exp((1-x_r[k]/K)*np.log(r))
    x_l[k+1] = x_l[k]*r*(1-x_l[k]/(K*r/(r-1)))

fig, ax = plt.subplots()
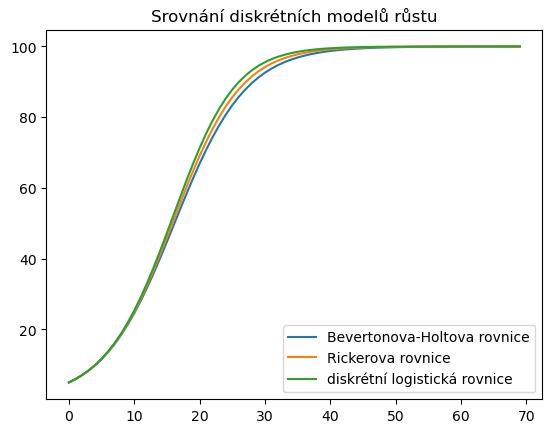
ax.plot(x_p, label = "Bevertonova-Holtova rovnice")
ax.plot(x_r, label = "Rickerova rovnice")
ax.plot(x_l, label = "diskrétní logistická rovnice")
ax.legend()
ax.set(
    title="Srovnání diskrétních modelů růstu");  

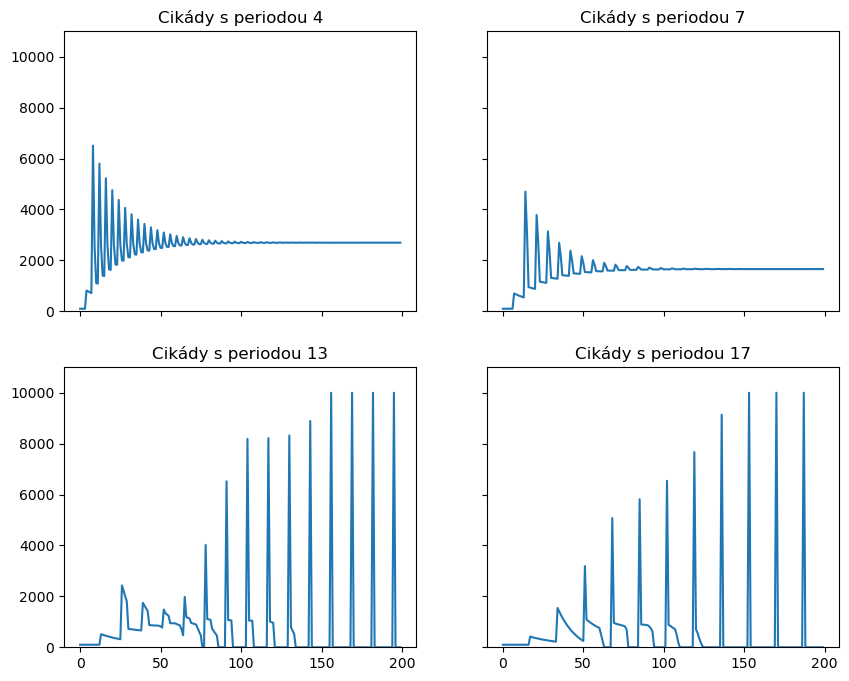
11.1.2. Periodické cikády

Periodické cikády

Cikády Magicicada septendecim se vyznačují synchronizovaným výskytem jednou za 17 let. Celou dobu čekají jako larvy v zemi, aby se po 17 letech vylíhly a nakladly vajíčka pro další generaci.

V roce 2007 byl v Cincinnati teplý leden, ale v únoru byla opět zima. V tomto roce měly stromy dvě sady listí. To způsobilo, že cikády se vylíhly o rok dříve, po 16 letech. Viz Kevin Fitzgerald: How Do Cicadas Know When to Emerge from the Ground? (leden 2023).

Obrázek: https://www.flickr.com/photos/lalo_pangue/8931871182

Následující model je zpracován podle [14] a vysvětluje zajímavý efekt vyskytující se v životě cikád Magicicada septendecim, M. cassini a M. septendecula.

Dospělé cikády během pár týdnů svého života nakladou vajíčka u stromů, kde se vylíhly. Z vajíček se vyklubou larvy, které se zavrtají pod zem ke kořenům. Životní cyklus cikád se liší od 3 do 4, 7, 13 nebo 17 let. Poslední dva typy cikád se vyznačují (na východním pobřeží severní Ameriky) masovým synchronizovaným výskytem. Viz například následující video.

Předpokládejme, že druh má životní cyklus \(k\) let, larvy dospějí a objeví se na povrchu \(k\) let po smrti rodičů. Nechť \(n_t\) je počet larev, které se v roce \(t\) zavrtají do země, najdou útočiště a potravu u kořenů stromů a za \(k\) let se z nich (pokud přežijí) vylíhnou dospělé cikády.

Předpokládejme, jenom zlomek \(\mu\) larev přežije do každého dalšího roku. V roce \(t\) se vylíhnou larvy, které se před \(k\) lety zavrtaly do země (jejich počet byl \(n_{t-k}\)) a v zemi přežily celkem \(k\) let (každý rok jich přežije jenom \(\mu\)-násobek a proto \(k\) let přežije \(\mu^kn_{t-k}\) larev). Tyto larvy se objeví v roce \(t\) jako dospělí, kteří uzavřou cyklus. Z tohoto počtu predátoři zlikvidují \(p_t\) cikád a pro další rozmnožování zůstane \([\mu^kn_{t-k}-p_t]_+\) jedinců, kde \([x]_+=\max(x,0)\). Jestliže se každé cikádě narodí průměrně \(f\) larev, přibude v tomto roce

\[M_t=f\cdot[\mu^kn_{t-k}-p_t]_+\]

larev.

Je-li \(D\) celková nosná kapacita prostředí, je volná kapacita dána vztahem

\[c_t=\left[D-\sum_{i=1}^{k-1}\mu^in_{t-i}\right]_+,\]

protože část této kapacity obsadily larvy z loni, předloni, předpředloni atd. Z \(M_t\) narozených larev se maximálně \(c_t\) může zavrtat do země a přežít. Proto počet larev v dalším roce dán vztahem \(n_t=\min\left(M_t, c_t\right)\).

Působení predátorů (živí se dospělými cikádami) můžeme modelovat rovnicí

\[p_t=\nu p_{t-1}+a\mu^kn_{t-k-1},\]

kde \(\nu<1\) (bez cikád predátoři vymírají, toto vymírání se zastavuje s počtem cikád, které se loni vylíhly).

Pro lepší formulaci numerického modelu posuneme index \(t\) o jedničku.

\[ \begin{aligned} p_{t+1}&=\nu p_t+a\mu^kn_{t-k} \\ c_{t+1}&=\Bigl[D-\sum_{i=1}^{k-1}\mu^in_{t+1-i}\Bigr]_+\\ M_{t+1}&=f\cdot\bigl[\mu^k n_{t+1-k}-p_{t+1}\bigr]_+ \\ n_{t+1}&=\min(M_{t+1}, c_{t+1}) \end{aligned} \]

Show code cell source Hide code cell source

def cikady(
    a=.042, # parametry populace (Murray)
    f=10,
    D=10000,
    nu=.95,
    mu=.95,
    k=4, # perioda cikad
    N = 200, # delka simulace
    n0 = 100 # pocatecni hodnoty
    ):

    n = np.zeros(N)
    p = np.zeros(N)
    n[0:k] = n0

    for t in range(k-1,N-1):
        p[t+1] = nu*p[t] + a*mu**k*n[t-k]
        c = max(
              0,
              D-sum([mu**(i)*n[t+1-i] for i in range(1,k)])
              )
        M = max(
              0,
              f*(mu**k*n[t+1-k]-p[t+1])
              )
        n[t+1] = min(M,c)
    return n

stadium_larvy = [4,7,13,17]
reseni = np.array([cikady(k=k) for k in stadium_larvy])
reseni = pd.DataFrame(reseni.T,columns = stadium_larvy)
reseni.tail(20).T.style.background_gradient(axis=1).format(precision=0)

	180	181	182	183	184	185	186	187	188	189	190	191	192	193	194	195	196	197	198	199
4	2696	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695
7	1657	1657	1658	1658	1657	1657	1657	1657	1657	1658	1658	1657	1657	1657	1657	1657	1658	1658	1657	1657
13	0	0	10000	0	0	0	0	0	0	0	0	0	0	0	0	10000	0	0	0	0
17	0	0	0	0	0	0	0	10000	0	0	0	0	0	0	0	0	0	0	0	0

Varianta použitelná pro velké tabulky, podle User Guide.

Show code cell source Hide code cell source

def magnify():
    return [dict(selector="th",
                 props=[("font-size", "4pt")]),
            dict(selector="td",
                 props=[('padding', "0em 0em")]),
            dict(selector="th:hover",
                 props=[("font-size", "12pt")]),
            dict(selector="tr:hover td:hover",
                 props=[('max-width', '200px'),
                        ('font-size', '12pt')])
]

reseni.tail(50).T.style.background_gradient(axis=1)\
    .set_properties(**{'max-width': '80px', 'font-size': '2pt'})\
    .set_caption("Hover to magnify")\
    .format(precision=0)\
    .set_table_styles(magnify())

Hover to magnify

	150	151	152	153	154	155	156	157	158	159	160	161	162	163	164	165	166	167	168	169	170	171	172	173	174	175	176	177	178	179	180	181	182	183	184	185	186	187	188	189	190	191	192	193	194	195	196	197	198	199
4	2694	2694	2698	2695	2695	2695	2697	2695	2695	2695	2697	2695	2695	2695	2697	2695	2695	2695	2697	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695	2696	2695	2695	2695
7	1657	1657	1657	1657	1660	1659	1657	1657	1657	1657	1657	1659	1658	1657	1657	1657	1657	1657	1659	1658	1657	1657	1657	1657	1657	1658	1658	1657	1657	1657	1657	1657	1658	1658	1657	1657	1657	1657	1657	1658	1658	1657	1657	1657	1657	1657	1658	1658	1657	1657
13	0	0	0	0	0	0	10000	0	0	0	0	0	0	0	0	0	0	0	0	10000	0	0	0	0	0	0	0	0	0	0	0	0	10000	0	0	0	0	0	0	0	0	0	0	0	0	10000	0	0	0	0
17	0	0	0	10000	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	10000	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	10000	0	0	0	0	0	0	0	0	0	0	0	0

Grafické znázornění.

Show code cell source Hide code cell source

fig, axs = plt.subplots(
                      2,
                      2,
                      figsize=(10,8), 
                      sharex=True, 
                      sharey=True
                      )
D = 10000
for k,ax in zip([4, 7, 13, 17], axs.flatten()):
    ax.plot(reseni[k])
    ax.set(
      ylim=(0,D*1.1),
      title="Cikády s periodou "+str(k))

11.2. Diskrétní modely dvou populací