6. Model konkurence

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

Následující kód modeluje chování společenství konkurence dvou populací pomocí soustavy rovnic

\[\begin{split} \begin{aligned} \frac{\mathrm dx}{\mathrm dt}={}&(a-bx-cy)x,\\ \frac{\mathrm dy}{\mathrm dt}={}&(\alpha-\beta x-\gamma y)y. \end{aligned} \end{split}\]

Koeficienty mezidruhové konkurence \(c\) a \(\beta\) jsou nastaveny tak, aby druh \(x\) dominoval. Ostatní koeficiety jsou nastaveny na jednotkovou velikost. Pro srovnání je studován i model, kdy se populace \(x\) a \(y\) neovlivňují a koeficienty mezidruhové konkurence jsou nulové.

def konkurence(t,X,a=1,b=1,c=0,alpha=1,beta=0,gamma=1):
    x,y= X
    return [(a-b*x-c*y)*x, (alpha-beta*x-gamma*y)*y]

meze = [0,50]
pocatecni_podminka = [0.1,0.5]
t = np.linspace(*meze,500)

df = pd.DataFrame(index=t)
df.index.name ="čas"

for c,beta,sloupce in zip( [0.8,0] , [1.2, 0] , [["x","y"],["x0","y0"]]):
    print (f"Řeším pro c={c}, beta={beta}, výstup do {sloupce}.")
    df[sloupce] = solve_ivp(
                       lambda t,X:konkurence(t,X,c=c,beta=beta),
                       meze,
                       pocatecni_podminka,
                       t_eval=t
                       ).y.T
df.tail()

Řeším pro c=0.8, beta=1.2, výstup do ['x', 'y'].
Řeším pro c=0, beta=0, výstup do ['x0', 'y0'].

	x	y	x0	y0
čas
49.599198	0.999500	0.000271	0.999168	0.999933
49.699399	0.999525	0.000266	0.999247	0.999939
49.799599	0.999548	0.000260	0.999319	0.999945
49.899800	0.999570	0.000255	0.999384	0.999950
50.000000	0.999591	0.000250	0.999442	0.999955

ax = df.plot(
    subplots=[("x","x0"),("y","y0")],
    legend=False,
    style=["-"]*2+["--"]*2
)
ax[0].set(
    ylabel="Druh $x$",
)
ax[1].set(
    xlabel="Čas",
    ylabel="Druh $y$",
)

ax[0].legend(["S konkurencí", "Samostatně"])
ax[1].legend(["S konkurencí", "Samostatně"])
plt.suptitle("Model dvou populací s konkurencí a bez konkurence")
plt.tight_layout();

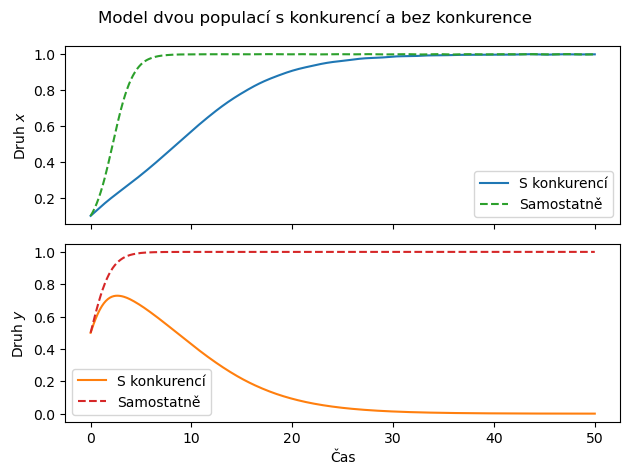
Následující kód je minimalistickým kódem pro model konkurence dvou populací a vykreslení řešení tohoto modelu.

def model(t,X,a=1,b=1,c=0.7,alpha=1,beta=1.2,gamma=1):
    x,y = X
    return [(a-b*x-c*y)*x, (alpha-beta*x-gamma*y)*y]

meze = [0,50]
pocatecni_podminka = [0.1,0.5]
sloupce = ["populace x","populace y"]

t = np.linspace(*meze,500)
df = pd.DataFrame(index=t)
df.index.name ="čas"

df[sloupce] = solve_ivp(
                       model,
                       meze,
                       pocatecni_podminka,
                       t_eval=t
                       ).y.T
ax = df.plot()

ax.set(title="Model dvou populací s konkurencí")
plt.tight_layout();

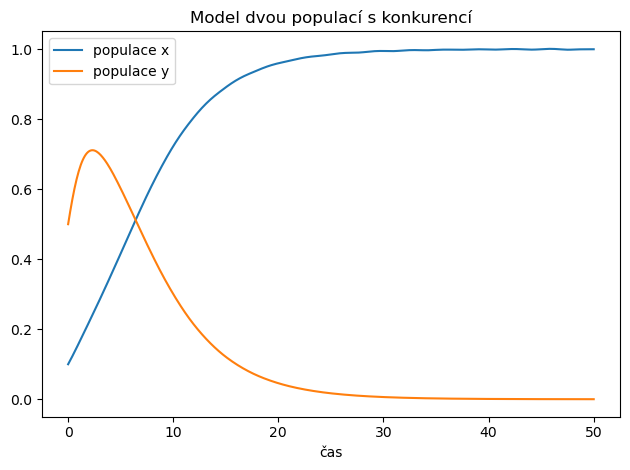
Model upravíme

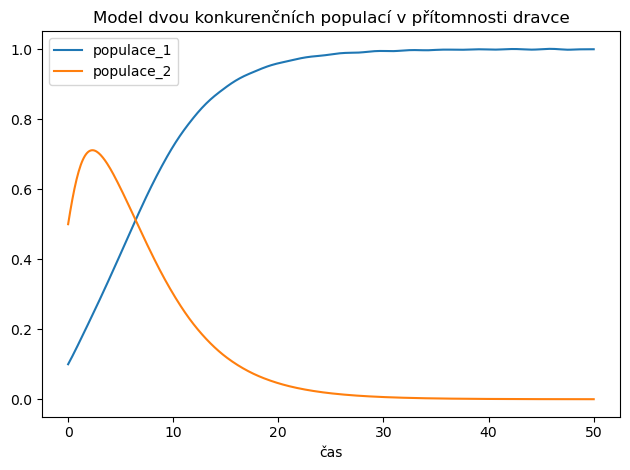
• přidejte do modelu predátora

• predátor se živí dominantní kořistí

• ukažte, že přítomnost predátora může pomoct populaci konkurečně slabšího druhu přežít

• model bude mít

  • tři závislé proměnné,

  • tři rovnice,

  • tři počáteční podmínky,

  • tři sloupce v tabulce s výsledky

def model(t,X,a=1,b=1,c=0.7,alpha=1,beta=1.2,gamma=1):
    x,y = X
    return [(a-b*x-c*y)*x, (alpha-beta*x-gamma*y)*y]

meze = [0,50]
pocatecni_podminka = [0.1,0.5]
sloupce = ["populace_1","populace_2"]

t = np.linspace(*meze,500)
df = pd.DataFrame(index=t)
df.index.name ="čas"

df[sloupce] = solve_ivp(
                       model,
                       meze,
                       pocatecni_podminka,
                       t_eval=t
                       ).y.T
ax = df.plot()

ax.set(title="Model dvou konkurenčních populací v přítomnosti dravce")
plt.tight_layout();

df.tail()

	populace_1	populace_2
čas
49.599198	0.999606	0.000124
49.699399	0.999608	0.000121
49.799599	0.999613	0.000119
49.899800	0.999625	0.000117
50.000000	0.999646	0.000114