Ctrl+K

Modely dravce a kořisti

11. Modely dravce a kořisti#

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

11.1. Lotkův a Volterrův model dravce a kořisti#

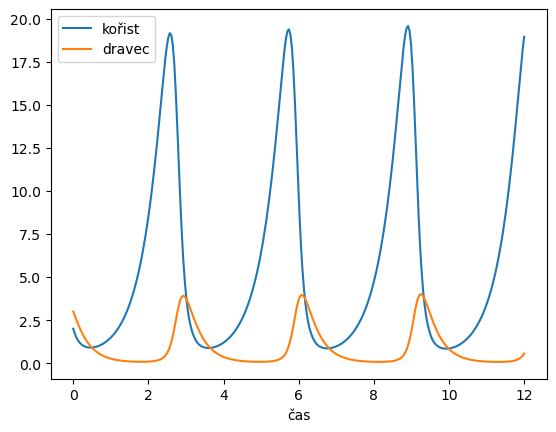
Nakreslete řešení Lotkova a Volterrova modelu dravce a kořisti.

Pokud pro nějaké nastavení parametrů není přehledné kreslit křivky pro kořist obě do jednoho grafu, můžeme každou křivku nakreslit do samostatného grafu. Modifikujte následující kód a použijte pro kreslení parametry příkazu subplots, viz ukázka. Výsledkem nechť je dvojice grafů, v jednom nechť je graf vývoje populace dravce, ve druhém graf vývoje populace kořisti. Časová osa nechť je sdílená pro oba grafy.

## Prostor pro řešení

def prey(x,y,a=1,b=1):
    return a*x - b*x*y

def predator(x,y,c=1,d=0.5):
    return -c*y+d*x*y

def model(t,X,a=1,b=1,c=1,d=0.5):
    x,y = X
    return [prey(x,y,a,b),predator(x,y,c,d)]

meze = [0,12]
pocatecni_podminka = [2,3]
xmax = 6
ymax = 3

fig,ax = plt.subplots()

t = np.linspace(*meze, 300)
sol = solve_ivp(
    lambda t,X:model(t,X, a=2, b=2, c=3, d=.5), 
    meze, # interval pro reseni
    pocatecni_podminka, # pocatecni podminka
    t_eval=t
)

ax.plot(t, sol.y.T)

ax.set(xlabel = 'čas')
ax.legend(['kořist', 'dravec'])
plt.show()
../_images/4ccdff1c6b1ac17c63fd1747debb18053989d32d808b1b38bb6ca8bfc62a2341.png

Modifikujte předchozí kód tak, aby byla populace dravce i kořisti ve stejném obrázku, ale každá funkce měla svou svislou osu. Ukázka této techniky a využití příkazu twinx je v přednášce s numerickou derivací.

## Prostor pro řešení

Pokuste se obrázky doplnit tak, aby z nich bylo zřejmé, jestli perioda řešení souvisí či nesouvisí s počáteční podmínkou. Nakreslete do stejného obrázku řešení s další počáteční podmínkou.

11.2. Model dravce a kořisti s Hollingovou trofickou funkcí#

Zopakujte předchozí kroky pro Rosenzweigův a MacArthurův model s Hollingovou trofickou funkcí.

def predator(x,y):
    return -0.04*y + .1*x*y/(4+x)

def prey(x,y):
    return (1-x/10)*x-.3*x*y/(4+x)

def model(t,X):
    x,y = X
    return [prey(x,y),predator(x,y)]

meze = [0,100]
pocatecni_podminka = [2,12]
xmax = 10
ymax = 20

## atd .... Prostor pro řešení

11.3. Model dravce a dvou populací kořisti#

Pokuste se namodelovat následující situaci.

  • V ekosystému dochází ke konkurenci dvou populací a jedna z populací je konkurencí vyloučena.

  • Přítomnost predátora redukuje velikosti obou populací tak, že se dominance silnější populace neprojeví. Tím predátor zprostředkovává přežití populace, která mu současně slouží jako kořist. Odstranění predátora z ekosystému by paradoxně způsobilo vymření jeho kořisti.

  • Snažte se o co nejjednodušší model. Například modifikujte model z přednášky pro konkurenci tří populací tak, aby třetí populace nebyla konkurentem, ale predátorem.

## Prostor pro řešení
Obsah