Diferenciální rovnice 2

5. Diferenciální rovnice 2#

5.1. Exponenciální růst#

Namodelujeme exponenciální růst

\[\frac{\mathrm dx}{\mathrm dt}=kx\]
pro tři různé parametry \(k\). Protože po transformaci do bezrozměrného času \(\tau = kt\) má rovnice tvar
\[\frac{\mathrm dx}{\mathrm d\tau }=x\]
nezávislý na \(k\), ověříme, že všechna řešení po transformaci do bezrozměrného času splývají.

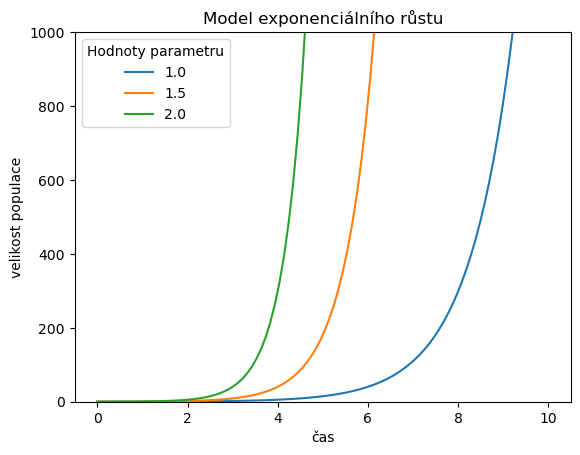
Nejprve růst pro tři různé hodnoty koeficientu \(k\). Vidíme, že čím vyšší je \(k\), tím rychleji velikost populace roste v čase.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

### Příprava funkcí a parametrů
pocatecni_podminka = np.array([0.1])  # počáteční podmínka
meze = np.array([0,10]) # interval, na kterém hledáme řešení
parametry = [1,1.5,2] # seznam parametrů
n = 100
def rovnice(t, x, k=1):
    return k*x

### Řešení modelu
t=np.linspace(*meze, n)  # definiční obor, v těchto bodech budeme hledat řešení
df = pd.DataFrame()      # tabulka pro výstup
df.index = t              # sloupec s časem

for parametr in parametry:
    reseni = solve_ivp(
                       lambda t,x:rovnice(t,x,k=parametr),
                       meze,
                       pocatecni_podminka,
                       t_eval=t
                       )
    df[parametr] = reseni.y.T # další sloupec tabulky
    # lambda funkce viz https://www.w3schools.com/python/python_lambda.asp
    # (dočasná nepojmenovaná funkce)
df
1.0 1.5 2.0
0.00000 0.100000 0.100000 1.000000e-01
0.10101 0.110629 0.116360 1.223884e-01
0.20202 0.122390 0.135402 1.497941e-01
0.30303 0.135402 0.157551 1.833156e-01
0.40404 0.149792 0.183314 2.243435e-01
... ... ... ...
9.59596 1469.825225 178046.326900 2.159632e+07
9.69697 1626.028660 207190.044520 2.643182e+07
9.79798 1798.852275 241143.463018 3.234832e+07
9.89899 1990.068781 280661.211823 3.958971e+07
10.00000 2201.608767 326591.822323 4.845406e+07

100 rows × 3 columns

### Vizualizace řešení
ax = df.plot()
ax.set(
    ylim = (0,1000),
    title = "Model exponenciálního růstu",
    xlabel="čas",
    ylabel="velikost populace",
)
plt.legend(title="Hodnoty parametru")

<matplotlib.legend.Legend at 0x7fbada5d2210>
../_images/6b1280c03c7c7bc995bb0d5b45bd1c7c8bae36026443ca0259051c156bd02a2a.png

5.1.1. Volitelná část#

Po transformaci do bezrozměrného času by měly křivky splynout. Abychom to viděli graficky, budeme postupně snižovat jejich tloušťku a nastavíme částečnou průhlednost. To zajistíme volbami lw (zkratka za linewidth) a alpha.

for k,lw in zip(parametry,[8,5,2]):
    plt.plot(t*k,df[k],lw=lw,label=k,alpha=0.5)  # Na vodorovne ose neni cas ale bezrozmerny cas
ax = plt.gca()
ax.set(
    ylim=(0,100),
    xlim=(0,10),
    xlabel="bezrozměrný čas",
    ylabel="velikost populace",
    title="Růst rychlostí úměrnou velikosti v bezrozměrném čase"
)
plt.legend(title=r"Hodnota $k$");
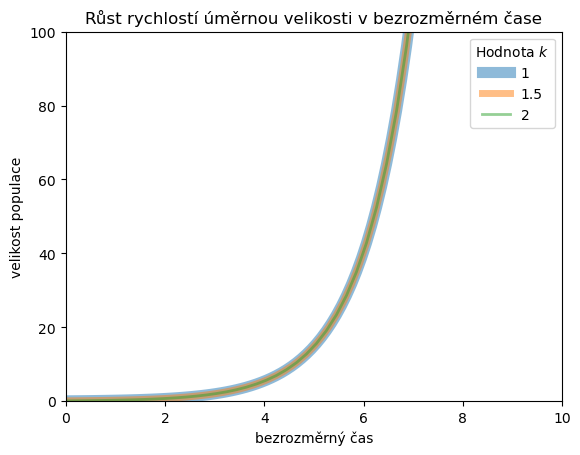
../_images/e5081d3dff41d86c70f59f40d0b86713236bc6864d81a2eacbda07cb0e5f2ece.png

Poznámka: Provnávání grafů je poměrně primitivní metoda. Lepší a jednoznačnější by bylo vypočítat hodnoty v časech, které si odpovídají a poté ukázat, že rozdíl je blízký nule.

5.2. Exponenciální růst k vodorovné asymptotě#

5.2.1. Úkol#

Nakreslete řešení rovnice růstu k vodorovné asymptotě (von Bertalanffyho růst)

\[\frac{\mathrm dx}{\mathrm dt}=k(M-x)\]
pro tři různé hodnoty parametru \(k\). Vytiskněte tabulku s výsledky, vykreslete grafy. Počáteční podmínka bude polovina hodnoty \(M\).

Po splnění modifikujte kód některým z následujících způsobů. Můžete využít umělou inteligenci. Například zápisníky na Anaconda cloud

  • Legendu upravte tak, aby obsahovala Vámi zadaný nadpis a popisky křivek nebyla čísla, ale řetězce „k=x“, kde x je příslušná hodnota parametru.

  • Upravte rozsah tak, aby svislá osa začínala na nule.

  • Upravte graf tak, aby kreslil křivky pro různé hodnoty \(M\).

# Sem vložte řešení.

5.3. Logistický růst - pro případné samostatně pracující studenty#

5.3.1. Úkol#

Vykreslete řešení logistické rovnice

\[\frac{\mathrm dx}{\mathrm dt}=rx\left (1-\frac xK\right)\]
pro cca deset počátečních podmínek rovnoměrně rozmístěných mezi \(0\) a \(K\).

# Sem vložte řešení. Můžete jej rozdělit do více buněk, které si sem vložíte.

5.3.2. Logistická rovnice v bezrozměrném tvaru#

Nyní si ukážeme, že v určitém smyslu stačí bez újmy na obecnosti studovat případ \(K=1\) a \(r=1\). Na rovnici

\[\frac{\mathrm dy}{\mathrm d\tau}=y(1-y)\]
se totiž logistická rovnice transformuje při přechodu od rovnice
\[\frac{\mathrm dx}{\mathrm d t}=rx\left(1-\frac xK\right)\]
s použitím substituce \(y=\frac xK\) a \(\tau = rt\). Najdeme \(y(\tau)\) jako řešení bezrozměrné rovnice s jednotkovými parametry a \(x(t)\) jako řešení rovnice s náhodnými parametry \(r\) a \(K\). Poté ukážeme na několika numerických hodnotách, že platí
\[y(t) = K x(rt).\]

pocatecni_podminka = np.array([0.1])
meze = np.array([0,10])
def rovnice(t, x, r=1, K=1):
    return r*x*(1-x/K)

# r a K budou náhodná čísla z intervalu (0,0.2) a (0,10).
K,r = np.array([10,0.2])*np.random.random(2)
print(f"r={r}, K={K}")
t = np.linspace(*meze,12)

reseni_plne_rovnice = solve_ivp(
                   lambda t,x:rovnice(t,x,r=r,K=K),
                   meze,
                   pocatecni_podminka,
                   t_eval=t
                   )

reseni_bezrozmerne_rovnice = solve_ivp(
                   rovnice,
                   r*meze,  # převod mezí na bezrozměrný čas
                   pocatecni_podminka/K,  # převod na bezrozměrnou velikost populace
                   t_eval=r*t # vyhodnoceni v bezrozmernem case
                   )

df = pd.DataFrame()
df.index = t
df["plnohodnotna"] = reseni_plne_rovnice.y[0]
df["bezrozmerna"] = K*reseni_bezrozmerne_rovnice.y[0] 
df["rozdil"] = np.abs(df["bezrozmerna"]-df["plnohodnotna"])
df["relativni rozdil"] = df["rozdil"]/df["plnohodnotna"]
df

r=0.044855021835722854, K=8.771467972030143
plnohodnotna bezrozmerna rozdil relativni rozdil
0.000000 0.100000 0.100000 0.000000e+00 0.000000e+00
0.909091 0.104113 0.104113 1.539872e-10 1.479045e-09
1.818182 0.108392 0.108392 5.202146e-11 4.799371e-10
2.727273 0.112846 0.112846 7.988885e-09 7.079489e-08
3.636364 0.117479 0.117479 1.276802e-08 1.086832e-07
4.545455 0.122301 0.122301 1.153082e-08 9.428255e-08
5.454545 0.127317 0.127317 7.938103e-09 6.234915e-08
6.363636 0.132536 0.132536 4.559083e-09 3.439889e-08
7.272727 0.137965 0.137965 2.871321e-09 2.081193e-08
8.181818 0.143613 0.143613 3.260737e-09 2.270499e-08
9.090909 0.149489 0.149489 5.021615e-09 3.359196e-08
10.000000 0.155600 0.155600 6.356598e-09 4.085219e-08 
df.rozdil.max()

np.float64(1.2768023693876529e-08)

df["relativni rozdil"].max()

np.float64(1.0868318697605766e-07)

np.isclose(df["bezrozmerna"],df["plnohodnotna"], rtol=0.0001).all()

np.True_
Obsah