8. Autonomní systémy

Co se dozvíte v tomto textu

V této kapitole zkombinujeme aparát lineární algebry a diferenciálních rovnic a budeme se věnovat problematice soustav diferenciálních rovnic. Jedna z aplikací této teorie je modelování interakce dravce a kořisti. Pochopení principů této interakce je zásadní nejenom pro ochranu populace dravce či jeho kořisti, ale také pro zajištění toho, že případné zásahy do této rovnováhy nebudou mít nečekaný efekt. Seznámíme se s takzvaným Volterrovým efektem, kdy se snaha vymýtit nepohodlný živočišný druh může obrátit v populační explozi tohoto druhu.

Foto: Medvěd ulovil kořist. Model dravce a kořisti (nebo analogické modely býložravce a rostliny, případně parazita a hostitele) je jedním ze základních ekologických modelů. Autor Jean Beaufort, https://www.publicdomainpictures.net/.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp
from scipy.signal import find_peaks

Autonomní systémy diferenciálních rovnic jsou soustavy diferenciálních rovnic, kde každá rovnice obsahuje na levé straně derivaci jedné závislé proměnné a na pravé straně funkci všech závislých proměnných. Nezávislou proměnnou je zpravidla čas. To znamená, že pravá strana nezávisí na čase. V případě dvourozměrného autonomního systému se tedy jedná o soustavu diferenciálních rovnic ve tvaru

(8.1)\[\begin{aligned} \frac{\mathrm dx}{\mathrm dt}&= f(x,y), \\ \frac{\mathrm dy}{\mathrm dt}&= g(x,y), \end{aligned} \]

kde \(f\) a \(g\) jsou funkce dvou proměnných. Řešením je dvojice funkcí \(x(t)\) a \(y(t)\), které vyhovují těmto rovnicím. Počáteční podmínku zpravidla formulujeme ve tvaru \(x(0)=x_0\) a \(y(0)=y_0\), kde \(x_0\) a \(y_0\) jsou reálná čísla.

Nejprve se seznámíme s jedním ze základních autonomních systémů používaných v ekologii a poté si zformalizujeme obecný přístup.

8.1. Lotkův–Volterrův model dravce a kořisti

Jednoduchým modelem dravce a kořisti je Lotkův–Volterrův model, který byl sestaven k vysvětlení fenoménu, že při omezení rybolovu během první světové války se v úlovcích zvýšilo procento dravých ryb. Tedy, že omezení rybolovu vedlo k nárůstu populace predátorů. Jinými slovy, lov má pozitivní vliv na populaci kořisti (její relativní velikost vzhledem k populaci dravce), zatímco ukončení lovu má pozitivní vliv na populaci dravce (opět ve smyslu relativní velikosti v porovnání s populací kořisti). Tento efekt se nazývá Volterrův efekt a je jednoduchým důsledkem vzájemné interakce mezi oběma živočišnými druhy.

Model predace

Lotkův–Volterrův model dravce a kořisti byl jedním z prvních úspěšných modelů populační ekologie.

Model vychází z jednoduché myšlenky, že populace kořisti roste rychlostí úměrnou velikosti (neuvažujeme vnitrodruhovou konkurenci, to je realistické například pokud predátor udržuje velikost populace pod nosnou kapacitou prostředí) a kořist je působením predátora odebírána rychlostí úměrnou velikosti populace dravce a populace kořisti (více dravců více omezí růst populace a dravci jsou v lovu úspěšnější, pokud je kořisti více). Populace predátora bez přítomnosti kořisti klesá rychlostí úměrnou velikosti populace predátora a přítomnost kořisti se projeví v růstu populace predátora pozitivním faktorem. Podobně jako u kořisti, předpokládejme, že tento faktor je úměrný velikosti populace kořisti i predátora. Matematicky zapsáno, soužití kořisti a dravce je modelováno soustavou rovnic

\[ \begin{aligned}\frac{\mathrm dx}{\mathrm dt}&=ax-bxy\\\frac{\mathrm dy}{\mathrm dt}&=-cy+dxy\end{aligned} \]

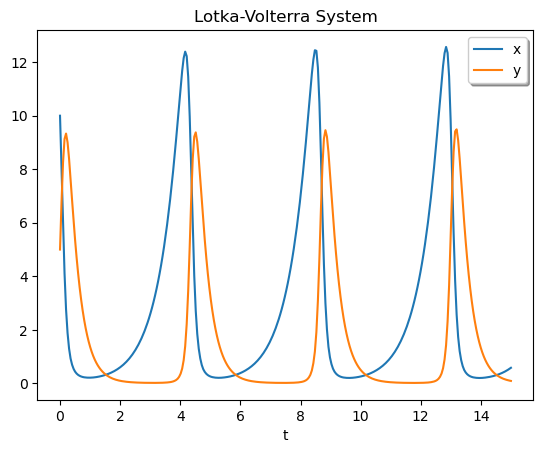
Nápověda příkazu solve_ivp obsahuje řešení Lotkova–Volterrova modelu. Řešení jsou periodické funkce, za maximem kořisti následuje maximum dravce a pokles populace kořisti. Malý stav kořisti způsobí pokles populace dravce, který nemá dost potravy. To uvolní prostor pro růst populace kořisti. Hojnost kořisti ovšem podpoří populaci dravce, která začne se zpožděním růst kopírovat. Mnoho dravců ale hodně uloví a tím se růst populace kořisti zastaví a nastane pokles. Tím se cyklus uzavře.

Show code cell source Hide code cell source

def lotkavolterra(t, z, a, b, c, d):
    x, y = z
    return [a*x - b*x*y, -c*y + d*x*y]

t = np.linspace(0, 15, 300)
sol = solve_ivp(
    lambda t,z:lotkavolterra(t,z, a=1.5, b=1, c=3, d=1), 
    [0, 15], # interval pro reseni
    [10, 5], # pocatecn podminka
    t_eval=t
)

plt.plot(t, sol.y.T)
plt.xlabel('t')
plt.legend(['x', 'y'], shadow=True)
plt.title('Lotka-Volterra System')
plt.show()

Rovnovážný stav systému je řešením soustavy rovnic

\[ \begin{aligned}0&=ax-bxy,\\0&=-cy+dxy.\end{aligned} \]

Za přirozeného předpokladu \(x>0\) a \(y>0\) (obě populace jsou přítomny) je možné tento systém vydělit do tvaru

\[ \begin{aligned}0&=a-by,\\0&=-c+dx,\end{aligned} \]

odkud plyne \(x=\frac cd\) a \(y=\frac ab\). To je zajímavé. Rovnovážný stav kořisti je určen parametry růstu populace dravce a rovnovážný stav dravce je vyjádřen pomocí parametrů růstu populace kořisti.

Pro jiný způsob vizualizace můžeme funkce udávající velikosti populací v čase uvažovat jako parametrické křivky v prostoru dravce a kořisti. Tento prostor se nazývá fázovým prostorem a křivky odpovídající řešení se nazývají trajektorie. Vodorovně budeme vynášet velikost populace kořisti, svisle velikost populace dravce.

Vektor z pravých stran, udávající rychlost růstu populací, je tečným vektorem k trajektoriím. Pokud má tento vektor jednu komponentu nulovou, míří vodorovně nebo svisle a tím stejným směrem míří v daném bodě trajektorie. Vektorové pole definované pravou stranou systému se nazývá směrové pole.

Body, kde je alespoň jedna z pravých stran nulová vytváří v rovině systém křivek, nazývaných nulkliny. Body s nulovou pravou stranou první rovnice odpovídají bodům, ve kterých neroste první populace (kořist) a trajektorie míří svisle. Tyto body vytvoří nulklinu kořisti. Trajektorie protínají nulklinu kořisti svisle. Body s nulovou pravou stranou druhé rovnice tvoří nulklinu dravce a trajektorie ji protínají vodorovně.

V průsečíku nulklin je bod, kdy jsou obě pravé strany nulové a obě populace se nemění (mění se nulovou rychlostí). Tento bod se nazývá stacionární bod a odpovídá konstantnímu řešení. Ostatní nekonstantní řešení okolo stacionárního bodu obíhají v cyklech.

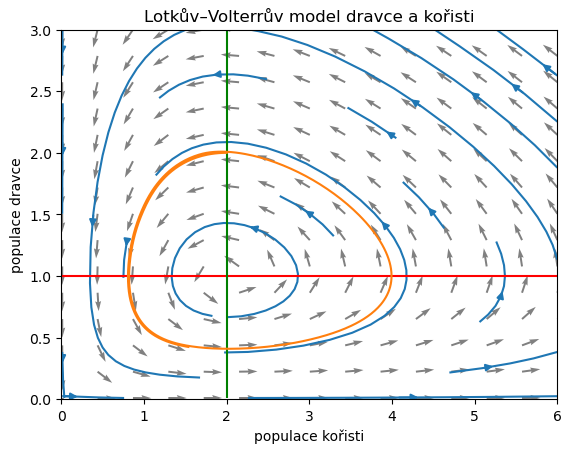
Pro více informací zakreslíme do fázového prostoru nejenom řešení, ale i nulkliny a směrové pole. Nulklinou kořisti (křivka kdy je růst kořisti nulový) je přímka \(y=a/b\), tj. vodorovná přímka procházející stacionárním bodem. Každá trajektorie tuto přímku protíná svisle. Nulklinou dravce (křivka kdy je růst dravce nulový) je přímka \(x=c/d\), tj. svislá přímka procházející stacionárním bodem. Každá trajektorie tuto přímku protíná vodorovně. Všechny trajektorie jsou uzavřené cykly. Na obrázku je několik částí těchto trajektorií vykreslených příkazem streamplot a jedna celá trajektorie ve tvaru cyklu.

Show code cell source Hide code cell source

def korist(x,y,a=1,b=1):
    return a*x - b*x*y

def dravec(x,y,c=1,d=0.5):
    return -c*y+d*x*y

def model(t,X,a=1,b=1,c=1,d=0.5):
    x,y = X
    return [korist(x,y,a,b),dravec(x,y,c,d)]
meze = [0,10]
pocatecni_podminka = [2,2]

xmax = 6
ymax = 3
x, y = np.meshgrid(np.linspace(0.01, xmax, 15), 
                   np.linspace(0.01, ymax, 15))

# Komponenty vektoroveho pole
u,v = model(0,[x,y])
M = np.sqrt(u**2+v**2) # velikost vektoru

fig,ax = plt.subplots()
ax.quiver(x,y,u/M,v/M,color='gray',units='xy', angles='xy') # vykresleni s jednotkovou delkou
integralni_krivky = ax.streamplot(x, y, u, v, density=0.3)

t = np.linspace(*meze,800)
reseni = solve_ivp(model,
                   meze,
                   pocatecni_podminka,
                   t_eval = t
                  )

x, y = np.meshgrid(np.linspace(0.01, xmax, 40), 
                   np.linspace(0.01, ymax, 40))

x_nulcline = plt.contour(x, y, korist(x,y), [0], colors='red')
y_nulcline = plt.contour(x, y, dravec(x,y), [0], colors='green')

ax.plot(*reseni.y)
ax.set(
    ylim=(0,None), 
    xlim=(0,None),
xlabel="populace kořisti",
ylabel="populace dravce",
title="Lotkův–Volterrův model dravce a kořisti");

8.2. Volterrův efekt

Na uvedeném modelu si můžeme demonstrovat Volterrův efekt. Toto je situace, kdy zásah proti škůdcům s cílem redukovat jejich populaci může v dlouhodobém měřítku paradoxně vyvolat přemnožení těchto škůdců. Například použití insekticidu nebo pesticidu může krátkodobé snížit populaci, kterou se snažíme redukovat, ale pokud jsou na použitou látku citliví i predátoři, živící se tímto škůdcem, dojde k výrazné redukci i u populace predátorů. To znamená, že škůdce ztratí svého přirozeného nepřítele a tím je mu umožněn nejen nárůst na původní hodnoty, ale i přemnožení. V konečném důsledku dojde k přemnožení populace škůdce, jehož počty jsme postřikem chtěli redukovat

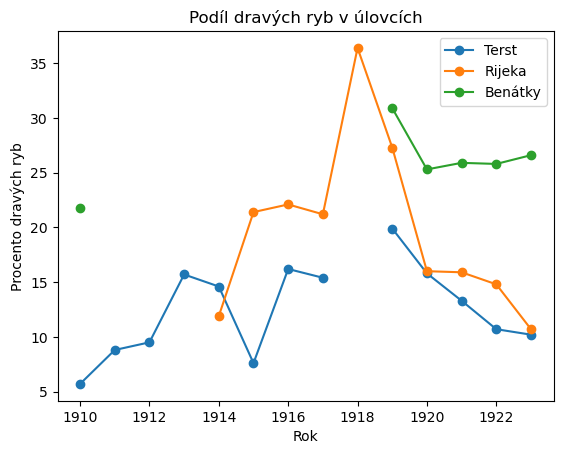
Volterrův efekt byl vlastně i motivací pro sestavení modelu. Na tento efekt a zajímavé zvýšení procenta dravých ryb v sítích po omezení rybolovu během první světové války Volterru upozornil jeho zeť, biolog Umberto d’Ancona.

Show code cell source Hide code cell source

data = {
    'Rok':np.arange(1910,1924),
    'Terst':[5.7, 8.8, 9.5, 15.7, 14.6, 7.6, 16.2, 15.4, None, 19.9, 15.8, 13.3, 10.7, 10.2],
    'Rijeka':[None, None, None, None, 11.9, 21.4, 22.1, 21.2, 36.4, 27.3, 16.0, 15.9, 14.8, 10.7],
    'Benátky':[21.8, None, None, None, None, None, None, None, None, 30.9, 25.3, 25.9, 25.8, 26.6]
}
df = pd.DataFrame(data)
ax = df.plot(x="Rok",style="o-")
ax.set(title="Podíl dravých ryb v úlovcích", ylabel="Procento dravých ryb");
# Podle Nicolas Bacaër, A Short History of Mathematical Population Dynamics

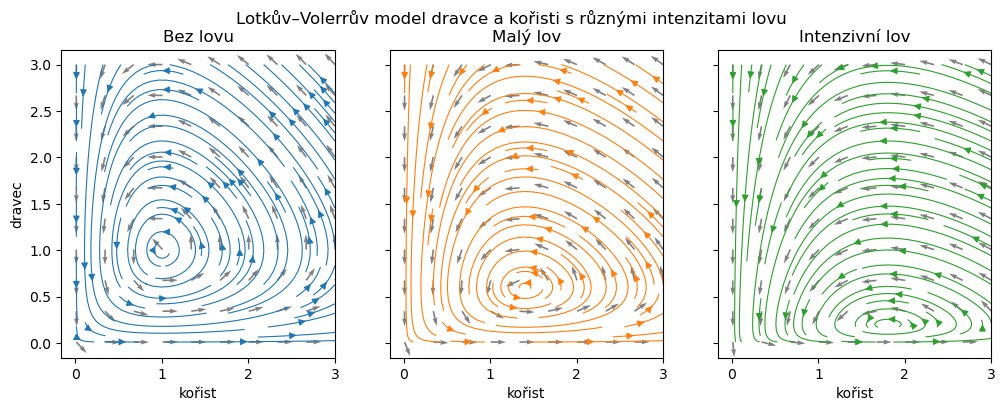
Budeme základní model modifikovat tak, že do populace kořisti i dravce přidáme lov s konstantním úsilím, tj. úměrný lovené populaci. Například pro lov ryb to věrně modeluje situaci, že procento dravých ryb uvízlých v rybářských sítích roste s tím, jak roste procento dravých ryb v mořích celkově.

Nepovedený boj se škůdci

Jako lov můžeme interpretovat i jiné odstraňování části populace. Je-li hmyzí škůdce kořistí pro predátora, můžeme i likvidaci tohoto škůdce použitím insekticidů interpretovat jako lov. Pokud insekticid působí i na predátora, je situace stejná jako u Lotkova–Volterrova modelu s lovem obou populací. Lov paradoxně zvýší populaci kořisti, tedy škůdce. Ochrana před škůdcem pomocí insekticidu má tedy přesně opačný účinek.

Například první komerční postřik para-oxonem nesmírně účinně hubil v Anglii populace mšice zelné, Brevicoryne brassicae. Že však současně byli ničeni i přirození nepřátelé, vedlo do dvou týdnů k největší populační explozi tohoto druhu mšice v celé anglické historii ([3] str. 564).

Fázový portrét ukazuje, že s vyšší intenzitou lovu se stacionární bod, okolo kterého trajektorie obíhají, posunuje doprava dolů. Tedy do míst s vyšší populací kořisti a menší populací dravce.

Show code cell source Hide code cell source

def predator(x,y,c=1,d=1,h=0):
    return -c*y + d*x*y - h*y

def prey(x,y,a=1,b=1,h=0):
    return a*x - b*x*y - h*x

def model(t,X,h=0,a=1,b=1,c=1,d=1):
    x,y = X
    return [prey(x,y,a,b,h),predator(x,y,c,d,h)]

xmax = 3
ymax = 3
x, y = np.meshgrid(np.linspace(0.01, xmax, 10), 
                   np.linspace(0.01, ymax, 10))

fig,axs = plt.subplots(1,3,sharex=True, sharey=True, figsize=(12,4))

for i,h in enumerate([0,0.4,0.8]):
    u,v = model(0,[x,y],h)
    M = np.sqrt(u**2+v**2) # velikost vektoru
    ax = axs[i]
    ax.quiver(x,y,u/M,v/M,color='gray',units='xy', angles='xy') # vykresleni s jednotkovou delkou
    ax.streamplot(x, y, u, v, density=1, color=f"C{i}", linewidth=0.8)

axs[0].set(
    xlabel="kořist",
    ylabel="dravec",
    title="Bez lovu"
);
axs[1].set(
    xlabel="kořist",
    title="Malý lov"
)
axs[2].set(
    xlabel="kořist",
    title="Intenzivní lov"
)
plt.suptitle("Lotkův–Volerrův model dravce a kořisti s různými intenzitami lovu");

Pro kontrolu ještě prozkoumáme časový vývoj populací pro různé intenzity lovu. Výpočty uložíme do tabulky s hierarchickým indexováním sloupců a poté vykreslíme a použijeme k výpočtu střední hodnoty.

Show code cell source Hide code cell source

def predator(x,y,c=1,d=1,h=0):
    return -c*y + d*x*y - h*y

def prey(x,y,a=1,b=1,h=0):
    return a*x - b*x*y - h*x

def model(t,X,h=0,a=1,b=2,c=1,d=1):
    x,y = X
    return [prey(x,y,a,b,h),predator(x,y,c,d,h)]

pocatecni_podminka = [0.5,0.4]
meze = [0,30]
t=np.linspace(*meze, 500)  
lovy = [0,0.25,0.5]
druhy_populaci = ["kořist","dravec"]

idx = pd.MultiIndex.from_tuples([],names = ['intenzita lovu','nazev populace'])
df = pd.DataFrame(columns=idx, index=t)

for h in lovy:
     df[[(h,kdo) for kdo in druhy_populaci]] = solve_ivp(
                   lambda t,x:model(t,x,h=h),
                   meze,
                   pocatecni_podminka,
                   t_eval=t,
                   ).y.T
df.head()        

intenzita lovu	0.00		0.25		0.50
nazev populace	kořist	dravec	kořist	dravec	kořist	dravec
0.000000	0.500000	0.400000	0.500000	0.400000	0.500000	0.400000
0.060120	0.506409	0.388228	0.499032	0.382351	0.491761	0.376564
0.120240	0.513611	0.376957	0.499101	0.365472	0.484981	0.354344
0.180361	0.521600	0.366181	0.500137	0.349361	0.479437	0.333339
0.240481	0.530374	0.355895	0.502101	0.334001	0.475045	0.313506

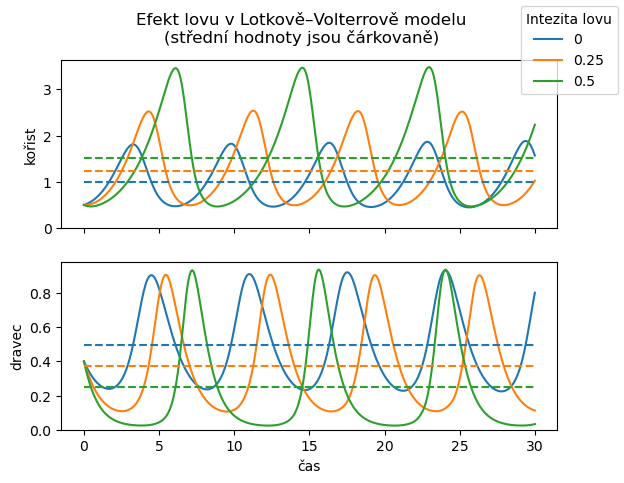
Data vykreslíme, najdeme střední hodnotu a tuto střední hodnotu přidáme do obrázku. Můžeme sledovat, jaký má lov vliv na oscilace (jejich amplitudu a frekvenci) a zejména na střední hodnotu, okolo které řešení oscilují. Matematickým rozborem je možné ukázat, že střední hodnota je vlastností daného autonomního systému a je pro všechna řešení stejná a shoduje se se stacionárním bodem. Naproti tomu amplituda a frekvence se u různých řešení téhož autonomního systému může lišit.

Show code cell source Hide code cell source

# Dva obrázky nad sebou se sdílenou vodorovnou osou
fig,ax = plt.subplots(2,1,sharex=True)

# Grafy do dvou obrázků podle druhu populace
for a,kdo in zip(ax,druhy_populaci):
    data = df.xs(level=1,key=kdo, axis=1)
    a.plot(t,data)
    a.set(ylabel=kdo, ylim=(0,None))   

# Výpočet středních hodnot a vykreslení do grafu
for a,kdo in zip(ax,druhy_populaci):    # Cyklus přes populace
    for j,h in enumerate(lovy):            # Cyklus přes intenzity lovu
        data = df[h,kdo]          # Data pro danou populaci a intenzitu lovu
        meze = find_peaks(data)[0][0:2]  # Nalezení prvních dvou maxim
        prumer = np.mean(data.iloc[meze[0]:meze[1]]) # Průměrná hodnota
        a.plot([t[0],t[-1]],[prumer,prumer],"--", color=f"C{j}")
        
fig.legend(lovy,title="Intezita lovu")    
ax[1].set(xlabel="čas")
plt.suptitle("Efekt lovu v Lotkově–Volterrově modelu\n(střední hodnoty jsou čárkovaně)");

8.3. Střípky z obecné teorie autonomních systémů

8.3.1. Lineární autonomní systémy

Soustava \(n\) diferenciálních rovnic tvaru

\[\frac{\mathrm dX}{\mathrm dt}=AX + B,\]

kde \(X\) a \(B\) jsou \(n\)-rozměrné sloupcové vektory a \(A\) je \(n\)-rozměrná čtvercová matice je lineární autonomní systém.

Je-li \(X_0\) řešením rovnice

\[AX+B=0,\]

je konstantní funkce \(X(t)=X_0\) řešením této rovnice. Toto řešení se nazývá stacionární bod.

Protože po substituci \(Y=X-X_0\) se rovnice transformuje na rovnici

\[\frac{\mathrm dY}{\mathrm dt}=AY,\]

můžeme bez újmy na obecnosti předpokládat, že \(B\) je nulový vektor a studovat rovnici ve tvaru

(8.2)\[ \frac{\mathrm dX}{\mathrm dt}=AX \]

se stacionárním bodem v počátku. Rovnice má následující vlastnosti.

• Lineární kombinace libovolného počtu řešení rovnice (8.2) je také řešením této rovnice.

• Je-li \(\lambda\) vlastním číslem matice \(A\) a \(U\) je příslušný vlastní vektor, je funkce \(X(t)=e^{\lambda t}U\) řešením rovnice (8.2). Jsou-li \(\lambda\) a \(U\) komplexní, je řešením rovnice samostatně reálná i imaginární část.

Chování řešení pro případ záporného vlastního čísla nebo čísla se zápornou reálnou částí charakterizuje následující graf. Zjednodušeně řečeno, řešení konverguje k nule buď monotonně (reálná vlastní hodnota) nebo v oscilacích (komplexní vlastní hodnota).

Show code cell source Hide code cell source

l = -.5+4j
t = np.linspace(0,10,500)
plt.plot(t,np.exp(l*t).real,label="reálná část komplexní exponenciely")
plt.plot(t,np.exp(l*t).imag,label="imaginární část komplexní exponenciely")
plt.plot(t,np.exp(l.real*t),label="reálná exponenciela")
plt.legend()
plt.title("Exponenciální funkce s exponentem se zápornou reálnou částí");

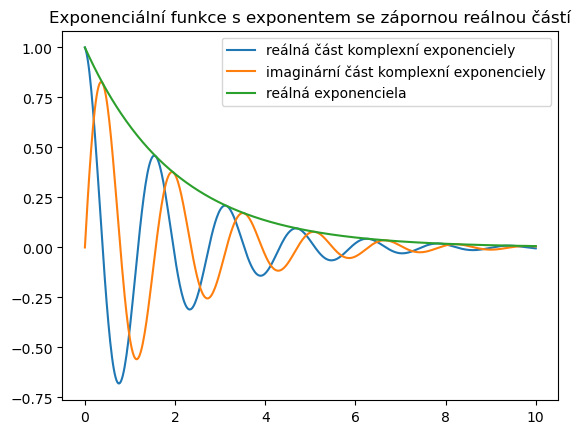
Experimentem s uvedeným kódem je možné ověřit, že vetší imaginární část se projeví zrychlením oscilací a více záporná reálná část se projeví zrychlením poklesu. Podobné grafy je možno nakreslit i pro kladnou vlastní hodnotu nebo pro vlastní hodnotu s kladnou reálnou částí. Rozdíl je v tom, že v takovém případě řešení buď roste do nekonečna, nebo osciluje se stále větší amplitudou.

8.3.2. Nelineární autonomní systémy

Soustava

\[X'=F(X)\]

diferenciálních rovnic, kde pravé strany nezávisí na čase, se nazývá autonomní systém.

Je-li \(F(X_0)=0\), je možno systém v okolí bodu \(X_0\) aproximovat lineárním systémem

\[X'=J(X_0)(X-X_0),\]

kde \(J(X_0)\) je Jacobiho matice funkce \(F(X)\) v bodě \(X_0\), tj. pro \(F(X)=(F_1(X),\dots,F_n(X))^T\) je

\[J(X_0)=\left(\frac{\partial F_i(X_0)}{\partial x_j}\right).\]

O chování trajektorií v okolí stacionárního bodu tedy rozhodnou vlastní čísla Jacobiho matice. Za předpokladu, že jsme relativně daleko od případů, kdy se mění typ stacionárního bodu, tj. vlastní čísla jsou navzájem různá, jsou nenulová a v případě komplexních vlastních čísel mají nenulové reálné části, má původní nelineární systém stejný typ stacionárního bodu jako lineární systém s Jacobiho maticí. Nelineární systém tedy v jistém smyslu „zdědí“ chování řešení od své lineární aproximace pomocí Jacobiho matice. Je však nutno připomenout, že aproximace pomocí Jacobiho matice je jenom lokální a můžeme takto posoudit jenom řešení z nějakého okolí stacionárního bodu.

Zejména tedy, pokud má Jacobiho matice všechny vlastní hodnoty záporné, tak všechna řešení z nějakého okolí stacionárního bodu konvergují do tohoto bodu. Pokud má všechny vlastní hodnoty kladné, všechna řešení z nějakého okolí se naopak od stacionárního bodu vzdalují. To platí i pro vlastní komplexní vlastní hodnoty, pouze se mezi konvergencí a vzdalování přepíná podle znaménka reálné části vlastních hodnot a řešení oscilují směrem ke stacionárnímu bodu nebo od něj.

8.3.3. Autonomní systémy v rovině

Pro autonomní systém v rovině (8.1) je možné chápat řešení jako parametricky zadané rovinné křivky. Tyto křivky se nazývají trajektorie. Trajektorie buď konvergují do nějakého stacionárního bodu, nebo mají alespoň jednu ze složek neohraničenou, nebo konvergují k nějakému cyklu. Vektorové pole definované vektorovou funkcí na pravé straně autonomního systému je tvořeno šipkami, které míří stejným směrem jako trajektorie. Toto pole se nazývá směrové pole autonomního systému a umožňuje odhadnout chování trajektorií a tím i chování řešení. Na rozdíl od směrového pole diferenciální rovnice, směrové pole autonomního systému může obsahovat i šipky mířící doleva.

Vizualizaci řešení autonomního systému tedy můžeme provést dvěma způsoby.

• Vykreslit obě komponenty řešení jako funkce nezávislé proměnné. Výsledkem jsou tedy dvě křivky udávající časový průběh každé z komponent řešení.

• Vykreslit řešení jako parametrickou křivku. Výsledkem je tedy jedna křivka, ze které jsou patrné stavy, kterými systém postupně prochází, ale nemáme informaci o čase. Tato varianta je běžně používána a proto ji rozebereme níže.

Obecný tvar autonomního systému v rovině je

\[\begin{aligned}\frac{\mathrm dx}{\mathrm dt}&=f(x,y)\\\frac{\mathrm dy}{\mathrm dt}&=g(x,y)\\\end{aligned}.\]

Křivka nebo křivky vyhovující rovnici

\[f(x,y)=0\]

se nazývají \(x\)-nulkliny a v průsečíku trajektorie a \(x\)-nulkliny míří trajektorie svisle (hodnota \(x\) se mění nulovou rychlostí).

Křivka nebo křivky vyhovující rovnici

\[g(x,y)=0\]

se nazývají \(y\)-nulkliny a v průsečíku trajektorie a \(y\)-nulkliny míří trajektorie vodorovně (hodnota \(y\) se mění nulovou rychlostí).

V průsečíku nulklin je stacionární bod.

Jacobiho matice

\[J(x,y)=\begin{pmatrix} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} \\ \frac{\partial g}{\partial x} & \frac{\partial g}{\partial y} \end{pmatrix}\]

definuje lineární systém, který má v okolí každého bodu stejné chování trajektorií jako systém nelineární. Toto má smysl dělat ve stacionárních bodech a podle vlastních čísel Jacobiho matice v těchto stacionárních bodech rozhodneme o chování trajektorií. (Mimo stacionární body je situace triviální, trajektorie míří směrem definovaným pravou stranou systému a proto linearizaci nepotřebujeme.)

Vlastní čísla Jacobiho matice ve stacionárním bodě jsou dvě a pokud jsou komplexními čísly, potom mají stejnou reálnou část a imaginární část se liší znaménkem. To znamená, že je jenom několik málo druhů možného chování trajektorií v okolí stacionárních bodů. To dovoluje stacionární body klasifikovat podle toho, zda přitahují či odpuzují trajektorie ze svého okolí a zda toto přitahování či odpuzování souvisí s přikloněním se k nějakému pevnému směru, nebo zda je realizováno oscilacemi s měnící se amplitudou.

Autonomní systém v rovině

Dvourozměrné autonomní systémy můžeme analyzovat metodami založenými na klasifikaci stacionárních bodů. Typ stacionárního bodu (uzel, ohnisko, …) a jeho stabilitu poznáme u lineárního systému z vlastních čísel matice, u nelineárního z vlastních čísel Jacobiho matice.

• Stabilní uzel je stacionární bod takový, že pro \(t\to\infty\) všechny trajektorie z nějakého okolí konvergují do tohoto bodu bez oscilací. Nestabilní uzel má stejnou vlastnost, ale pro \(t\to-\infty\), tedy trajektorie z tohoto bodu vycházejí. Stabilní uzel poznáme podle dvou záporných a nestabilní uzel podle dvou kladných reálných vlastních hodnot.

• Stabilní a nestabilní ohnisko je stacionární bod se stejnou vlastností jako uzel, ale konvergence je spojena s oscilacemi okolo stacionárního bodu. Stabilní ohnisko poznáme podle dvou komplexně sdružených vlastních hodnot se zápornou reálnou částí, nestabilní ohnisko s kladnou reálnou částí.

• Sedlo je stacionární bod, který má v každém okolí pouze konečný počet trajektorií, které pro \(t\to\pm\infty\) konvergují k tomuto bodu. Poznáme jej podle jedné kladné a jedné záporné vlastní hodnoty.

• Bod rotace je takový bod, v jehož každém okolí jsou cykly. Pokud navíc v nějakém okolí existují pouze cykly, nazývá se tento bod navíc střed. Bod rotace souvisí s komplexně sdruženými vlastními čísly s nulovou reálnou částí, ale v těchto případech může stacionární bod být i ohniskem.