Ctrl+K

Diferenciální rovnice 3

6. Diferenciální rovnice 3#

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.integrate import solve_ivp

6.1. Lov v logistické rovnici#

6.1.1. Konstantní užitek#

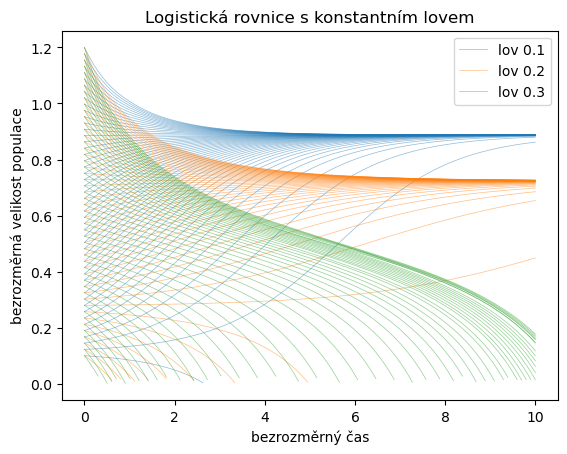
V logistické rovnici nakreslíme pro tři různé intenzity lovu průběh řešení. Prorovnejte následující kód s kódem pro kreslení řešení jedné sady pro jednu intenzitu lovu.

Zpravidla netriviální kód nenapíšeme napoprvé, ale musíme příkazy ladit. V následujícím jsou rozděleny fáze řešení rovnice a vykreslení řešení. Pro potřeby spouštění je po odladění vhodné buňky sloučit.

  • Zkuste si v následující buňce rozdělit kód do dvou různých buněk. Tedy přepnete se do editace, najdete vhodný řádek a v menu vyberete „Edit“ a „Split Cell“.

  • Poté zkuste buňky co se mají spouštět společně spojit. V příkazovém modu buňky označte (například shift + šipka nahoru nebo dolů) a stisknout velké M, tj. Shift + M. Pozor, pokud byste stiskli malé „m“, buňka by se změnila na Markdown buňku s textem. Zpět na buňku s kódem je klávesa „y“.

pocatecni_podminka = np.linspace(0.1,1.2,50)
meze = [0,10]
t = np.linspace(*meze,100)

def destrukce_populace(t,x):  # Pokud x klesne na nulu, zastavíme výpočet
    return x
destrukce_populace.terminal = True

def rovnice(t, x, r=1, K=1, h=0.15):
    return r*x*(1-x/K)-h

lovy = [0.1,0.2,0.3]
# Pro různé počáteční podmínky se bude lišit interval, 
# na kterém algoritmus najde řešení. Proto nemůžeme data
# shrnout do jedné tabulky. Alternativou je tabulka s 
# nedefinovanými hodnotami, viz
# https://robert-marik.github.io/dmp/snippety/tabulky_none.html
# a https://robert-marik.github.io/dmp/snippety/multiindex.html
reseni = [
        [ solve_ivp(
                   lambda t,x:rovnice(t,x,h=h),
                   meze,
                   [pp],
                   t_eval=t,
                   events=destrukce_populace,  # zastavení výpočtu při poklesu populace na nulu
                   )
          for pp in pocatecni_podminka]
        for h in lovy]

# GRAFICKA PREZENTACE VYSLEDKU
fig,ax = plt.subplots()
for i,r in enumerate(reseni):
    for res in r:
        ax.plot(res.t,res.y[0], color=f"C{i}", alpha=0.5, label=f"lov {lovy[i]}", lw=0.5)
ax.set(
  title="Logistická rovnice s konstantním lovem",
  xlabel="bezrozměrný čas",
  ylabel="bezrozměrná velikost populace"
  );

# Návod jak seskupit položky legendy je na https://stackoverflow.com/questions/26337493/pyplot-combine-multiple-line-labels-in-legend
handles, labels = ax.get_legend_handles_labels()
labels, ids = np.unique(labels, return_index=True)
handles = [handles[i] for i in ids]
plt.legend(handles, labels);
../_images/94a43d98e82d838c5f1d605323fb8653da17b95d6cd7bdcae3518ab127825d5f.png 
fig,ax = plt.subplots()
x = np.linspace(0,1)
plt.plot(x,rovnice(0, x,h=0),label="růst bez lovu",color='r')
for h in lovy: 
    plt.plot(x,h+0*x,label=f"lov {h}")
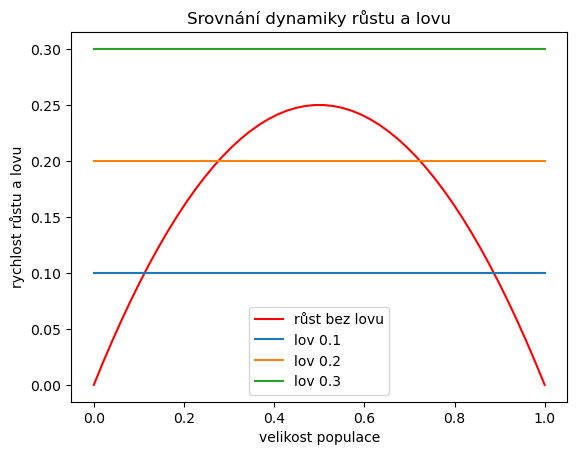
ax.set(
    xlabel="velikost populace",
    ylabel="rychlost růstu a lovu",
    title="Srovnání dynamiky růstu a lovu"
)    
plt.legend()    

<matplotlib.legend.Legend at 0x7f30dd93a8d0>
../_images/837ea6c02646f161ba6fba6dde11a6dd47fd8f0f2a0af837bf0c59c854aa2e51.png

6.1.2. Konstantní úsilí#

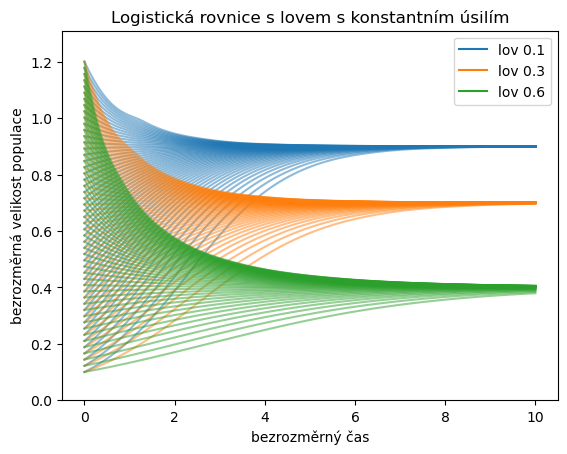
Modifikujte předchozí kód s vykreslením časového vývoje populace vystavené lovu. Lov konstantní intenzitou nahraďte lovem s konstantním úsilím. Zkuste nejprve minimální úprava kódu. Bez ohledu na efektivitu, vyjděte z předchozího a snažte se co nejméně modifikovat výchozí kód. Poté si prostudujte elegantnější přístup využívající toho, že žádné řešení neskončí v konečném čase.

# sem napiste reseni

U konstantního úsilí není problém s tím, že by některá řešení končila dříve. Proto může být programový kód kratší a čistý. Například nemusíme pracovat s vnořenými cykly a můžeme příkazu solve_ivp poslat současně všechny počáteční podmínky. Pokusme se o to.

pocatecni_podminka = np.linspace(0.1,1.2,51).round(3)
meze = [0,10]
t = np.linspace(*meze,100)

def rovnice(t, x, r=1, K=1, h=0.15):
    return r*x*(1-x/K)-h*x

lovy = [0.1,0.3,0.6]

### Definice tabulky s víceúrovňovými nadpisy sloupců, MultiIndex
### https://pandas.pydata.org/docs/user_guide/advanced.html
iterables = [lovy,pocatecni_podminka]
my_index = pd.MultiIndex.from_product(iterables, names=['lov', 'poč.podm.'])
df = pd.DataFrame(columns=my_index)
df["čas"] = t
for h in lovy:
    r = solve_ivp(
              lambda t,x:rovnice(t,x,h=h),
              meze,
              pocatecni_podminka,
              t_eval=t,
              ).y.T
    df[[(h,i) for i in pocatecni_podminka]]=pd.DataFrame(r)

df.set_index("čas", inplace=True)
df.T
čas 0.000000 0.101010 0.202020 0.303030 0.404040 0.505051 0.606061 0.707071 0.808081 0.909091 ... 9.090909 9.191919 9.292929 9.393939 9.494949 9.595960 9.696970 9.797980 9.898990 10.000000
lov poč.podm.
0.1 0.1 0.100 0.108371 0.117336 0.126920 0.137151 0.148054 0.159650 0.171950 0.184964 0.198694 ... 0.898016 0.898182 0.898329 0.898459 0.898573 0.898675 0.898768 0.898856 0.898940 0.899027
0.122 0.122 0.131909 0.142472 0.153707 0.165637 0.178276 0.191634 0.205712 0.220505 0.236000 ... 0.898404 0.898538 0.898656 0.898760 0.898852 0.898934 0.899008 0.899078 0.899147 0.899216
0.144 0.144 0.155339 0.167371 0.180106 0.193555 0.207723 0.222605 0.238190 0.254458 0.271383 ... 0.898676 0.898787 0.898885 0.898971 0.899047 0.899115 0.899177 0.899235 0.899291 0.899349
0.166 0.166 0.178662 0.192036 0.206123 0.220922 0.236423 0.252609 0.269455 0.286929 0.304989 ... 0.898878 0.898972 0.899055 0.899128 0.899192 0.899250 0.899302 0.899351 0.899399 0.899448
0.188 0.188 0.201879 0.216470 0.231766 0.247752 0.264403 0.281690 0.299574 0.318011 0.336948 ... 0.899034 0.899115 0.899186 0.899249 0.899304 0.899354 0.899399 0.899441 0.899482 0.899524
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
0.6 1.112 1.112 1.038781 0.976482 0.922880 0.877138 0.838270 0.805131 0.776418 0.750671 0.726294 ... 0.407163 0.406875 0.406598 0.406333 0.406079 0.405835 0.405601 0.405376 0.405161 0.404954
1.134 1.134 1.057181 0.991996 0.936033 0.888480 0.848319 0.814316 0.785022 0.758774 0.733722 ... 0.407263 0.406970 0.406690 0.406421 0.406163 0.405915 0.405678 0.405450 0.405232 0.405022
1.156 1.156 1.075507 1.007379 0.949009 0.899631 0.858199 0.823389 0.793589 0.766905 0.741191 ... 0.407361 0.407065 0.406780 0.406508 0.406246 0.405995 0.405755 0.405524 0.405303 0.405090
1.178 1.178 1.093759 1.022631 0.961806 0.910585 0.867910 0.832358 0.802137 0.775090 0.748730 ... 0.407459 0.407159 0.406871 0.406594 0.406329 0.406075 0.405831 0.405597 0.405373 0.405157
1.2 1.200 1.111938 1.037750 0.974419 0.921339 0.877452 0.841232 0.810687 0.783359 0.756369 ... 0.407558 0.407253 0.406961 0.406681 0.406412 0.406155 0.405908 0.405671 0.405443 0.405225

153 rows × 100 columns

fig,ax = plt.subplots()
for i in range(len(lovy)): # tři čáry mimo obrázek kvůli legendě
    ax.plot([0,1],[-1,-1],label=f"none")
for i,h in enumerate(lovy):
    ax.plot(df.index,df[h], color=f"C{i}", alpha=0.5)
ax.set(
  title="Logistická rovnice s lovem s konstantním úsilím",
  xlabel="bezrozměrný čas",
  ylabel="bezrozměrná velikost populace",
  ylim=[0,None]
  )

plt.legend([f"lov {lov}" for lov in lovy]);
../_images/ded9d62567018c6de0785915d6cb3e5417281722dfd701df45564d71dc67c5ae.png 
fig,ax = plt.subplots()
x = np.linspace(0,1)
plt.plot(x,rovnice(0, x,h=0),label="růst bez lovu")
for a in lovy: 
    plt.plot(x,a*x,label=f"lov {a}")
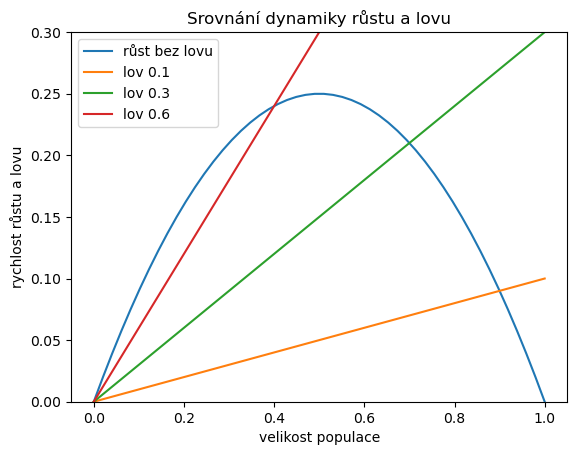
ax.set(
    xlabel="velikost populace",
    ylabel="rychlost růstu a lovu",
    title="Srovnání dynamiky růstu a lovu",
    ylim=(0,0.3)
)    
plt.legend() 

<matplotlib.legend.Legend at 0x7f30d440c440>
../_images/642162c6f925949560a6a6f4c3edf344772af3573a3d6adeab8c0da6b3eb66b9.png

6.2. Alleeho efekt#

Nakreslete model řešení rovnice modelující lov konstantním úsilím v populaci s Alleeho efektem. Můžete uvažovat slabý Aleeho efekt (pro malé velikosti populace se dynamika růstu výrazně zpomalí) nebo silný Alleeho efekt (pro malé velikosti populace vymírá). Můžete použít například rovnici

\[\frac{\mathrm dx}{\mathrm dt} = rx ^k\left(1-\frac xK\right) -ax, \quad k>1\]
pro slabý nebo
\[\frac{\mathrm dx}{\mathrm dt} = rx \left(1-\frac xK\right)\left(\frac xA-1\right) -ax, \quad 0<A<K\]
pro silný Alleeho efekt. Nejprve si nakreslete křivky růstu a lovu, pro vytipování vhodných numerických hodnot pro parametry a poté nakreslete řešení diferenciální rovnice pro různé intenzity lovu a různé počáteční podmínky.

# sem napiste kod pro vykreslení krivek rustu a lovu

# sem napiste kod pro vykreslení reseni diferenciální rovnice

6.3. Populace pod predačním tlakem#

Vykreslete model pro populaci pro predačním tlakem https://robert-marik.github.io/dmp/prednaska/05.html#populace-pod-predacnim-tlakem. Použijte bezrozměnrou formulaci, tj. rovnici

\[\frac{ \mathrm dx}{ \mathrm d\tau}=\alpha\left(1-\frac {x}{\beta}\right)x-\frac {x^2}{x^2+1}.\]
Tři dvojice hodnot pro \(\alpha\) a \(\beta\) můžete použít z https://robert-marik.github.io/dmp/prednaska/05.html#rustove-krivky.

# sem napiste reseni
Obsah