1. Data a grafy#
1.1. První kroky#
Komentáře budou jenom stručné, pokud chcete podrobné vysvětlení jednotlivých příkazů, můžete je vykopírovat do nějakého nástroje umělé inteligence, například ChatGPT nebo ZZZ Code AI. Oba nástroje umí komunikovat i v češtině.
Co googlit
Klíčová slova, která se hodí pro dotazy pro vyhledávací službu. Pro potřeby nalezení návodů, tutoriálů, tipů, uživatelského manuálu apod.
Slovo, fráze |
Použití |
|---|---|
Python |
Programovací jazyk, který budeme používat |
Jupyter, JupterLab |
Prostředí, ve kterém budeme Python používat nejčastěji. Prostředí pro práci je mnoho, volíme takové, které nevyžaduje instalaci na lokální PC. |
NumPy |
Knihovna numerické výpočty. |
SciPy |
Knihovna pro řešení diferenciálních rovnic a pro mnoho dalšího. |
|
Příkaz z knihovny SciPy pro řešení diferenciálních rovnic. |
Matplotlib |
Knihovna pro kreslení obrázků, grafů. Nejčastěji použijeme pro vizualizaci výstupu přkazu |
Pandas |
Knihovna pro práci s tabulkami. |
dataframe |
Název pro tabulky používaný při práci s knihovnou Pandas. |
difefrenciální rovnice, počáteční úloha, ODE, ordinary differential equation, IVP, initial value problem |
Název matematických nástrojů používaný při modelování |
Markdown |
Jeden z nejjednodušších značkovacích jazyků, používá se pro doprovodné texty v Jupyter zápisnících |
LaTeX, \(\LaTeX\), latex |
Nejrychlejší a nejspolehlivější metoda psaní matematických výrazů do textu, kompatibilní s Markdown a s relativně nedávnou verzí MS Word. Také samostatný typografický systém, ale my budeme využívat jenom pro psaní matematických výrazů, kde je LaTeX nenahraditelný. |
# načtení knihoven
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
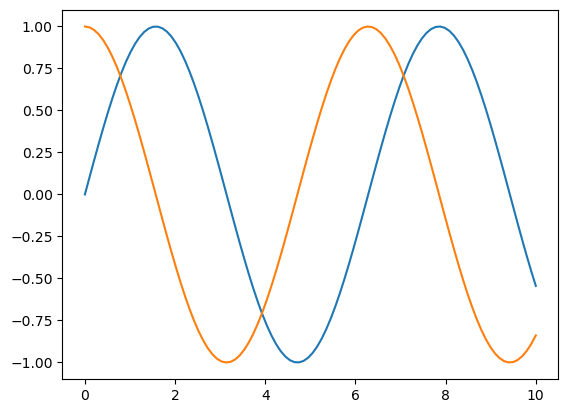
# vytvoření pole pro definiční obor a vykreslení dvou goniometrickcýh funkcí
x = np.linspace(0,10,100)
plt.plot(x,np.sin(x))
plt.plot(x,np.cos(x))
[<matplotlib.lines.Line2D at 0x7fa3360f4b90>]
# vytvoření pole pro definiční obor a vykreslení dvou goniometrickcýh funkcí
pocet_bodu = 100
a,b = 0, 10
x = np.linspace(a,b,pocet_bodu)
plt.plot(x,np.sin(x))
plt.plot(x,np.cos(x))
[<matplotlib.lines.Line2D at 0x7fa335fce350>]

Při skutečné práci chceme zpravidla oddělit načtení dat, jejich zpracování a vizuální prezentaci. K tomu se hodí data ukládat do tabulek.
df = pd.DataFrame(index=x) # Prázdná tabulka se zadanými hodnotami řádkového indexu
df["sinus"] = np.sin(x) # vytvoření sloupce s daty
df["kosinus"] = np.cos(x) # vytvoření dalšího sloupce s daty
df
| sinus | kosinus | |
|---|---|---|
| 0.00000 | 0.000000 | 1.000000 |
| 0.10101 | 0.100838 | 0.994903 |
| 0.20202 | 0.200649 | 0.979663 |
| 0.30303 | 0.298414 | 0.954437 |
| 0.40404 | 0.393137 | 0.919480 |
| ... | ... | ... |
| 9.59596 | -0.170347 | -0.985384 |
| 9.69697 | -0.268843 | -0.963184 |
| 9.79798 | -0.364599 | -0.931165 |
| 9.89899 | -0.456637 | -0.889653 |
| 10.00000 | -0.544021 | -0.839072 |
100 rows × 2 columns
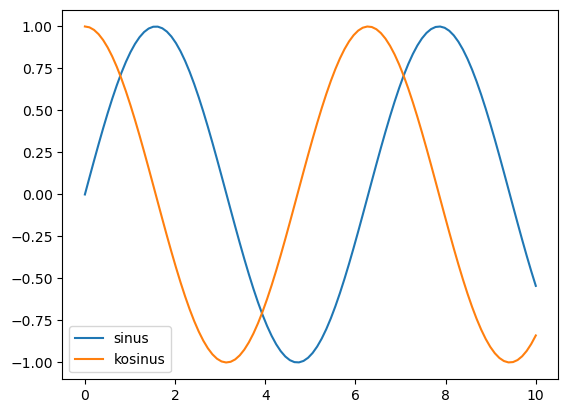
df.plot()
<Axes: >
U velkých tabulek je efektivnější a pohodlnější nejprve vytvořit tabulku i se sloupci a poté do ní doplnit data. Následující kód připraví proměnné a prázdnou tabulku.
K = 1
r_seznam = np.array([1,2,3])
x = np.linspace(0,1,100)
df = pd.DataFrame(index=x, columns=r_seznam)
df
| 1 | 2 | 3 | |
|---|---|---|---|
| 0.000000 | NaN | NaN | NaN |
| 0.010101 | NaN | NaN | NaN |
| 0.020202 | NaN | NaN | NaN |
| 0.030303 | NaN | NaN | NaN |
| 0.040404 | NaN | NaN | NaN |
| ... | ... | ... | ... |
| 0.959596 | NaN | NaN | NaN |
| 0.969697 | NaN | NaN | NaN |
| 0.979798 | NaN | NaN | NaN |
| 0.989899 | NaN | NaN | NaN |
| 1.000000 | NaN | NaN | NaN |
100 rows × 3 columns
Následující kód do tabulky doplní data. Postupuje se po sloupcích.
for r in r_seznam:
df[r] = r * x * (1 - x/K)
df
| 1 | 2 | 3 | |
|---|---|---|---|
| 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 0.010101 | 0.009999 | 0.019998 | 0.029997 |
| 0.020202 | 0.019794 | 0.039588 | 0.059382 |
| 0.030303 | 0.029385 | 0.058770 | 0.088154 |
| 0.040404 | 0.038772 | 0.077543 | 0.116315 |
| ... | ... | ... | ... |
| 0.959596 | 0.038772 | 0.077543 | 0.116315 |
| 0.969697 | 0.029385 | 0.058770 | 0.088154 |
| 0.979798 | 0.019794 | 0.039588 | 0.059382 |
| 0.989899 | 0.009999 | 0.019998 | 0.029997 |
| 1.000000 | 0.000000 | 0.000000 | 0.000000 |
100 rows × 3 columns
ax = df.plot()
ax.legend(title = "Hodnota r")
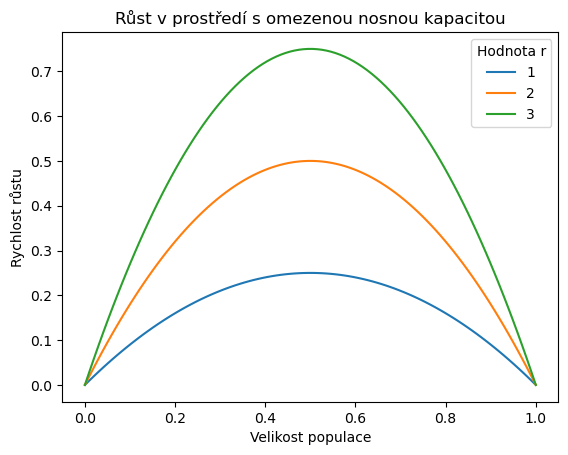
ax.set(title="Růst v prostředí s omezenou nosnou kapacitou",
xlabel="Velikost populace",
ylabel="Rychlost růstu")
[Text(0.5, 1.0, 'Růst v prostředí s omezenou nosnou kapacitou'),
Text(0.5, 0, 'Velikost populace'),
Text(0, 0.5, 'Rychlost růstu')]
1.2. Simulace ochlazování#
Následující kód vytvoří tabulku se třemi sloupci pro tři řešení. Řádkový index bude obsahovat časové údaje.
N = 500
t = np.linspace(0,5,500)
k_values = [1,2,3]
df = pd.DataFrame(index=t, columns=k_values)
T_okoli = 20
df.iloc[0,:] = 90
df
| 1 | 2 | 3 | |
|---|---|---|---|
| 0.00000 | 90 | 90 | 90 |
| 0.01002 | NaN | NaN | NaN |
| 0.02004 | NaN | NaN | NaN |
| 0.03006 | NaN | NaN | NaN |
| 0.04008 | NaN | NaN | NaN |
| ... | ... | ... | ... |
| 4.95992 | NaN | NaN | NaN |
| 4.96994 | NaN | NaN | NaN |
| 4.97996 | NaN | NaN | NaN |
| 4.98998 | NaN | NaN | NaN |
| 5.00000 | NaN | NaN | NaN |
500 rows × 3 columns
Následující kód vyřízne z tabulky sloupec s indexem 1. Ten odpovídá jednomu řešení. S tímto vektorem budeme pracovat. Protože v tomto případě nevzniká jiná proměnná, ale pouze odkaz na část tabulky, úpravou vektoru T dojde i k modifikaci dat v tabulce.
T = df[1].values
T
array([90, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan], dtype=object)
Ukázka přístupu k hodnotám. Pomocí hranaté závorky a řádkového indexu.
T[0]
90
Řádkový index jsou časové značky, ty si uložíme do proměnné t. K jednotlivým časovým značkám je možno přistupovat pomocí t[n], kde n je pořadí hodnoty ve vektoru t, číslováno od nuly.
t = df.index
t
Index([ 0.0, 0.01002004008016032, 0.02004008016032064,
0.03006012024048096, 0.04008016032064128, 0.0501002004008016,
0.06012024048096192, 0.07014028056112225, 0.08016032064128256,
0.09018036072144288,
...
4.909819639278557, 4.919839679358717, 4.929859719438878,
4.939879759519038, 4.949899799599198, 4.959919839679358,
4.969939879759519, 4.979959919839679, 4.98997995991984,
5.0],
dtype='float64', length=500)
Takto nastavíme teplotu ve druhém časovém okamžiku (tj. index času je 1, protože se indexuje od nuly) na konkrétní hodnotu.
T[1] = 50
T
array([90, 50, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan, nan,
nan, nan, nan, nan, nan], dtype=object)
Proměnná T je odkazem na stejná data, jako jsou v tabulce. Proto se automaticky změní i hodnota v tabulce.
df
| 1 | 2 | 3 | |
|---|---|---|---|
| 0.00000 | 90 | 90 | 90 |
| 0.01002 | 50 | NaN | NaN |
| 0.02004 | NaN | NaN | NaN |
| 0.03006 | NaN | NaN | NaN |
| 0.04008 | NaN | NaN | NaN |
| ... | ... | ... | ... |
| 4.95992 | NaN | NaN | NaN |
| 4.96994 | NaN | NaN | NaN |
| 4.97996 | NaN | NaN | NaN |
| 4.98998 | NaN | NaN | NaN |
| 5.00000 | NaN | NaN | NaN |
500 rows × 3 columns
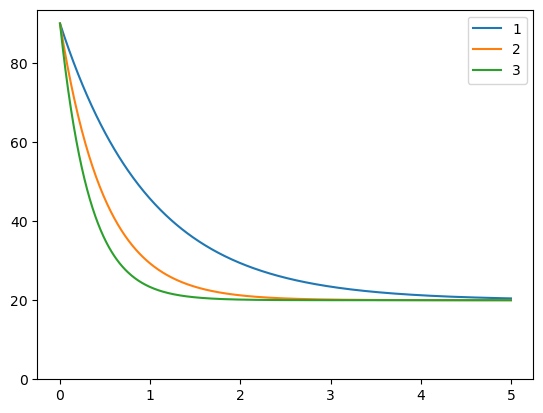
A nyní najdeme teploty v cyklu přes všechny časy a přes všechny počáteční hodnoty.
for k in k_values:
T = df[k].values
for i in range(N-1):
dt = t[i+1] - t[i]
T[i+1] = T[i] - dt*(T[i]-T_okoli)*k
ax = df.plot()
ax.set(ylim=(0,None))
[(0.0, 93.49999914938851)]
df
| 1 | 2 | 3 | |
|---|---|---|---|
| 0.00000 | 90 | 90 | 90 |
| 0.01002 | 89.298597 | 88.597194 | 87.895792 |
| 0.02004 | 88.604222 | 87.222501 | 85.854836 |
| 0.03006 | 87.916805 | 85.875357 | 83.875232 |
| 0.04008 | 87.236276 | 84.555209 | 81.955134 |
| ... | ... | ... | ... |
| 4.95992 | 20.478815 | 20.003113 | 20.000019 |
| 4.96994 | 20.474017 | 20.003051 | 20.000019 |
| 4.97996 | 20.469268 | 20.00299 | 20.000018 |
| 4.98998 | 20.464565 | 20.00293 | 20.000018 |
| 5.00000 | 20.45991 | 20.002871 | 20.000017 |
500 rows × 3 columns
Nakonec je vhodné všechny části seskupit do jedné buňky. Zpravidla totiž pojmenováváme objekty pořád stejně, aby se daly recyklovat útržky kódu (tabulka -> dataframe -> df, osy -> axes -> ax, obrázek -> figure -> fig) a takto nedojde ke kolizi mezi názvy.
N = 500
t = np.linspace(0,5,500)
k_values = [1,2,3]
T_okoli = 20
df = pd.DataFrame(index=t, columns=k_values)
df.iloc[0,:] = 90
for k in k_values:
T = df[k].values
for i in range(N-1):
dt = t[i+1] - t[i]
T[i+1] = T[i] - dt*(T[i]-T_okoli)*k
ax = df.plot()
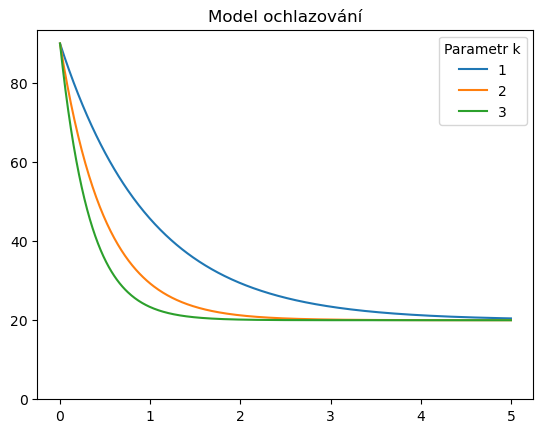
ax.set(ylim=(0,None), title="Model ochlazování")
ax.legend(title="Parametr k")
# df.to_excel("data.xlsx")
df
| 1 | 2 | 3 | |
|---|---|---|---|
| 0.00000 | 90 | 90 | 90 |
| 0.01002 | 89.298597 | 88.597194 | 87.895792 |
| 0.02004 | 88.604222 | 87.222501 | 85.854836 |
| 0.03006 | 87.916805 | 85.875357 | 83.875232 |
| 0.04008 | 87.236276 | 84.555209 | 81.955134 |
| ... | ... | ... | ... |
| 4.95992 | 20.478815 | 20.003113 | 20.000019 |
| 4.96994 | 20.474017 | 20.003051 | 20.000019 |
| 4.97996 | 20.469268 | 20.00299 | 20.000018 |
| 4.98998 | 20.464565 | 20.00293 | 20.000018 |
| 5.00000 | 20.45991 | 20.002871 | 20.000017 |
500 rows × 3 columns