5. Integrály pro pokročilé

Minivideo

Naučili jsme se integrovat pomocí neurčitého a určitého integrálu. Neurčitý integrál vyjadřuje funkční hodnotu vypočítanou z akumulace okamžitých změn. Z principiálních důvodů není možné, pokud je zadána pouze rychlost změny, určit celou veličinu, ale jenom její změnu. Proto je neurčitý integrál dán jednoznačně až na aditivní konstantu. Velikost změny na zadaném intervalu je dána určitým integrálem, ke kterému je možné dospět i geometricky a fyzikálně názorným způsobem představeným v definici Riemannova integrálu. Ten otevírá možnost rozšířit platnost mnoha fyzikálních vzorců na případ, kdy parametry úlohy nejsou konstantní. Dokážeme tak počítat dráhu pohybu proměnnou rychlostí, tlak vody na plochu ponořenou napříč různými hloubkami a podobně.

V následujícím textu rozvineme některé poznatky o integrálu, odvodíme si některé pokročilejší metody pro výpočet, ukážeme si, že každá spojitá funkce má primitivní funkci a také otevřeme cestu k definování funkcí, které nejsou elementární.

Nejprve si připomeneme jednu ze základních aplikací integrálu: nasčítání příspěvků od spojitě se měnící veličiny.

Volitelný obsah 5.1 (Příklad: proč trubky praskají podélně?)

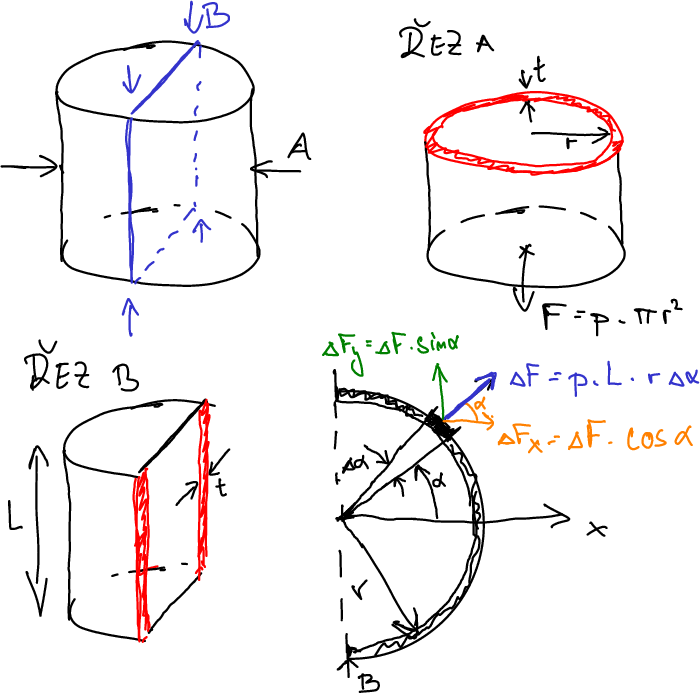
Obr. 5.1 Schema válcové nádoby pod tlakem a řezy, v nichž počítáme namáhání.

Obr. 5.2 Znalost napětí, které tlak způsobí na obalu nádoby, je důležitá pro práci s tlakovými a podtlakovými nádobami. Ty jsou nejčastěji cylindrické nebo kulové. Na obrázku unikátní zařízení pro tlakovou impregnaci ve VCJR v Útěchově se soustavou trubek a tlakových nádob. Zdroj: J. Dömény.

Obr. 5.3 Natlakovaná válcová nádoba modeluje i trubku pod tlakem. Takové trubky praskají podélně, protože v tom směru je dvojnásobné tahové napětí. Na obrázku jsou vodovodní trubky roztrhané mrazem. Zdroj: http://datagenetics.com/blog/december22013, Ian Mercer.

Uvažujme natlakovanou válcovou nádobu s tlakem \(\displaystyle p\), výškou \(\displaystyle L\), poloměrem podstavy \(\displaystyle r\) a stěnou o tloušťce \(\displaystyle t\).

Vypočteme namáhání silou v ose, tj. namáhání řezu A. Obsah řezu (vyšrafováno červeně) je \(\displaystyle 2\pi r t\). Na dno a víko působí síla \(\displaystyle F=p\pi r^2\) a v řezu A kolmém na osu válce je tahové napětí

\[\sigma_{p} = \frac FS=\frac {p\pi r^2}{2\pi rt}=\frac {pr}{2t}.\]

Směrem radiálně od osy se tlaková síla rozkládá na celou plochu pláště válce a v tomto směru je tahové napětí minimální.

Vypočteme poslední složku přispívající k namáhání pláště válce, obvodové napětí. K tomu musíme vypočítat sílu, která působí po obvodě válce, tj. která se snaží válec roztrhnout v řezu B. Tento řez má obsah (červeně vyznačeno) \(\displaystyle 2Lt\). Nejtěžší bude najít celkovou sílu, která od sebe oddaluje dvě poloviny pláště. To je místo, kde zapojíme integrál.

Kousek pláště válce odpovídající úhlu \(\displaystyle \Delta \alpha\) má obsah \(\displaystyle rL\Delta \alpha\) a tlaková síla na tento kousek je součin tlaku a obsahu, tj.

\[\Delta F=pS=p Lr\Delta \alpha .\]

Směr je kolmý k plášti válce a s vodorovnou osou svírá úhel \(\displaystyle \alpha\). Průmět této síly do vodorovného směru je

\[\Delta F_x=pLr\Delta \alpha \cos \alpha\]

a tyto příspěvky musíme posčítat na intervalu \(\displaystyle \alpha \in \left[-\frac\pi 2,\frac \pi 2\right]\). Celková síla, která se snaží nádobu roztrhnout podélně je

\[F_x=\int_{-\frac \pi2}^{\frac \pi 2} prL \cos \alpha \,\mathrm d \alpha =prL [\sin \alpha]_{-\frac \pi 2}^{\frac \pi 2}=prL \left[\sin\frac \pi 2 -\sin\left(-\frac \pi2 \right)\right]=2p rL.\]

Povrch na který tato síla působí odpovídá dvěma podélným hranám (červeně na řezu B), tj. má obsah \(\displaystyle 2Lt\) a napětí je tedy

\[\sigma_{h}=\frac{2pLr}{2Lt}=\frac{pr}t=2\sigma_p.\]

Vidíme, že toto napětí je dvojnásobkem napětí v podélné ose.

Ještě je vhodné ověřit, že svislý průmět, tj .

\[\Delta F_y=pLr\Delta \alpha \sin \alpha\]

k namáhání nepřispívá, protože

\[F_y=\int_{-\frac \pi2}^{\frac \pi 2} prL \sin \alpha \,\mathrm d \alpha =0.\]

To však je možné očekávat i ze symetrie.

Pokud se chcete dozvědět více, zkuste Google a heslo „hoop stress“.

5.1. Vlastnosti integrálu

Minivideo

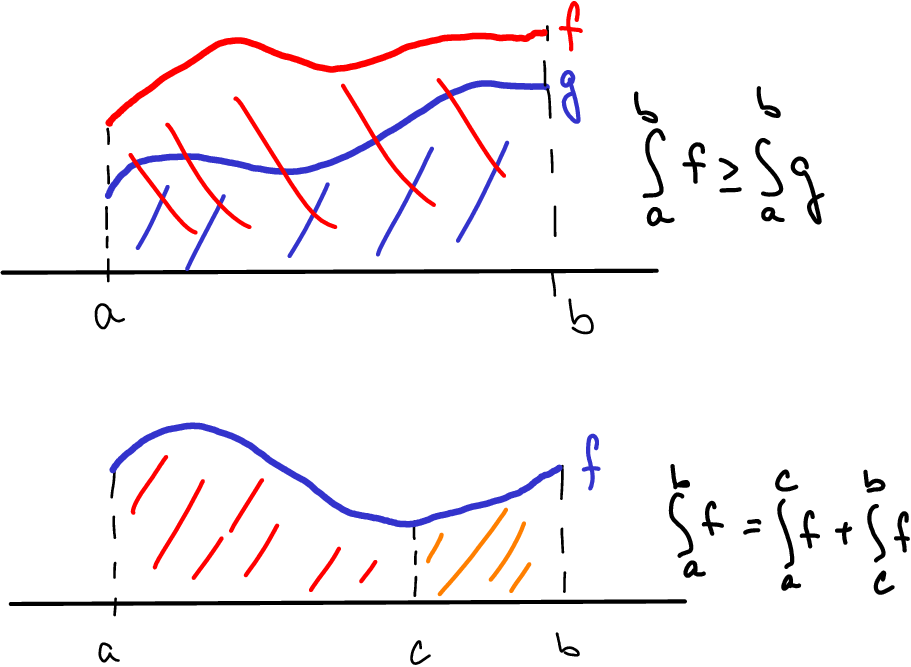
Obr. 5.4 Monotonie a aditivia vzhledem k mezi pro určitý integrál.

Z minulé přednášky víme, že integrál (určitý i neurčitý) je lineární, tj. zachovává součet funkcí a násobení konstantou.

Následující dvě věty nejsou překvapivé. Vyjadřují dvě intuitivně zřejmá fakta.

• Pokud se veličina mění rychleji, výsledná změna je větší.

• Pokud sledujeme změnu veličiny za určitý čas, můžeme sledovat změnu do nějakého mezičasu a poté od mezičasu do konce a obě částečné změny poté sečíst.

Je však důležité vědět, že tyto myšlenky platí pro libovolné integrovatelné funkce a proto zformulujeme následující věty.

Věta (Monotonie vzhledem k funkci)

Je-li \(\displaystyle f(x)\geq g(x)\) na intervalu \(\displaystyle [a,b]\), platí

\[\int_a^b f(x)\,\mathrm dx\geq \int_a^b g(x)\,\mathrm dx.\]

Věta (Integrál nezáporné funkce je nezáporný)

Integrál nezáporné funkce je nezáporný. Přesněji, je-li \(\displaystyle a<b\) a \(\displaystyle f(x)\geq 0\) na \(\displaystyle [a,b]\), platí

\[\int _a^b f(x)\,\mathrm dx \geq 0.\]

Věta (Aditivita vzhledem k integračnímu oboru)

Platí

\[\int_a^b f(x)\,\mathrm dx= \int_a^c f(x)\,\mathrm dx + \int_c^b f(x)\,\mathrm dx.\]

Věta o aditivitě vzhledem k integračnímu oboru je například pro Newtonovu definici integrálu důsledkem zřejmého vztahu

\[[F(b)-F(c)]+[F(c)-F(a)]=F(b)-F(a)\]

pro libovolnou primitivní funkci \(\displaystyle F\). Graficky i fyzikálně je názorný případ, kdy \(\displaystyle c\) leží v intervalu \(\displaystyle [a,b]\). Vzorec však platí pro libovolné uspořádání mezí podle velikosti.

5.2. Střední hodnota

Minivideo

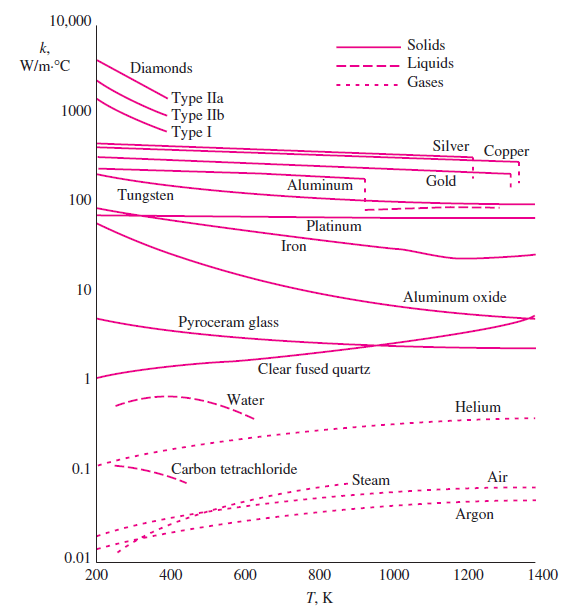
Obr. 5.5 Když materiálová konstanta není konstantní a chceme ji zprůměrovat, použijeme integrální střední hodnotu. Zdroj: Cengel, Ghajar: Heat and Mass Transfer.

Určitou souvislost s monotonií vzhledem k funkci má otázka, zda je možné funkci definovanou na intervalu \(\displaystyle [a,b]\) nahradit funkcí konstantní tak, aby obě funkce měly stejný integrál. V praxi to znamená, že bychom například při pohybu tělesa časový průběh rychlosti nahradili jednou hodnotou takovou, že dráha za daný čas bude stejná. To je přesně to, co známe z běžného života jako definici průměrné rychlosti. Je to současně i návod pro následující rozšíření pojmu průměrná rychlost na libovolné integrovatelné funkce. Jedná se vlastně o jakousi průměrnou hodnotu, při které ale nepočítáme průměr z konečného počtu hodnot, ale z hodnot rozložených spojitě na zadaném intervalu.

Definice střední hodnoty je snadným důsledkem toho, že hledáme hodnotu \(\displaystyle \mu\) s vlastností

\[\int_a^b f(x)\,\mathrm dx=\int_a^b \mu\,\mathrm dx=\mu \int_a^b \mathrm dx=\mu(b-a).\]

Definice (Střední hodnota)

Nechť \(\displaystyle f\) je funkce definovaná a integrovatelná na uzavřeném intervalu \(\displaystyle [a,b]\). Číslo \(\displaystyle \mu\) definované vztahem

\[\mu=\frac 1{b-a}\int_a^b f(x)\,\mathrm dx\]

se nazývá střední hodnota funkce \(\displaystyle f\) na intervalu \(\displaystyle [a,b]\).

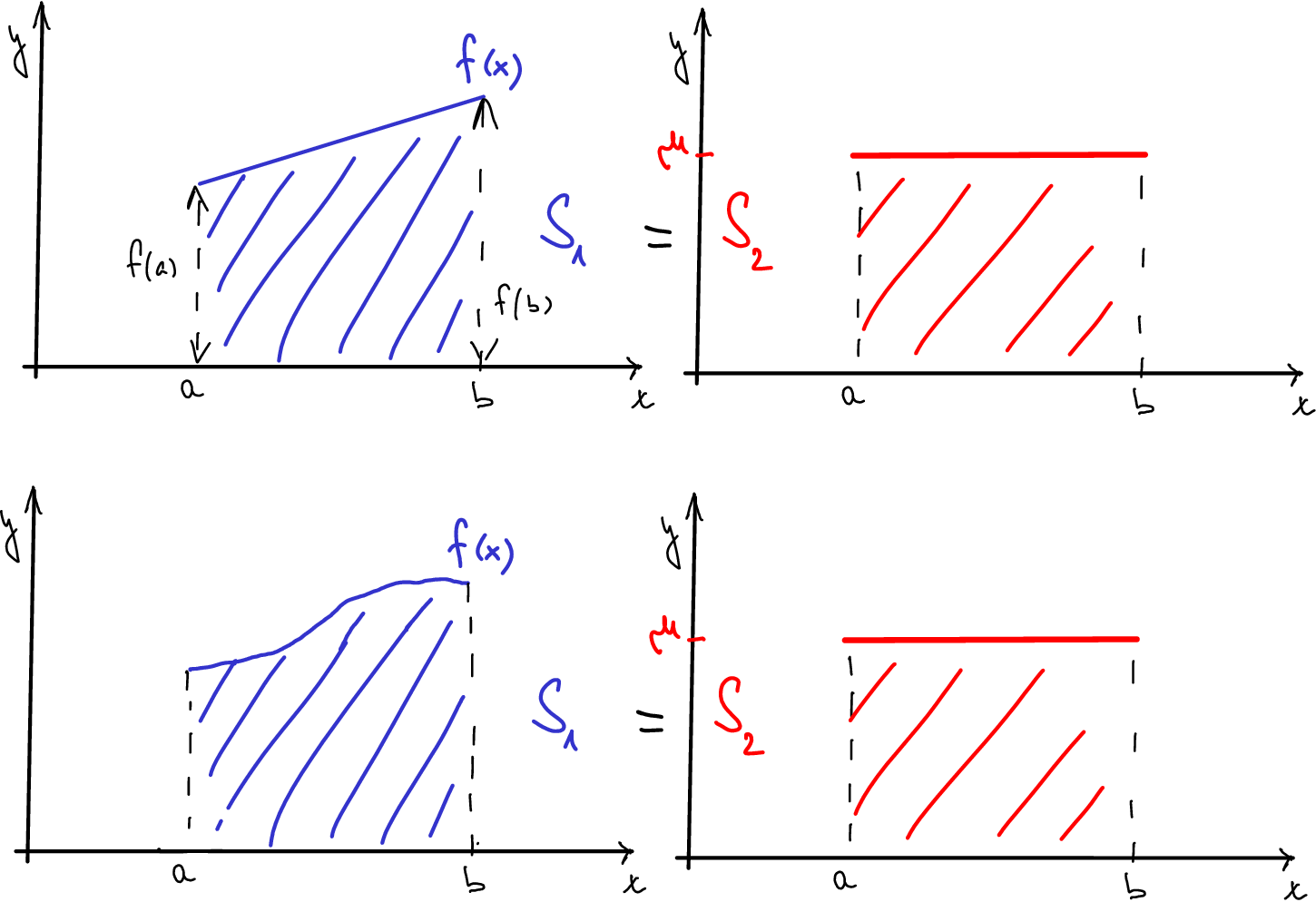
Obr. 5.6 Střední hodnota lineární a obecné funkce.

Geometricky je střední hodnota výška obdélníka, který má jednu stranu tvořenou intervalem \(\displaystyle [a,b]\) a obsah je roven integrálu \(\displaystyle \int_a^b f(x)\,\mathrm dx.\) Pokud je funkce \(\displaystyle f(x)\) kladná a lineární, je tento integrál roven obsahu lichoběžníka o základnách \(\displaystyle f(a)\) a \(\displaystyle f(b)\) a výšce \(\displaystyle b-a\). Tedy

\[\int_a^b f(x)\,\mathrm dx=(b-a)\frac{f(a)+f(b)}2\]

a střední hodnota lineární funkce je tedy průměrem hodnoty na začátku a na konci intervalu.

Poznámka (Střední hodnota materiálové konstanty)

Tepelná vodivost materiálu podobeného analýze tepelně-izolačních vlastností nemusí být konstantní v celém rozsahu teplot, ale může se měnit s teplotou. Pokud je známa funkce \(\displaystyle k(T)\), je střední hodnota tepelné vodivosti v tepelném rozsahu od \(\displaystyle T_1\) do \(\displaystyle T_2\) dána vztahem (viz Cengel, Ghajar: Heat and Mass Transfer)

\[k_{avg}=\frac 1{T_2-T_1} \int_{T_1}^{T_2} k(T)\,\mathrm dT\]

V praxi nemáme analytický předpis pro funkci \(\displaystyle k(T)\), ale funkce je dána v několika bodech tabulkou. Takové funkce můžeme integrovat numericky, což bude ukázáno v další části této přednášky.

Příklad. Střední hodnota funkce \(\displaystyle y=2x^2-1\) na intervalu \(\displaystyle [0,2]\) je

\[\frac 12 \int_0^2 2x^2-1 \,\mathrm dx=\frac 12 \left[\frac 23 x^3-x\right]_0^2=\frac 12 \left[\frac 23 8-2 - 0\right]=\frac 53.\]

Online výpočet.

Výpočet střední hodnoty si také můžete procvičit v následujících cvičeních.

Úkol Úkol Úkol

5.3. Výpočet práce pomocí integrálu

Minivideo

Volitelný obsah 5.2 (Příklad: práce při vytahování řetězu)

Obr. 5.7 Visící řetěz. Při vytahování na střechu se zmenšuje síla, kterou je nutno překonávat. Zdroj: pixabay.com

Ze střechy budovy o výšce \(\displaystyle 50\) metrů visí řetěz dlouhý \(\displaystyle 30\) metrů. Jeden metr řetězu váží dva kilogramy. Vypočítáme práci potřebnou pro povytažení řetězu o deset metrů a poté práci potřebnou pro úplné vytažení řetězu.

Z fyziky víme, že na těleso o hmotnosti \(\displaystyle m\) působí síla \(\displaystyle F\) daný vztahem

\[F=mg,\]

kde \(\displaystyle g\) je tíhové zrychlení a že práce \(\displaystyle W\) konaná silou \(\displaystyle F\) po dráze \(\displaystyle s\) je rovna součinu

\[W=Fs.\]

Pokud z budovy visí \(\displaystyle h\) metrů řetězu o lineární hustotě \(\displaystyle \tau=2\,\mathrm{kg}/\mathrm m\), je nutné při vytahování řetězu zvedat těleso o hmotnosti \(\displaystyle h\tau\), tj. vyvinout sílu

\[F=h\tau g.\]

Při vytahování řetězu se délka visící části zkracuje a změna délky \(\displaystyle \Delta h\) je záporná. Při povytažení řetězu o délku \(\displaystyle |\Delta h|=-\Delta h\) je nutné vykonat práci

\[\Delta W=F|\Delta h|=-h\tau g \Delta h.\]

Při povytažení o 10 metrů řetěz vytahujeme spojitě od \(\displaystyle h_1=30\) po \(\displaystyle h_2=20\). Celková práce je

\[\begin{split}\begin{aligned}W&=\int_{h_1}^{h_2}-h\tau g\,\mathrm dh=\tau g\int_{h_2}^{h_1}h\,\mathrm dh =\tau g\left[\frac 12 h^2\right]_{h_2}^{h_1}\\& =\tau g\left[\frac 12 h_1^2 - \frac 12 h_2^2\right]=\frac 12 \tau g (h_1^2-h_2^2) \\&=\frac 12 \tau g (h_1-h_2)(h_1+h_2). \end{aligned} \end{split}\]

Pro \(\displaystyle \tau =2\,\mathrm{kg}\,\mathrm m^{-1}\) a \(\displaystyle g=9.81\, \mathrm{kg}\,\mathrm{m}\,\mathrm {s}^{-2}\) dostáváme \(\displaystyle W=4905\,\mathrm J.\) Formálně je tento výsledek stejný, jako bychom hmotnost dolních \(\displaystyle h_1-h_2\) metrů řetězu soustředili do středu tohoto úseku (tedy do úrovně \(\displaystyle \frac 12 (h_1+h_2)\) metrů pod střechu) a poté tento hmotný bod přemístili konstantní silou po dráze \(\displaystyle \frac 12 (h_1+h_2)\) na střechu.

Práci pro vytažení celého řetězu dostaneme volbou \(\displaystyle h_2=0\). Tedy

\[W=\frac 12 \tau g h_1^2\]

a numericky \(\displaystyle W=8829\,\mathrm J.\) Protože vytáhnout první třetinu nejtěžší, očekáváme, že práce potřebná pro vytažení celého řetězu bude menší než trojnásobek práce nutné pro povytažení o třetinu. Toto se přirozeně potvrzuje porovnáním numerických hodnot.

Online výpočet.

Poznámka (Práce konaná silou proměnné velikosti)

Práce vykonaná silou \(\displaystyle F(x)\) při přemístění tělesa z polohy \(\displaystyle x=a\) do polohy \(\displaystyle x=b\) je

\[W=\int_a^b F(x)\,\mathrm dx.\]

Jako speciální případ dostáváme pro konstantní sélu \(\displaystyle F\) středoškolský vzorec

\[W=Fs,\]

kde \(\displaystyle s=b-a\) je posunutí.

Volitelný obsah 5.3 (Příklad: práce při čerpání vody)

Obr. 5.8 Mojžíšův most je z obou stran chráněný přehradou umožňující regulací výšky vody v okolí mostu, vzhledem k charakteru krajiny v Holandsku však není překvapení, že může být i zatopený. Zdroj: http://veryhungryexplorer.com/the-day-i-nearly-walked-on-water/

Pokud potřebujeme vyčerpat vodu z rezervoáru, nádrže, rybníka nebo jezera, musíme ji dopravit za stěnu (za hráz, dostat na břeh, …). Představme si, že po opadnutí vody v okolí Mojžíšova mostu, se kterým jsme se seznámili na minulé přednášce, zůstane uvnitř voda. Tu je potřeba vyčerpat. Tím se most proměnil v nádrž o hloubce \(\displaystyle H\). Povrch hladiny ve chvíli, kdy je voda \(\displaystyle x\) jednotek délky pod okrajem mostu označme \(\displaystyle S\). (Pro nádrž ve tvaru kvádru by \(\displaystyle S\) bylo konstantní a rovno obsahu dna.)

1. Pro vyzvednutí tělesa o hmotnosti \(\displaystyle m\) o výšku \(\displaystyle h\) musíme vykonat práci \(\displaystyle W=mgh,\) abychom vykompenzovali nárůst potenciální energie.

2. Vodu v nádrži rozdělíme na vodorovné vrstvy o výšce \(\displaystyle \Delta x\). Hmotnost vrstvy o výšce \(\displaystyle \Delta x\) v hloubce \(\displaystyle x\) pod okrajem nádrže bude \(\displaystyle \Delta m=S\Delta x\rho\) a abychom vodu dostali přes okraj, musíme vykonat práci

   \[\Delta W=\Delta m gx=S\Delta x\rho gx.\]

3. Celková práce na vyčerpání vody se vypočte jako součet jednotlivých příspěvků. Spojitě se měnící veličinu sčítáme integrálem, což vede na vztah

   \[W=\int_0^H S\rho gx \,\mathrm dx=\rho g\int_0^H Sx \,\mathrm dx.\]

4. Pro nádrže ve tvaru kvádru by veličina \(\displaystyle S\) byla konstantní a integrál by vycházel

   \[W=S\rho g\int_0^H x\,\mathrm dx=S\rho g\left[\frac 12 x^2\right]_0^H=S\rho g\frac 12 H^2=(SH\rho)g\frac 12 H.\]
   Výraz \(\displaystyle SH\rho\) je celková hmotnost. Práce je tedy stejná, jako kdybychom těleso o stejné hmotnosti jako je hmotnost vodní masy zvedli z poloviční hloubky pod hladinou na úroveň hladiny. Je to stejná práce, jakou bychom vykonali, kdyby všechna voda byla stlačena v těžišti a my bychom tuto vodu zvedli na úroveň okraje nádrže.

5.4. Numerická aproximace určitého integrálu

Minivideo

Následující myšlenka se si týká výlučně určitého integrálu, ale dále v dnešní přednášce si představíme nástroj, který umožní ji použít i pro integrál neurčitý.

Někdy se stane, že neumíme nebo nepotřebujeme určitý integrál vypočítat přesně. Nebo že ani nemáme dostatek informací pro přesný výpočet, například funkce může být známa jenom v několika bodech, které jsou výsledkem měření a mimo tyto body nejsou žádné informace o funkčních hodnotách. To je přesně situace pro numerickou aproximaci určitého integrálu. Mechanický model základních myšlenek aproximace je shrnut v několika následujících bodech.

• Představme si, že máme určit dráhu pohybu, ale v zadaném časovém intervalu máme pouze několik záznamů hodnoty rychlosti z tachometru.

• Mimo tyto záznamy se mohlo dít v podstatě cokoliv. Budeme však doufat, že rychlost se měnila spíše pozvolna.

• Základní taktika odhadu dráhy může být taková, že mezi každými zaznamenanými hodnotami rychlosti na tachometru nahradíme pohyb rovnoměrným pohybem rychlostí, která je průměrem krajních hodnot.

• Předchozí postup aplikovaný na libovolnou funkci odpovídá tomu, že mezi každými dvěma hodnotami nahradíme funkci funkcí lineární a poté integrál vypočítáme pro tuto lineární funkci. Tento postup (lichoběžníkové pravidlo) je možné modifikovat nebo vylepšit. Například je možné použít pro aproximaci části parabol místo přímek (Simpsonovo pravidlo). U funkce, která je rostoucí, je možné například použít funkční hodnotu v dolní mezi a tím dostaneme dolní odhad pro výsledný integrál.

Příklad. Zahradnická firma vytáhla pařez a malotraktorem jej odtáhla o 20 metrů bokem. Vzhledem k nepravidelnému tvaru a tažení po různých druzích povrchu po cestě se síla měnila. Pracovníkovi se podařilo odhadnout sílu během pohybu. Závislost síly na dráze zachycuje následující tabulka.

\(\displaystyle s\)/m	0	5	10	15	20
\(\displaystyle F\)/kN	2.3	1.5	2.1	3.1	2.0

Odhadneme celkovou vykonanou práci.

\[W=5 \frac{2.3+1.5}2 +5 \frac{1.5+2.1}2 +5 \frac{2.1+3.1}2 +5 \frac{3.1+2.0}2=44.25 \,\mathrm{kN}\,\mathrm {m} = 44.25\,\mathrm{kJ}\]

Poznámka. V předchozím příkladě byla funkce dána v pravidelných intervalech. Proto se ve všech členech objevuje faktor \(\displaystyle \frac 52\), který je možné vytknout. Po vytknutí zůstane v závorce součet, kde se hodnoty funkce v dolní a horní mezi objeví jednou a ostatní dvakrát. To v obecném případě vede k následujícímu vzorci.

Věta (Lichoběžníkové pravidlo)

Nechť je funkce \(\displaystyle f\) spojitá na intervalu \(\displaystyle [a,b]\). Rozdělme interval \(\displaystyle [a,b]\) na \(\displaystyle n\) intervalů stejné délky \(\displaystyle h\), tj. platí \(\displaystyle h=\frac{b-a}n\). Krajní body těchto intervalů označme po řadě \(\displaystyle x_0\), \(\displaystyle x_1\), …, \(\displaystyle x_n\) a jim odpovídající funkční hodnoty funkce \(\displaystyle f\) po řadě \(\displaystyle y_0\), \(\displaystyle y_1\), …, \(\displaystyle y_n\). Platí

\[ \int_a^bf(x)\,\mathrm dx\approx \frac h2\Bigl( {y_0}+2y_1+2y_2+\cdots+2y_{n-1}+{y_n}\Bigr). \]

Poznámka (Slovní interpretace lichoběžníkového pravidla)

Pokud ve vzorci pro lichoběžníkové pravidlo dosadíme za hodnotu \(\displaystyle h\) odpovídající délku intervalu \(\displaystyle \frac{ b-a}n\) a přeuspořádáme členy, dostaneme

\[ \int_a^bf(x)\,\mathrm dx\approx (b-a)\frac {{y_0}+2y_1+2y_2+\cdots+2y_{n-1}+{y_n}}{2n} \]

a

\[ \frac 1{b-a}\int_a^bf(x)\,\mathrm dx\approx \frac {{y_0}+2y_1+2y_2+\cdots+2y_{n-1}+{y_n}}{2n}. \]

Toto je odhad pro veličinu, kterou jsme výše nazvali střední hodnotou. Lichoběžníkové pravidlo je tedy možné chápat tak, že vezmeme funkční hodnoty v pravidelných intervalech a vypočteme vážený průměr těchto hodnot, kdy všechny funkční hodnoty ve vnitřních bodech se berou s dvojnásobnou vahou než funkční hodnoty v krajních bodech. To je odhad střední hodnoty, který stačí vynásobit délkou intervalu a dostaneme odhad integrálu.

Výpočet pomocí lichoběžníkového pravidla si také můžete procvičit v následujícím cvičení.

Úkol

5.5. Integrace substituční metodou

Minivideo

Substituční metoda je metoda odvozená z derivace složené funkce

\[[u(v(x))]'=u'(v(x))v'(x),\]

což dává

(5.1)\[u(v(x))=\int u'(v(x))v'(x)\,\mathrm dx.\]

Označme \(\displaystyle u'(x)=f(x)\), tj. \(\displaystyle u(x)=\int f(x)\,\mathrm dx\). Označíme-li dále \(\displaystyle v(x)=t\), platí

\[u(v(x))=u(t)=\int f(t)\,\mathrm dt.\]

Přeznačme ještě \(\displaystyle v(x)\) na \(\displaystyle \varphi(x)\). Potom má (5.1) po záměně levé a pravé strany tvar uvedený v následující větě.

Věta (Substituční metoda pro neurčitý integrál)

Platí

(5.2)\[\int f(\varphi (x))\varphi'(x)\,\mathrm dx=\int f(t)\,\mathrm dt,\]

kde po výpočtu integrálu napravo dosazujeme \(\displaystyle t=\varphi (x).\)

Formálně výraz napravo ve (5.2) přejde ve výraz nalevo a naopak dosazením rovností

\[\varphi(x)=t,\qquad \varphi'(x)\,\mathrm dx=\mathrm dt.\]

Toto je současně i návod, jak substituční metodu použít prakticky.

S použitím zápisu derivace pomocí diferenciálů máme

\[\int f(\varphi (x))\frac{\mathrm d\varphi}{\mathrm dx}\,\mathrm dx=\int f(\varphi)\,\mathrm d\varphi,\]

přičemž formálně odpadá nutnost použití proměnné \(\displaystyle t\) a vztah ukazuje, že v tomto případě je možné chápat derivaci \(\displaystyle \frac{\mathrm d\varphi}{\mathrm dx}\) jako podíl diferenciálů, s touto derivací jako s podílem diferenciálů pracovat a zkrátit člen \(\displaystyle \mathrm dx\) klasickým krácením (resp. násobením) zlomků.

Příklad. Substituce \(\displaystyle x^2=t\) vede na vztah mezi diferenciály ve tvaru \(\displaystyle 2x\,\mathrm dx=\mathrm dt\). Odsud

\[\int x e^{x^2}\,\mathrm dx=\frac 12 \int e^t\,\mathrm dt=\frac 12e^t=\frac 12 e^{x^2}+c.\]

Příklad. Substituce \(\displaystyle f(x)=t\) vede na vztah mezi diferenciály ve tvaru \(\displaystyle f'(x)\,\mathrm dx=\mathrm dt\). Odsud

\[\int \frac {f'(x)}{f(x)}\,\mathrm dx=\int \frac 1t\,\mathrm dt=\ln |t|=\ln|f(x)|+c.\]

Například

\[\int \frac{x}{x^2+1}\,\mathrm dx=\frac 12\int \frac{2x}{x^2+1}\,\mathrm dx= \frac 12\int \frac{(x^2+1)'}{x^2+1}\,\mathrm dx=\frac 12 \ln|x^2+1|+c.\]

Příklad. Substituce \(\displaystyle ax+b=t\) vede na vztah mezi diferenciály ve tvaru \(\displaystyle a\,\mathrm dx=\mathrm dt\). Odsud je možné odvodit vzorec, který již známe pro integrál funkce s lineární vnitřní složkou. Vskutku, platí

\[\int f(ax+b)\,\mathrm dx= \int \frac 1af(t)\,\mathrm dt= \frac 1a F(t)= \frac 1a F(ax+b)+C,\]

kde \(\displaystyle F(x)=\int f(x)\,\mathrm dx.\)

Vztah (5.2) je základní vztah pro substituci v neurčitém integrálu. Používáme jej ve vhodných případech zprava doleva i zleva doprava. Variantu pro určitý integrál jsme viděli ve speciálním případě ve cvičení, kdy vnitřní funkce reprezentovala konstantní násobek. Viděli jsme přirozeným způsobem, že při substituci (vyjádření v jiných jednotkách) se s integrovanou funkcí se mění i meze. Obecný vzorec pro integrování určitého integrálu substituční metodou je v následující větě.

Věta (Substituční metoda pro určitý integrál)

Platí

\[\int_a^b f(\varphi (x))\varphi'(x)\,\mathrm dx=\int_{\varphi (a)}^{\varphi(b)} f(t)\,\mathrm dt.\]

Meze tedy podléhají stejné transformaci, jako integrovaná proměnná. Pokud používáme substituci \(\displaystyle t=\varphi(x)\), potom v dolní mezi pro \(\displaystyle x=a\) platí \(\displaystyle t=\varphi(a).\) Podobná situace je i v mezi horní.

5.6. Integrál jako funkce meze

Minivideo

Integrál může být součástí definice funkce. Tím se můžeme dostat mimo množinu elementárních funkcí a značně tak rozšířit třídu funkcí, se kterými umíme pracovat.

Věta (Integrál jako funkce horní meze)

Buď \(\displaystyle f\) spojitá funkce na intervalu \(\displaystyle I\) a \(\displaystyle a\in I\). Funkce \(\displaystyle F(x)\) definovaná vztahem

\[ F(x):=\int_a^x f(t)\,\mathrm dt \]

má na intervalu \(\displaystyle I\) derivaci a platí \(\displaystyle F'(x)=f(x)\), tj. \(\displaystyle F(x)\) je primitivní funkcí k funkci \(\displaystyle f(x)\).

Příklad. Pro funkci \(\displaystyle f(x)=x^2\) platí

\[\int_0^x t^2\,\mathrm dt=\left[\frac {t^3}{3}\right]_0^{x}=\frac{x^3}{3}\]

což je skutečně jedna z primitivních funkcí k funkci \(\displaystyle x^2\), jak již víme z přednášky o neurčitém integrálu.

Věta o integrálu jako funkci horní meze dokonce udává tvar primitivní funkce pro libovolnou spojitou funkci. Tím dostáváme okamžitě následující tvrzení.

Důsledek (Postačující podmínka existence primitivní funkce)

Ke každé spojité funkci existuje neurčitý integrál.

Bohužel, ne vždy neurčitý integrál dokážeme efektivně najít. Zatímco problém nalezení derivace funkce složené z funkcí, které umíme derivovat, spočívá pouze ve správné aplikaci vzorců pro derivování, problém nalézt neurčitý integrál i k funkci tak jednoduché, jako je například \(\displaystyle e^{-x^2}\) je neřešitelný ve třídě elementárních funkcí. Totéž platí pro další „nevinně vyhlížející“ funkce jako \(\displaystyle \int \sin (x^2)\,\mathrm dx\) nebo \(\displaystyle \int \frac{\sin x}{x}\,\mathrm dx\). Věta o integrálu jako funkci horní meze nabízí možnost zapsat primitivní funkci vztahem

\[\int e^{-x^2}\,\mathrm dx=c+\int_0^x e^{-t^2}\,\mathrm dt.\]

Funkční hodnoty takové funkce můžeme určovat například tak, že integrál aproximujeme numericky.

Následující ukázka demonstruje, že i s funkcí definovanou pomocí integrálu je možné jistým způsobem pracovat, aniž bychom měli k dispozici analytické vyjádření této funkce.

Volitelný obsah 5.4 (Ukázka funkce definované pomocí integrálu)

Obr. 5.9 Součin se na součet mění například u logaritmického pravítka. Zdroj: pixabay.com

Uvažujme funkci definovanou vztahem

(5.3)\[f(x)=\int_1^x\frac 1t\,\mathrm dt.\]

Ukážeme si, že tento tvar umožňuje odvodit některé vlastnosti funkce \(\displaystyle f\). Dokážeme například, že funkce \(\displaystyle f\) mění násobení na sčítání, tj. že platí

\[f(ab)=f(a)+f(b).\]

Podle definice je

\[f(ab)=\int_1^{ab}\frac 1t \,\mathrm dt.\]

Podle aditivity vzhledem k integračnímu oboru platí

(5.4)\[f(ab)=\int_1^{a}\frac 1t \,\mathrm dt+\int_a^{ab}\frac 1t \,\mathrm dt =f(a)+\int_a^{ab}\frac 1t \,\mathrm dt.\]

Ve druhém integrálu bychom potřebovali dostat jedničku v dolní mezi, abychom dostali integrál stejný jako v definici funkce \(\displaystyle f\). Proto zavedeme substituci \(\displaystyle \frac ta=s\), \(\displaystyle t=sa\), \(\displaystyle \mathrm dt=a\mathrm ds\). S použitím této substituce se (5.4) transformuje na

\[f(ab) =f(a)+\int_1^{b}\frac 1{sa} a\,\mathrm ds =f(a)+\int_1^{b}\frac 1{s} \,\mathrm ds =f(a)+f(b).\]

Pokud si všimneme, že integrál (5.3) v definici funkce \(\displaystyle f\) je možné vypočítat a že funkce \(\displaystyle f\) je vlastně funkce \(\displaystyle \ln x\), není vlastnost, že funkce mění násobení na sčítání nijak překvapivá. Pro nás však bylo důležité, že v důkaze jsme použili jenom definici funkce \(\displaystyle f\) pomocí integrálu a pravidla pro práci s integrály. Nemuseli jsme nijak používat ani vlastnosti logaritmu, ani vlastnosti funkce k logaritmu inverzní, což bývá základem středoškolského odvození tohoto vzorce. Vidíme, že integrál je možné použít k definici funkce a s touto funkcí je možné dále pracovat. Substituce \(\displaystyle t^{\frac 1r}=s\), \(\displaystyle t=s^r\), \(\displaystyle \mathrm dt=rs^{r-1}\,\mathrm ds\) například ukáže, že platí

\[f(a^r)=\int_1^{a^r}\frac 1t\,\mathrm dt= \int _1^a \frac 1{s^r}rs^{r-1}\,\mathrm ds= r\int _1^a\frac 1s\,\mathrm ds=rf(a).\]

Volitelný obsah 5.5 (Příklad: práce při vytahování řetězu určená pomocí potenciální energie)

Obr. 5.10 Lodní výtah Falkrik Wheel. Zdroj: Wikipedie.

Vypočítáme příklad z prací při vytahování řetězu tak, že určíme změnu potenciální energie řetězu. Práci \(\displaystyle W\) vykonanou při vyzvednutí tělesa o hmotnosti \(\displaystyle m\) o výšku \(\displaystyle h\) vypočteme jako změnu potenciální energie v tíhovém poli Země, tj.

\[W=mgh.\]

Komplikace v tomto případě je, že každou část řetězu vytahujeme z jiné hloubky. Část řetězu délky \(\displaystyle \Delta h\) váží \(\displaystyle m=\tau\Delta h\) kilogramů a při vytažení z hloubky \(\displaystyle h\) na úroveň střechy je změna potenciální energie (a vykonaná práce)

\[\Delta W=mgh=\tau\Delta h g h.\]

Součet těchto příspěvků pro dolní třetinu řetězu, od \(\displaystyle h_2=20\,\mathrm m\) po \(\displaystyle h_1=30\,\mathrm m\) je

\[W=\int_{h_2}^{h_1}\tau g h\,\mathrm dh=\tau g\int_{h_2}^{h_1} h\,\mathrm dh.\]

Tím výpočet přechází ve stejný integrál jako v předchozím přístupu a výsledky jsou tedy stejné. Práci pro celý řetěz získáme opět volbou \(\displaystyle h_2=0.\)

Že práce vykonaná při vytažení celého řetězu je stejná jako změna potenciální energie celého řetězu je zřejmé. Za zmínku ještě stojí úvaha, proč je povytažení řetězu o 10 metrů ekvivalentní změně potenciální energie dolních 10 metrů při vytažení této části řetězu na střechu. Stačí uvážit, že bychom řetěz přetočili vzhůru nohama, povytáhli o 10 metrů, rozpojili a visící část znovu otočili vzhůru nohama. Otočení vzhůru nohama není spojeno s konáním práce, stejně tak rozpojení a případné opětovné napojení. Práce se tedy koná jenom tak, že řetěz vytahujeme o 10 metrů. Výsledek však je stejný, jako kdybychom řetěz nepřetáčeli, jenom odpojili dolních 10 metrů a tuto část zvedli nahoru.

Ještě možná stojí za rozvážení fakt, že při otočení řetězu okolo středu se nekoná práce. Tato skutečnost se dá opět dokázat myšlenkovým rozdělením řetězu na kousky a sečtením práce nutné pro přemístění těchto kousků. Ta bude kladná pro kousky pod těžištěm, záporná pro kousky nad těžištěm a výsledný součet bude nulový. Na podobném principu pracuje lodní výtah Falkrik Wheel. Práce potřebná pro otočení výtahu a vytažení lodě nahoru (nebo spuštění dolů nebo obojí současně) je překvapivě malá – jedna loď potenciální energii získává, druhá loď stejně velkou potenciální energii ztrácí (pokud není loď, použije se místo lodi voda) a stačí jenom vykompenzovat třecí síly v mechanismu. V minulosti zde byla soustava 11 zdymadel a lodě touto soustavou proplouvaly celý den.

5.7. Shrnutí, hlavní myšlenky

Obr. 5.11 A jaká je hlavní message? Zdroj: pixabay.com

• Naučili jsme se některé triky pro integrály: určitý integrál se dá numericky aproximovat a neurčitý integrál se dá převést metodou per-partés nebo substitucí na jiný integrál, v optimálním případě na integrál vhodný pro aplikaci vzorců.

• Integrál, resp. střední hodnota funkce, slouží jako náhrada aritmetického průměru v situacích, kdy počítáme průměr z nekonečně mnoha veličin a vzorec pro klasický aritmetický průměr selhává.

• Integrál je také nástrojem, který nás dokáže vymanit ze světa elementárních funkcí a můžeme pomocí tohoto integrálu definovat funkce, které nejsou elementární. Základním prostředkem je integrál jako funkce horní meze. Toto se využívá například ve statistice. Vedlejším produktem je věta zaručující existenci primitivní funkce pro libovolnou spojitou funkci.