8. Matice

8.1. Násobení matic

Vynásobte matice \(\displaystyle A\) a \(\displaystyle B\) pro obě pořadí násobení.

\[\begin{split}A= \begin{pmatrix} 1 & -2 & 3\\ 0 & 1 & 0\\ 1 & 2 & -2\end{pmatrix},\qquad B= \begin{pmatrix} 2 & -2 & 2\\ -1 & 2 & -1\\ 0 & 1 & 3\end{pmatrix}.\end{split}\]

Vynásobte matice \(\displaystyle B\) a \(\displaystyle C\) pro obě pořadí násobení, je-li

\[\begin{split} C= \begin{pmatrix} 1 & 0 & 0\\ 0 & 3 & 0\\ 0 & 0 & 4 \end{pmatrix}. \end{split}\]

V tomto příkladě si vyzkoušíme násobení matic a kromě toho uvidíme, že násobení diagonální maticí je v jistém smyslu jednoduché. Podle toho, v jakém pořadí násobíme matice, se diagonálními prvky se násobí řádky nebo sloupce druhé matice.

Řešení

S rozepsáním pomocí lineárních kombinací vektorů tvořených sloupci matice \(\displaystyle A\) dostáváme

\[\begin{split}2\cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} -1\cdot\begin{pmatrix} -2 \\ 1 \\ 2 \end{pmatrix} +0\cdot\begin{pmatrix}3\\ 0\\ -2\end{pmatrix} = \begin{pmatrix} 4\\ -1\\ 0\end{pmatrix}\end{split}\]

\[\begin{split}-2\cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}+2\cdot\begin{pmatrix} -2 \\ 1 \\ 2 \end{pmatrix}+1\cdot\begin{pmatrix}3\\ 0\\ -2\end{pmatrix} = \begin{pmatrix}-3\\ 2\\ 0\end{pmatrix}\end{split}\]

\[\begin{split}2\cdot \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}-1\cdot\begin{pmatrix} -2 \\ 1 \\ 2 \end{pmatrix}+3\cdot\begin{pmatrix}3\\ 0\\ -2\end{pmatrix}=\begin{pmatrix}13\\ -1\\ -6\end{pmatrix} \end{split}\]

Odsud dostáváme

\[\begin{split} AB= \begin{pmatrix} 4 & -3 & 13 \\ -1 & 2 & -1\\ 0 & 0 & -6 \end{pmatrix} \end{split}\]

Jinou metodou, s podrobným rozepsáním pomocí skalárního součinu řádků první matice a sloupců druhé matice dostáváme

\[\begin{split} \begin{aligned} AB&= \begin{pmatrix} 1 & -2 & 3\\ 0 & 1 & 0\\ 1 & 2 & -2 \end{pmatrix} \begin{pmatrix} 2 & -2 & 2\\ -1 & 2 & -1\\ 0 & 1 & 3 \end{pmatrix} \\&= \begin{pmatrix} 1\times 2-2\times (-1)+3\times 0 & 1\times (-2)-2\times 2+3\times 1 & 1\times 2-2\times (-1)+3\times 3\\ 0\times 2 +1\times (-1) +0\times 0 & 0\times (-2) +1\times 2 +0\times 1 & 0\times 2 +1\times (-1) +0\times 3 \\ 1\times 2 +2\times (-1) -2\times 0 & 1\times (-2) +2\times 2 -2\times 1 & 1\times 2 +2\times (-1) -2\times 3 \end{pmatrix} \\&= \begin{pmatrix} 4 & -3 & 13 \\ -1 & 2 & -1\\ 0 & 0 & -6 \end{pmatrix}. \end{aligned} \end{split}\]

Poté již stručněji (rozepište si sami)

\[\begin{split} BA= \begin{pmatrix} 4 & -2 & 2 \\ -2 & 2 & -1 \\ 3 & 7 & -6 \end{pmatrix}\quad BC= \begin{pmatrix} 2 & -6 & 8 \\ -1 & 6 & -4 \\ 0 & 3 & 12 \end{pmatrix} \quad CB= \begin{pmatrix} 2 & -2 & 2 \\ -3 & 6 & -3 \\ 0 & 4 & 12 \end{pmatrix}. \end{split}\]

V případě součinů s diagonální maticí se diagonálními prvky násobí odpovídající řádky nebo sloupce matice, podle toho, v jakém pořadí součin uvažujeme.

8.2. Soustava rovnic jako násobení matic

Zapište soustavu rovnic pomocí maticového násobení

\[\begin{split} \begin{aligned} 2x_1-3x_2+2x_3&{}=12\\ 2x_1+\phantom{1}x_2+\phantom{1}x_3&{}=21\\ -x_1+3x_2+\phantom{1}x_3&{}=0\\ \end{aligned} \end{split}\]

Řešení

\[\begin{split} \begin{pmatrix} 2 & -3 & 2 \\ 2 & 1 & 1 \\ -1 & 3& 1 \end{pmatrix} \begin{pmatrix} x_1\\x_2\\x_3 \end{pmatrix} = \begin{pmatrix} 12\\21\\0 \end{pmatrix} \end{split}\]

8.3. Timmyho transformace

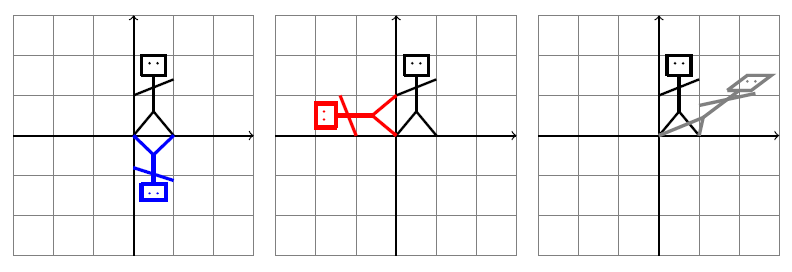
Figurka na obrázku je Timmy ve třech situacích. Jednou se pozoruje svůj obraz ve vodě, jednou spadl na záda, a jednou vrhá stín. Vyjádřete pomocí matice transformaci, která vzor (černá malůvka) převádí na obraz (barevná malůvka).

Poznámka: Stačí si všímat, kam se zobrazují jednotkové vektory ve směru os, tj. kam se zobrazí Timmiho nakročená noha a Timyho ruka, která je natažená dozadu. Případné neceločíselné složky matice jenom odhadněte. Podle LAFF Linear Algebra - Foundations to Frontiers (www.ulaff.net)

Řešení

Nakročená noha je v bodě \(\displaystyle (1,0)\) a tento bod se transformuje sám na sebe pro krajní obrázky a na bod \(\displaystyle (0,1)\) pro prostřední obrázek. Tím je dán první sloupec matice zobrazení. Ruka natažená dozadu je v bodě \(\displaystyle (0,1)\) a u modrého Timmyho se transformuje (odhadem) na \(\displaystyle (0,-0.8)\), u červeného Timmyho na \(\displaystyle (-1,0)\) a u šedého Timmyho (odhadem) na \(\displaystyle (1,0.8)\). Matice jsou postupně

\[\begin{split} M_{\text{modrá}}= \begin{pmatrix} 1 & 0 \\ 0 &-0.8 \end{pmatrix}, \quad M_{\text{červená}}= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix},\quad M_{\text{šedá}}= \begin{pmatrix} 1 & 1 \\ 0 & 0.8 \end{pmatrix}. \end{split}\]

8.4. Matice rotace

Matice rotace o úhel \(\displaystyle \theta\) v kladném smyslu je

\[\begin{split}R_\theta= \begin{pmatrix} \cos\theta & -\sin \theta\\ \sin\theta & \cos\theta \end{pmatrix}. \end{split}\]

Násobením ověřte, že matice otočení o úhel \(\displaystyle -\theta\) je k této matici inverzní.

Návod: Funkce kosinus je sudá funkce a funkce sinus je lichá funkce. Proto platí

\[\cos(-\theta)=\cos \theta \qquad\text{a}\qquad \sin(-\theta)=-\sin \theta.\]

Matice rotace je důležitá v aplikacích zabývajících se deformacemi, protože umožní odfiltrovat tu část změny polohy referenčních bodů, která je způsobena rotací a nepřispívá tedy ke změně tvaru tělesa.

Řešení

Při zkratce \(\displaystyle S=\sin \theta\) a \(\displaystyle C=\cos\theta\) platí

\[\begin{split} R_{-\theta}=\begin{pmatrix} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta) & \cos(-\theta) \end{pmatrix} =\begin{pmatrix} \cos \theta & \sin \theta \\ -\sin\theta & \cos\theta \end{pmatrix} = \begin{pmatrix} C & S\\ -S & C \end{pmatrix} \end{split}\]

a potom

\[\begin{split}R_\theta R_{-\theta}= \begin{pmatrix} C & -S \\ S& C \end{pmatrix} \begin{pmatrix} C & S\\ -S & C \end{pmatrix} = \begin{pmatrix} C^2+S^2 & CS-SC \\ SC-CS & S^2+C^2\end{pmatrix} = \begin{pmatrix} 1 & 0 \\0& 1\end{pmatrix}, \end{split}\]

kde jsme využili identitu

\[\sin^2\theta + \cos^2\theta=1.\]

8.5. Matice posunutí

Transformace pomocí násobení matic zachovává počátek a nemůže proto charakterizovat například posunutí roviny. Pokud chceme mít pomocí maticového násobení realizováno i posunutí, musíme zavést homogenní souřadnice a ztotožnit bod \(\displaystyle (x,y)\) s vektorem \(\displaystyle (x,y,1)^T\). Ukažte, že matice

\[\begin{split}P_{a,b}= \begin{pmatrix} 1& 0& a\\ 0 & 1 & b\\ 0& 0& 1 \end{pmatrix} \end{split}\]

je matice posunutí o \(\displaystyle a\) doprava a \(\displaystyle b\) nahoru. Odhadněte, jak bude vypadat matice popisující opačnou transformaci a pro jedno nějaké pořadí součinu ověřte, že součin těchto matic je jednotková matice.

Řešení

Platí

\[\begin{split} \begin{pmatrix} 1& 0& a\\ 0 & 1 & b\\ 0& 0& 1\end{pmatrix}\begin{pmatrix} x\\y\\1\end{pmatrix} = \begin{pmatrix} x+a\\y+b\\1\end{pmatrix} \end{split}\]

a vidíme, že k souřadnici \(\displaystyle x\) se přičítá \(\displaystyle a\) a k souřadnici \(\displaystyle y\) se přičítá \(\displaystyle b\). Inverzní zobrazení bude posunutí o \(\displaystyle a\) doleva a o \(\displaystyle b\) dolů, tj.

\[\begin{split} \begin{pmatrix} 1& 0& -a\\ 0 & 1 & -b\\ 0& 0& 1\end{pmatrix}.\end{split}\]

Přímým výpočtem vidíme, že platí

\[\begin{split} \begin{pmatrix} 1& 0& a\\ 0 & 1 & b\\ 0& 0& 1\end{pmatrix} \begin{pmatrix} 1& 0& -a\\ 0 & 1 & -b\\ 0& 0& 1\end{pmatrix}= \begin{pmatrix} 1& 0& 0\\ 0 & 1 & 0\\ 0& 0& 1\end{pmatrix}.\end{split}\]

8.6. Matice, zachovávající význačné směry

Dřevo má tři výrazné směry a pokud máme možnost zvolit souřadnou soustavu tak, aby tyto směry byly dány vektory \(\displaystyle (1,0,0)^T\), \(\displaystyle (0,1,0)^T\) a \(\displaystyle (0,0,1)^T\), formulace fyzikálních zákonů se zjednoduší. Nyní si ukážeme proč. Najděte

1. nejobecnější matici \(\displaystyle 3\times 3\), která zachovává směr vektoru \(\displaystyle (1,0,0)^T\),

2. nejobecnější symetrickou matici \(\displaystyle 3\times 3\), která zachovává směr vektoru \(\displaystyle (1,0,0)^T\),

3. nejobecnější symetrickou matici \(\displaystyle 3\times 3\), která zachovává směr vektorů \(\displaystyle (1,0,0)^T\), \(\displaystyle (0,1,0)^T\), \(\displaystyle (0,0,1)^T\).

V tomto příkladě uvidíme, že matice zachovávající směr os souřadnic jsou v určitém smyslu pěkné.

Řešení

ad 1.

\[\begin{split} \begin{pmatrix} a & b & c \\ d & e & f \\ g& h& i \end{pmatrix} \begin{pmatrix} 1\\0\\0 \end{pmatrix} = \begin{pmatrix} a \\ d \\g \end{pmatrix}\end{split}\]

a vektory \(\displaystyle (1,0,0)^T\) a \(\displaystyle (a,d,g)^T\) musí mít stejný směr. Proto \(\displaystyle d=g=0\) a nejobecnější matice s danou vlastností je matice, která ve druhém a třetím řádku začíná nulou.

\[\begin{split} \begin{pmatrix} a & b & c \\ 0 & e & f \\ 0& h& i \end{pmatrix}\end{split}\]

ad 2. Jako minulý případ, ale aby byla matice symetrická, musí být také \(\displaystyle b=c=0\), a \(\displaystyle h=f\) tj.

\[\begin{split} \begin{pmatrix} a & 0 & 0 \\ 0 & e & f \\ 0& f& i \end{pmatrix}.\end{split}\]

ad 3. Jako minulý případ, ale ještě se musí zachovávat směry vektorů \(\displaystyle (0,1,0)^T\) a \(\displaystyle (0,0,1)^T\). Platí

\[\begin{split} \begin{pmatrix} a & 0 & 0 \\ 0 & e & f \\ 0& f& i \end{pmatrix} \begin{pmatrix} 0 \\1\\0 \end{pmatrix} = \begin{pmatrix} 0 \\ e\\f \end{pmatrix},\quad \begin{pmatrix} a & 0 & 0 \\ 0 & e & f \\ 0& f& i \end{pmatrix} \begin{pmatrix} 0 \\0\\1 \end{pmatrix} = \begin{pmatrix} 0 \\ f\\i \end{pmatrix}\end{split}\]

a aby vzor a obraz měly stejný směr, musí být \(\displaystyle f=0\). Nejobecnější symetrická matice, která zachovává směr všech tří základních bázových vektorů je matice, která má mimo hlavní diagonálu nuly.

8.7. Matice derivování

Ukažte, že matice \(\displaystyle A=\begin{pmatrix} 0 & 0 & 0 \\ 2 & 0 & 0 \\ 0 & 1 & 0\end{pmatrix}\) je matice derivování polynomů stupně nejvýše \(\displaystyle 2\), pokud polynom \(\displaystyle ax^2+bx+c\) ztotožníme s vektorem \(\displaystyle \begin{pmatrix} a \\ b\\c\end{pmatrix}\). Vysvětlete, jak bychom interpretovali matici \(\displaystyle A^2\) a \(\displaystyle A^3\) a tyto matice vypočtěte.

Návod: je možné ukázat buď pro obecný polynom \(\displaystyle ax^2+bx+c\), nebo samostatně pro polynomy \(\displaystyle x^2\), \(\displaystyle x\) a \(\displaystyle 1\) a poté si všimnout, že ostatní polynomy můžeme dostat lineárními kombinacemi a maticová násobení tyto l ineární kombinace nepokazí díky tomu, že je distributivní a komutuje při násobení s konstantou. V tomto příkladě mimo jiné vidíme, že mocnina nenulové matice může být nula. To je efekt, který nemá obdobu u násobení reálných čísel.

Řešení

Polynom \(\displaystyle x^2\) má derivaci \(\displaystyle 2x\), tj. v označení pomocí vektorů se musí vektor \(\displaystyle (1,0,0)^T\) zobrazit na \(\displaystyle (0,2,0)^T\). Toto snadno ukážeme, že platí, protože se vlastně jedná o první sloupec matice \(\displaystyle A\). Podobně, polynom \(\displaystyle x\) má derivaci \(\displaystyle 1\) a polynom \(\displaystyle 1\) má derivaci \(\displaystyle 0\), tj. v označení pomocí vektorů se musí vektory \(\displaystyle (0,1,0)^T\) a \(\displaystyle (0,0,1)^T\) zobrazit na \(\displaystyle (0,0,1)^T\) a \(\displaystyle (0,0,0)^T\). Opět vidíme snadno, že pro naši matici \(\displaystyle A\) platí (dostáváme vlastně druhý a třetí sloupec matice \(\displaystyle A\)).

Protože libovolný polynom druhého stupně dostaneme pomocí lineárních kombinací výše uvedených vektorů a protože tyto lineární kombinace zůstanou při maticovém násobení zachovány, je při výše definovaném zobrazení obrazem libovolného polynomu druhého stupně jeho derivace.

Pro obecný polynom \(\displaystyle ax^2+bx+c\) s derivací \(\displaystyle 2ax+b\) vidíme, že obrazem vektoru \(\displaystyle (a,b,c)^T\) musí být \(\displaystyle (0,2a, b)^T\), což matice \(\displaystyle A\) opět (po krátkém výpočtu) splňuje.

Matice \(\displaystyle A^2\) je druhá derivace a \(\displaystyle A^3\) třetí derivace a mají tvar

\[\begin{split} A^2= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 2 & 0 & 0\end{pmatrix}, \qquad A^3= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}.\end{split}\]

8.8. Matice projekce (volitelný obsah)

Matice \(\displaystyle P=\begin{pmatrix} \cos^2 \alpha & \cos \alpha \sin \alpha \\ \cos\alpha\sin\alpha & \sin^2 \alpha\end{pmatrix}\) reprezentuje kolmou projekci na přímku, která jde počátkem soustavy souřadnic a svírá s kladnou částí osy \(\displaystyle x\) úhel \(\displaystyle \alpha\).

1. Ukažte, že platí \(\displaystyle P^2=P\).

2. Ukažte, (nemusíte výpočtem, například graficky, nebo využitím toho, že každý bod přímky se zobrazí sám na sebe) že dva různé body se projekcí mohou zobrazit na stejný bod a proto není naděje na to mít inverzní zobrazení. Proto neexistuje inverzní matice.

Řešení

Pro \(\displaystyle C=\cos \alpha\) a \(\displaystyle S=\sin\alpha\) dostáváme

\[\begin{split} \begin{aligned}P^2&= \begin{pmatrix} C^2 & CS \\CS & S^2 \end{pmatrix} \begin{pmatrix} C^2 & CS \\CS & S^2 \end{pmatrix} = \begin{pmatrix} C^4+C^2S^2 & C^3S+CS^3 \\C^3S+CS^3 & C^2S^2+S^4\end{pmatrix} \\&= \begin{pmatrix} C^2(C^2+S^2) & CS(C^2+S^2) \\CS(C^2+S^2) & S^2(C^2+S^2) \end{pmatrix} = \begin{pmatrix} C^2 & CS \\CS & S^2\end{pmatrix} =P\end{aligned}\end{split}\]

Evidentně jakýkoliv bod mimo přímku projekce a jeho obraz jsou dva různé body, které mají stejný obraz. Proto nemůže existovat inverzní zobrazení.

Pro determinant platí

\[\begin{split} |P|= \begin{vmatrix} C^2 & CS \\CS & S^2 \end{vmatrix} =C^2S^2-(CS)(CS)=C^2S^2-C^2S^2=0\end{split}\]

a tento výpočet potvrzuje, že neexistuje inverzní matice.