4. Integrál, integrál a integrál

Minivideo

Naučili jsme se pracovat s derivacemi, tedy s rychlostí změny. Známe-li funkci a zderivujeme ji, dostaneme rychlost změny. Pokud potom původní funkci „ztratíme“ a zůstane nám jenom derivace, je otázka, jestli dokážeme původní funkci z této derivace najít. Odpověď je zní, že v jistém smyslu ano. Spojení „v jistém smyslu“ naznačuje, že souvislost nebude tak snadná jako je souvislost u navzájem inverzních funkcí. Derivováním totiž můžeme ztratit aditivní konstanty, které v derivaci dávají nulu a zpětně není možné rekonstruovat, derivováním jaké konstanty jsme tuto nulu dostali. A protože problém uchopíme poněkud obecněji, uvedeme si dokonce hned tři různé „protijedy“ na derivování.

Jeden představíme jako opak derivace (neurčitý integrál), druhý jako změnu funkce vypočtenou ze zadané rychlosti změny (Newtonův určitý integrál) a třetí jako náhradu součtu pro případ, kdy potřebujeme sčítat nekonečně mnoho příspěvků, z nichž každý má v podstatě nulovou hodnotu (Riemannův určitý integrál).

Intervalem \(\displaystyle I\) budeme rozumět otevřený interval.

Motivace: Jak z rychlosti změny vypočítat změnu?

Derivace umožní z veličiny v prvním sloupci získat veličinu v pravém sloupci. Pohledem na tyto příklady věříme, že bude fungovat i něco, co naopak z rychlosti zrekonstruuje původní veličinu, která se touto rychlostí mění.

Závislá proměnná	Derivace podle času
veličina \(\displaystyle x\)	rychlost růstu veličiny \(\displaystyle x\)
výška stromu	rychlost růstu do výšky
objem kmene stromu (smrk)	rychlost růstu ve smyslu přírůstu dřevní hmoty
dráha	rychlost
rychlost	zrychlení
všeobecná cenová hladina (cca náklady na živobytí)	inflace

Volitelný obsah 4.1 (Ukázka úlohy vedoucí na problém nalézt funkci, mající známou derivaci.)

Motivace: Jak z derivace křivky získat rovnici křivky?

Obr. 4.1 Zavěšený most na Hauraki Rail Trail (Nový Zéland). Tyto traily byly otevřeny v květnu 2012 a získaly Winer Timber Design Award v kategorii Sustainability Zdroj: nzwood.co.nz

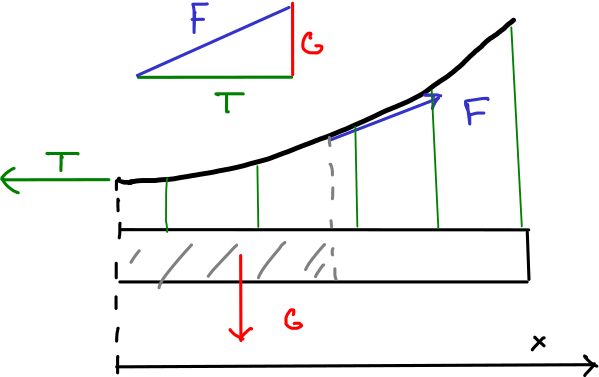
Obr. 4.2 Schema poloviny mostu se silamu působícími na část lana.

Na této úloze si připomeneme další roli derivace (směrnice tečny) a představíme si úžasný druh mostů – mosty zavěšené na nosných lanech, které mohou překlenout obrovské vzdálenosti.

U zavěšeného mostu lano nese prostřednictvím svislých lan hmotnost rovnoměrně rozloženou ve vodorovném směru. Je potřeba zvolit vhodnou délku svislých lan tak, aby síla působící na nosné lano byla vždy ve směru tohoto nosného lana. Potom je systém nejstabilnější a nejpevnější.

Díky symetrii stačí uvažovat jenom půlku mostu. Na část lana nad intervalem \(\displaystyle [0,x]\) působí následující síly.

• Tahová síla lana v minimu (\(\displaystyle x=0\)) o velikosti \(\displaystyle T\) doleva.

• Gravitační síla o velikosti \(\displaystyle G=\mu x g\) směrem dolů, kde \(\displaystyle \mu\) je lineární hustota (hmotnost jednotkové délky mostu) a \(\displaystyle \mu x\) je hmotnost části mostu, odpovídající intervalu \(\displaystyle [0,x]\).

• Tahová síla \(\displaystyle F\) doprava nahoru na pravém konci. Protože je most v klidu, velikost a směr této síly jsou takové, aby součet všech sil působících na uvažovanou část mostu byl roven nule. Jako stavitelé mostu chceme, aby směr síly souhlasil se směrem lana, tj. aby síla byla tečná k nosnému lanu.

Vektorový součet sil musí být nulový a proto všechny tři síly tvoří pravoúhlý trojúhelník. Poměr odvěsen \(\displaystyle \frac{\mu g x}{T}\) udává směrnici přepony. Křivka udávající směr nosného lana tedy musí mít tvar funkce, která splňuje

\[y'=\frac{\mu g}{T} x,\]

kde \(\displaystyle \mu\), \(\displaystyle g\), a \(\displaystyle T\) jsou pro danou úlohu konstanty.

---

Z rozboru vidíme, že máme dánu křivku danou pomocí derivace a tuto křivku musíme najít. Formálně to je stejný problém, jako když máme rychlost změny funkce a chceme najít časový průběh této funkce. Mechanickým modelem může být například pohyb zadanou rychlostí a úloha určit dráhu tohoto pohybu. Tento problém se na základní škole redukuje na případ pohybu konstantní rychlostí (\(\displaystyle s=vt\)) a na střední škole rozšiřuje na rychlost, která se mění jako lineární funkce (\(\displaystyle s=\frac 12 at^2\)). Nyní stojíme před úkolem, jak si poradit v případě obecné rychlosti, měnící se libovolně. Přesně to je úkol pro neurčitý integrál.

4.1. Neurčitý integrál

Minivideo

Představíme nástroj, který nám umožní odpovědět na následující otázky.

• Je znám směr křivky v každém bodě (tj. směr tečny, derivace). Jaká je rovnice křivky?

• Je známa rychlost, s jakou se mění veličina \(\displaystyle f\). Jaká je rovnice udávající závislost veličiny \(\displaystyle f\) na čase?

Definice (Neurčitý integrál)

Řekneme, že funkce \(\displaystyle F\) je primitivní funkcí k funkci \(\displaystyle f\) na intervalu \(\displaystyle I\), jestliže platí

\[F'(x)=f(x)\]

na intervalu \(\displaystyle I\). Množina všech primitivních funkcí k funkci \(\displaystyle f\) se nazývá neurčitý integrál funkce \(\displaystyle f\) a značí

\[\int f(x)\,\mathrm dx.\]

Otázkou existence primitivní funkce se budeme zabývat na další přednášce. Otázku (ne-)jednoznačnosti řeší následující věta.

Věta (Jednoznačnost primitivní funkce)

Primitivní funkce je dána jednoznačně, až na aditivní konstantu.

• Je-li \(\displaystyle F\) primitivní funkcí k funkci \(\displaystyle f\) na intervalu \(\displaystyle I\), platí totéž i pro funkci \(\displaystyle G(x)=F(x)+c\), kde \(\displaystyle c\in\mathbb R\).

• Jsou-li \(\displaystyle F\) a \(\displaystyle G\) primitivní funkce k téže funkci \(\displaystyle f\) na intervalu \(\displaystyle I\), existuje \(\displaystyle c\in\mathbb R\) takové, že

  \[ F(x)=G(x)+c \]
  na \(\displaystyle I\).

Příklad. Funkce \(\displaystyle x^2\) má primitivní funkce například \(\displaystyle \frac 13 x^3\), nebo \(\displaystyle \frac 13 x^3+7\), nebo \(\displaystyle \frac 13 x^3+\pi\), protože derivace všech těchto tří funkcí je \(\displaystyle x^2\). Platí

\[\int x^2 \,\mathrm dx=\frac 13 x^3+c,\qquad c\in\mathbb R.\]

Poznámka 4.1 (Vzorce pro výpočet integrálu)

Následující vzorce jsou zpravidla vzorce pro derivování napsané naopak (integrál derivace je roven původní funkci, až na aditivní konstantu).

1. \(\displaystyle \displaystyle\int c\,\mathrm dx=cx+C\)

2. \(\displaystyle \displaystyle\int x^n\,\mathrm dx= \frac{x^{n+1}}{n+1}+C\)

3. \(\displaystyle \displaystyle\int \frac 1x\,\mathrm dx=\ln |x|+C\)

4. \(\displaystyle \displaystyle\int e^x\,\mathrm dx=e^x+C\)

5. \(\displaystyle \displaystyle\int \sin x\,\mathrm dx=-\cos x+C\)

6. \(\displaystyle \displaystyle\int \cos x\,\mathrm dx=\sin x+C\)

7. \(\displaystyle \displaystyle\int \frac 1{\cos^2 x}\,\mathrm dx=\mathop{\mathrm{tg}} x+C\)

8. \(\displaystyle \displaystyle\int \frac 1{\sin^2 x}\,\mathrm dx=-\mathop{\mathrm{cotg}} x+C\)

9. \(\displaystyle \displaystyle\int \frac 1{A^2+x^2}\,\mathrm dx=\frac 1A \mathrm{\mathrm {arctg}} \frac xA+C\)

10. \(\displaystyle \displaystyle\int \frac1{\sqrt{A^2-x^2}}\,\mathrm dx=\arcsin\frac xA+C\)

11. \(\displaystyle \displaystyle\int f(ax+b)\,\mathrm dx=\frac 1a F(ax+b)+C\), kde \(\displaystyle F(x)=\int f(x)\,\mathrm dx\)

Věta (Linearita neurčitého integrálu)

Neurčitý integrál zachovává součet a násobení konstantou. Tedy pro libovolné funkce \(\displaystyle f\), \(\displaystyle g\) a libovolnou konstantu \(\displaystyle c\) platí

\[\begin{split} \begin{aligned} \int f+g\,\mathrm dx&=\int f\,\mathrm dx + \int g\,\mathrm dx,\\ \int cf\,\mathrm dx&=c\int f\,\mathrm dx. \end{aligned} \end{split}\]

Příklad.

\[\int 2x^4-e^{4x}+\frac 1x\,\mathrm dx=\frac 25 x^5 -\frac 14 e^{4x}+\ln |x|+C\]

Integrování si také můžete procvičit v následujících cvičeních.

Úkol Úkol Úkol Úkol Úkol Úkol

4.1.1. Funkční předpis z rychlosti změny a výchozího stavu

Obr. 4.3 Napětí na kondenzátoru při měření elektrického odporu RC členem se mění exponenciální rychlostí. Úloha najít vývoj napětí v čase je formálně stejná, jako tato úloha s exponenciálně klesající teplotou. Zdroj: https://www.handymantips.org/

Uvažujme těleso, jehož teplota klesá známou rychlostí. Derivace teploty podle času je \(\displaystyle \frac{\mathrm dT}{\mathrm dt}=-0.1 e^{-0.01 t} \,{}^\circ \mathrm C/\mathrm{min}.\) Cílem je najít teplotu jako funkci času. Dodatečná informace je, že počáteční teplota je \(\displaystyle 28 ^\circ \mathrm{C}\).

Použijeme skutečnost, že integrál konstantního násobku je konstantní násobek integrálu a vzorec

\[\int e^{ax}\,\mathrm{d}x=\frac 1a e^{ax}+c.\]

Teplota jako funkce času je dána integrálem

\[T=\int - 0.1 e^{-0.01t} \,\mathrm dt=\frac{-0.1}{-0.01} e^{-0.01t}+C = 10 e^{-0.01t}+C.\]

Hodnota \(\displaystyle C\) souvisí s počáteční teplotou. Protože počáteční teplota je \(\displaystyle 28 ^\circ \mathrm{C}\), dosadíme do vztahu pro \(\displaystyle T\) hodnoty \(\displaystyle T=28 ^\circ \mathrm{C}\) a \(\displaystyle t=0\) a ze vzniklé rovnice určíme \(\displaystyle C\). Dostáváme takto podmínku

\[28=10 e^0 +C,\]

která implikuje \(\displaystyle C=18 ^\circ \mathrm C\). Funkce udávající závislost teploty místnosti na čase je

\[T=\left(18+10 e^{-0.01 t}\right)\,{}^\circ \mathrm C.\]

Online výpočet (Python)

Online výpočet (Sage)

Poznámka (vlhkost dřeva elektrickou metodou). Podobný výpočet se využívá u měření elektrického odporu dřeva pro stanovení vlhkosti. Protože elektrický odpor dřeva je velký, není vhodné pro určení elektrického odporu použít Ohmův zákon a změřený proud a napětí. Jedna z možností je měření času nutného k nabití nebo vybití kondenzátoru přes odpor. V případě nabíjení proud exponenciálně klesá (zdůvodníme později v přednášce věnované diferenciálním rovnicím) a proto (díky elektrickým vlastnostem kondenzátoru) exponenciálně klesá i rychlost, s jakou roste napětí na kondenzátoru. Toto napětí je nutné pro výpočet odporu. Pokud známe rychlost, s jakou se napětí mění, určíme napětí integrováním a znalostí napětí na začátku nabíjení.

Poznámka (Veličina vypočtená z rychlosti své změny)

Pokud se veličina \(\displaystyle f(t)\) mění v čase rychlostí \(\displaystyle r(t)\), platí

\[f(t)=\int r(t)\,\mathrm dt,\]

přičemž pravá strana je dána jednoznačně až na aditivní konstantu. To koresponduje s pozorováním, že rychlost změn k jednoznačné identifikaci časového průběhu měnící se veličiny nestačí. Je potřeba mít zadán ještě výchozí stav.

Příklad. V úvodu přednášky je popsáno, že křivka, která je přirozená pro nosné lano zavěšeného mostu, splňuje rovnici

\[y'=\frac{\mu g}{T}x.\]

Pouze za této podmínky bude lano namáháno ve směru své nejvyšší pevnosti, tj. v podélném směru, ve směru své osy. Integrací získáme

\[y=\int \frac{\mu g}{T}x\,\mathrm dx=\frac{\mu g}{2T }x^2+C.\]

Lano tedy bude v každém bodě namáháno ve směru své osy pokud má tvar paraboly. Prohnutí paraboly (koeficient u \(\displaystyle x^2\)) je dáno hmotností mostu a tahem napínajícím lano.

4.2. Určitý integrál (Newtonův)

Minivideo

Představíme si mírnou modifikaci neurčitého integrálu. Rychlost změny nebudeme používat k hledání předpisu funkce, ale budeme hledat změnu funkce na zadaném intervalu.

Definice (Newtonův určitý integrál)

Buď \(\displaystyle f\) funkce a \(\displaystyle F\) její primitivní funkce na intervalu \(\displaystyle I\). Buď \(\displaystyle [a,b]\subset I\) podinterval v \(\displaystyle I\). Určitým integrálem funkce \(\displaystyle f\) na intervalu \(\displaystyle [a,b]\) rozumíme veličinu označenou a definovanou vztahem

\[\int_a^b f(x)\mathrm dx:=F(b)-F(a).\]

Označení. Výraz \(\displaystyle F(b)-F(a)\), tj. změnu funkce \(\displaystyle F(x)\) na intervalu \(\displaystyle [a,b]\), označujeme také \(\displaystyle [F(x)]_a^b\). Tento zápis se často používá jako mezivýpočet při výpočtu určitého integrálu.

\[\int_0^1 x^2 \,\mathrm dx=\left[\frac 13 x^3\right]_0^1=\frac 13 (1)^3 -\frac 13 (0)^3=\frac 13\]

Věta (Linearita určitého integrálu)

Určitý integrál zachovává součet a násobení konstantou. Tedy pro libovolné funkce \(\displaystyle f\), \(\displaystyle g\) a libovolnou konstantu \(\displaystyle c\) platí

\[\begin{split} \begin{aligned} \int_a^b f+g\,\mathrm dx&=\int_a^b f\,\mathrm dx + \int_a^b g\,\mathrm dx,\\ \int_a^b cf\,\mathrm dx&=c\int_a^b f\,\mathrm dx. \end{aligned} \end{split}\]

Snadným důsledkem definice určitého integrálu je následující věta.

Věta (Záměna mezí a rovnost mezí v určitém integrálu)

Platí

\[\begin{split} \begin{aligned} \int _a^a f(x)\,\mathrm dx&=0,\\ \int _a^b f(x)\,\mathrm dx&=- \int _b^a f(x)\,\mathrm dx. \end{aligned} \end{split}\]

4.2.1. Změna funkce z rychlosti změny (časová změna teploty)

Uvažujme těleso, jehož teplota klesá známou rychlostí. Derivace teploty podle času je \(\displaystyle \frac{\mathrm dT}{\mathrm dt}=-0.1 e^{-0.01 t} \,{}^\circ \mathrm C/\mathrm{min}.\) Chceme určit pokles teploty za první hodinu a pokles teploty za druhou hodinu.

Neurčitý integrál

\[\int - 0.1 e^{-0.01t} \,\mathrm dt=10 e^{-0.01t}+C\]

jsme vypočítali v podkapitole s neurčitým integrálem. Potřebovali jsme ještě znát počáteční hodnotu teploty a našli jsme teplotu jako funkci času.

Nyní zapojíme určitý integrál. Nepotřebujeme informaci o počáteční teplotě, ale zato jsme schopni určit jenom změnu teploty za daný časový interval. Za první hodinu bude změna teploty

\[\int_0^{60} - 0.1 e^{-0.01t} \,\mathrm dt=\left[10 e^{-0.01t}\right]_0^{60}= 10 e^{-0.01\cdot 60} - 10 e^{-0.01\cdot 0}\approx -4.5 ^\circ \mathrm C.\]

Za druhou hodinu bude změna teploty

\[\int_{60}^{120} - 0.1 e^{-0.01t} \,\mathrm dt=\left[10 e^{-0.01t}\right]_{60}^{120}= 10 e^{-0.01\cdot 120} - 10 e^{-0.01\cdot 60}\approx -2.5 ^\circ \mathrm C. \]

Online výpočet (Python)

Online výpočet (Sage).

Integrování určitým integrálem si také můžete procvičit v následujících cvičeních.

Úkol Úkol Úkol

Poznámka (Změna veličiny vypočtená pomocí rychlosti)

Pokud se veličina \(\displaystyle f(t)\) mění v časovém intervalu od \(\displaystyle t=a\) do \(\displaystyle t=b\) rychlostí \(\displaystyle r(t)\), je změna veličiny \(\displaystyle f\) za tento časový okamžik rovna

\[\Delta f=f(b)-f(a)=\int_a^b r(t)\,\mathrm dt.\]

Slovní úlohy kde se hledaná veličina mění nekonstantní rychlostí jsou v následujících dvou cvičeních (první je s volbou s nabízených odpovědí).

Úkol Úkol Úkol

Volitelný obsah 4.2 (Změna funkce z rychlosti změny (prostorová změna teploty))

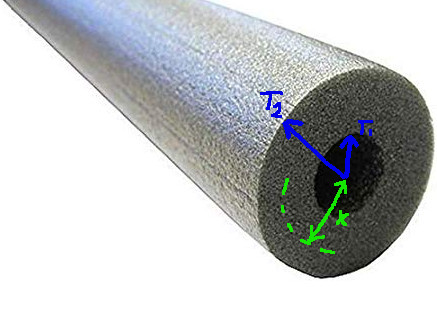
Obr. 4.4 Nákres pro nalezení vzorce pro tok tepla válcovou izolací.

Mějme ustálené proudění tepelnou izolací mezi dvěma soustřednými válcovými plochami. Délka izolace je \(\displaystyle L\), vnitřní a vnější poloměr jsou \(\displaystyle r\) a \(\displaystyle R\). Teploty uvnitř a vně jsou \(\displaystyle T_1\) a \(\displaystyle T_2\). Izolací prostupuje teplo rychlostí \(\displaystyle Q\), tj. každou myšlenou válcovou plochou o poloměru \(\displaystyle x\) projde za jednotku času teplo \(\displaystyle Q\). Cílem je najít vztah dávající uvedené veličiny do souvislosti. Odvodíme vztah, který jsme použili v přednášce o lokálních extrémech a slíbili dokázat později.

Z Fourierova zákona plyne, že teplo, které projde jednotkovou plochou za jednotku času, je úměrné záporně vzatému gradientu prostorové změně teploty, tj.

\[\frac{Q}{2\pi xL}=-k\frac {\mathrm dT}{\mathrm dx},\]

kde \(\displaystyle k\) je tepelná vodivost. Tento zákon definuje rychlost, s jakou se mění teplota v prostoru a my jej použijeme ke stanovení vztahu mezi tokem tepla a teplotním rozdílem mezi vnější a vnitřní stranou izolace. Snadnou úpravou dostáváme

\[\frac {\mathrm dT}{\mathrm dx} =-\frac{Q}{2k\pi xL}\]

a odsud

\[\Delta T= \int_r^R -\frac{Q}{2k\pi xL}\,\mathrm dx=-\frac{Q}{2k\pi L}\int_r^R \frac 1x\,\mathrm dx.\]

Protože platí

\[\int _r^R \frac 1x \,\mathrm dx= [\ln x]_r^R = \ln R-\ln r = \ln \frac Rr,\]

dostáváme po dosazení a vynásobení minus jedničkou vztah

\[-\Delta T=T_1-T_2=\frac{Q}{2k\pi L}\ln \frac Rr,\]

který jsme použili v přednášce o lokálních extrémech a slíbili dokázat později.

Stejný princip funguje pro libovolné ustálené proudění radiálním směrem při konstantní materiálové charakteristice. Stejný přístup je možné použít pro proudění podzemní vody popsané Darcyho zákonem (namísto Fourierova zákona) pro zvodeň namísto izolace (zvodeň je prostor kde se nachází a teče podzemní voda, tj. něco jako podzemní rybník nebo řeka zasypaná pískem nasáklým vodou) a piezometrickou výšku \(\displaystyle h\) namísto teploty (piezometrická výška udává, jak vysoko vystoupá voda ve zkušebním vrtu). Pokud máme zvodeň s napjatou hladinou (voda je pod tlakem sevřena mezi dvěma nepropustnými vrstvami), je vodivost konstantní. Rovnice popisující tuto situaci má tvar

\[h-h_0=\frac{Q}{2\pi T}\ln \frac r{r_0}\]

a nazývá se Thiemova rovnice.

Pokud sledujeme prostup tepla izolací, jejíž teplotní vodivost se mění s teplotou, není veličina \(\displaystyle k\) konstantní a proto výše uvedený postup není možné realizovat a odvozený vzorec pro takový případ neplatí. Stejná situace nastává u podzemní vody a proudění s volnou hladinou (není horní nepropustná vrstva zvodně). Takové úlohy vedou na jinou problematiku, kterou se naučíme řešit v kapitole s diferenciálními rovnicemi.

Poznámka (Změna veličiny vypočtená pomocí (jednodimenzionálního) gradientu)

Pokud se veličina \(\displaystyle f\) mění podél přímky v závislosti na veličině \(\displaystyle x\) na intervalu od \(\displaystyle x=a\) do \(\displaystyle x=b\) rychlostí \(\displaystyle r(x)\) (tj. \(\displaystyle r(x)=\frac{\mathrm df(x)}{\mathrm dx}\)), je změna veličiny \(\displaystyle f\) na intervalu \(\displaystyle [a,b]\) rovna

\[\Delta f=f(b)-f(a)=\int_a^b r(x)\,\mathrm dx.\]

4.2.2. Další motivace

Ze středoškolské fyziky dobře známe vzorce pro dráhu, práci a tlakovou sílu. Ovšem jenom v extrémně pěkných případech.

• Dráha rovnoměrného pohybu je určena vzorcem

  (4.1)\[s=vt.\]

  Tento vzorec není použitelný pro pohyb proměnnou rychlostí. Z kapitoly o neurčitém integrálu víme, že obecný vzorec je

  (4.2)\[s=\int v\,\mathrm dt.\]

  Pokud je \(\displaystyle v\) konstantní, vzorec (4.1) je důsledkem vzorce (4.2).

• Hydrostatická tlaková síla \(\displaystyle F\) působící ve vodě v hloubce \(\displaystyle h\) na plochu o velikosti \(\displaystyle S\) se určí podle vztahu

  \[F=Sh\rho g,\]
  kde \(\displaystyle \rho\) je hustota vody a \(\displaystyle g\) tíhové zrychlení. Tento vzorec však není možné použít, pokud různé části plochy jsou v různých hloubkách. Například není možné pomocí tohoto vzorce určit celkovou sílu na svislou stěnu reprezentující hráz přehrady.

• Práce vykonaná konstantní silou \(\displaystyle F\) po dráze \(\displaystyle s\) je

  (4.3)\[W=Fs.\]

  Co když se ale síla nebo dráha mění? Pokud nás zajímá práce nutná k navinutí visícího řetězu na rumpál, síla se během namotávání plynule zmenšuje, protože visící kus řetězu se při namotávání zkracuje. Pokud nás zajímá práce nutná k vyčerpání vodní nádrže, musíme každý litr vody, který je na dně, „tahat“ po delší dráze než každý litr vody, který je na hladině a proto se mění dráha. Vzorec (4.3) selhává v obou případech. Jednou kvůli nekonstantní síle, podruhé kvůli dráze.

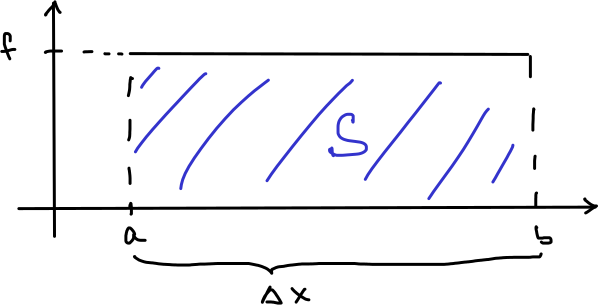
Obr. 4.5 Obsah pod konstantní funkcí.

• Obsah obrazce mezi konstantní funkcí \(\displaystyle f\) a osou \(\displaystyle x\) nad intervalem \(\displaystyle [a,b]\) se vypočte snadno, protože se jedná o obdélník se stranami \(\displaystyle f\) a \(\displaystyle \Delta x=b-a\). Proto

  \[S=f\cdot \Delta x.\]
  Tento přístup však není možné použít, pokud se funkce \(\displaystyle f\) na intervalu \(\displaystyle [a,b]\) mění. Formálně je tato úloha stejná jako ostatní úlohy výše, má však snadnou geometrickou interpretaci. Právě tuto interpretaci využijeme v následujícím k definici druhého typu určitého integrálu (Riemannova).

4.3. Určitý integrál (Riemannův)

Minivideo

Určitý integrál dokáže nahradit součin v případě, že koeficeint násobící měnící se veličinu není konstantní. Otevřít prezentaci

Obr. 4.6 Obsah pod konstantní funkcí.

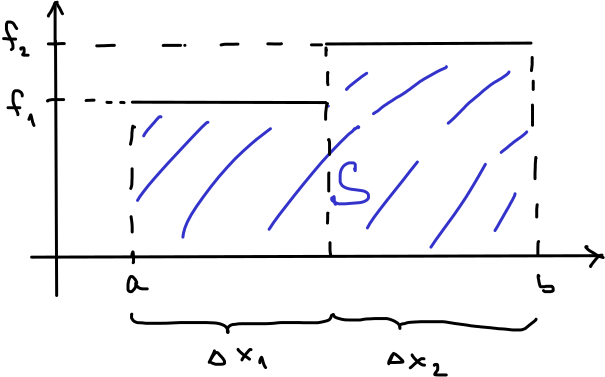
Obr. 4.7 Obsah pod funkcí po částech konstantní.

Obr. 4.8 Obsah pod obecnou funkcí je \(\displaystyle \int_a^b f(x)\,\mathrm dx\).

Úloha 1. Snadným důsledkem vzorce pro obsah obdélníka je obsah obrazce mezi grafem konstantní funkce a osou \(\displaystyle x\).

\[S=f\Delta x\]

Úloha 2. Obsah pod funkcí složené ze dvou konstantních funkcí napojených na sebe se vypočte jako součet obsahů dvou obdélníků.

\[S=f_1\Delta x_1+f_2\Delta x_2\]

Toto se dá snadno zobecnit na libovolný počet intervalů a pro libovolnou po částech konstantní funkci.

Prostředky matematické analýzy je možné „zjemňovat dělení do nekonečna“, přesněji, můžeme použít limitní přechod podobný limitnímu přechodu, který v definici derivace převedl podíl (průměrnou rychlost) na derivaci (okamžitou rychlost). Díky tomu není nutné se omezovat na po částech konstantní funkce, ale postup bude fungovat i pro velmi obecné funkce. Výsledným produktem je Riemannův integrál.

Riemannův integrál je velmi názorný, ale poměrně obtížně se počítá, pokud postupujeme přímo podle definice. Pokud však je funkce v určitém smyslu pěkná (má primitivní funkci na intervalu, který uvnitř obsahuje interval \(\displaystyle [a,b]\)) jsou Riemannův a Newtonův integrál stejné. Proto mezi nimi nerozlišujeme, používáme jeden pojem určitý integrál a počítáme jej pomocí definice Newtonova integrálu. Obsah obrazce pod křivkou \(\displaystyle f(x)\) je roven

\[S=\int_a^b f(x)\,\mathrm dx.\]

V teorii Riemannova integrálu má vzorec

\[\int_a^b f(x)\mathrm dx=\left[F(x)\right]_a^b=F(b)-F(a)\]

postavení věty nazývané Newtonova–Leibnizova věta a je to věta udávající, jak vypočteme určitý integrál pomocí neurčitého. Zajímavé je, že v některých případech je vhodné postupovat naopak a určit neurčitý integrál pomocí integrálu určitého, což si ukážeme v následující přednášce.

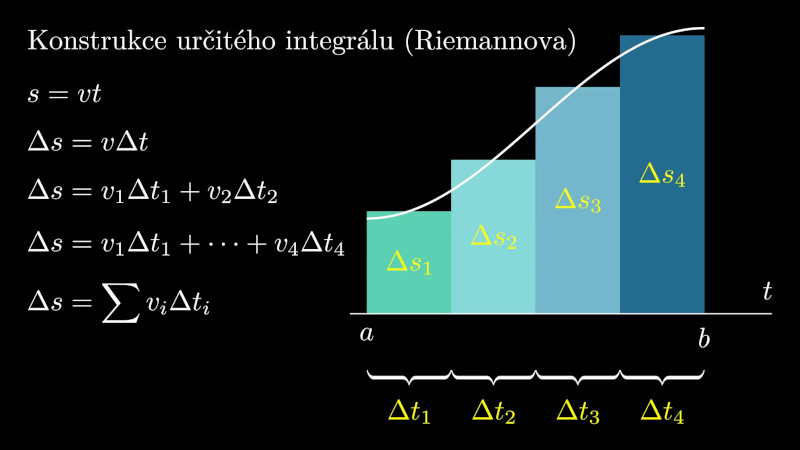
Volitelný obsah 4.3 (Nasčítání příspěvků k celkové dráze)

Obr. 4.9 Při pohybu proměnnou rychlostí je dráha integrálem rychlosti. Zdroj: pixabay.com

1. Těleso pohybující se po dobu \(\displaystyle \Delta t\) konstantní rychlostí \(\displaystyle v\) po přímce urazí dráhu

   \[s=v\Delta t.\]

2. Těleso pohybující se po dobu \(\displaystyle \Delta t_1\) konstantní rychlostí \(\displaystyle v_1\) po přímce a poté po dobu \(\displaystyle \Delta t_2\) rychlostí \(\displaystyle v_2\) urazí celkovou dráhu

   \[s=v_1\Delta t_1+v_2\Delta t_2.\]
   Toto je možné zobecnit na libovolný pohyb skládající se z konečného počtu úseků, kdy se těleso pohybuje konstantní rychlostí.
   \[s=v_1\Delta t_1+v_2\Delta t_2+\cdots +v_k \Delta t_k=\sum_{i=1}^k v_i\Delta t_i\]
   Příspěvek za každou část pohybu, kdy je rychlost konstantní, je
   \[\Delta s=v\Delta t, \]
   kde \(\displaystyle v\) a \(\displaystyle \Delta t\) jsou příslušná rychlost a doba pohybu, po kterou je rychlost konstantní.

3. Pokud se rychlost mění spojitě a \(\displaystyle a\) a \(\displaystyle b\) jsou počáteční a koncový okamžik pohybu, platí

   \[s=\int_a^b v(t)\,\mathrm dt.\]

Volitelný obsah 4.4 (Nasčítání příspěvků k celkové síle na přehradu)

Obr. 4.10 Celkovou sílu působící na jednu stěnu Mojžíšova mostu podle obrázku není možné určit středoškolským vzorcem, protože tlak není podél celé stěny konstantní, ale mění se s hloubkou. Zdroj: https://www.flickr.com/photos/huphtur

Obr. 4.11 Celkovou sílu působící na jednu stěnu mostu získáme jako součet sil na myšlené vodorovné pásy dělící tuto stěnu.

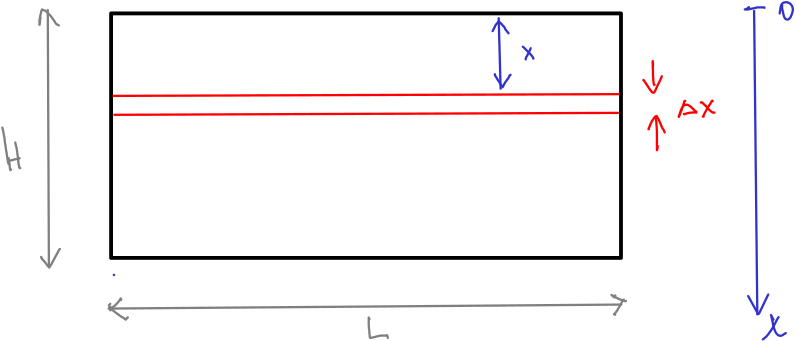
Mojžíšův most (Holandsko, pevnost Fort de Roovere) je v celosvětovém měřítku unikátním mostem. Je postavený ze dřeva a zanořený do vodního příkopu okolo pevnosti tak, aby splýval s krajinou. Představme si zjednodušeně, že vodní masu drží svislá dřevěná stěna a budeme se snažit najít celkovou sílu působící na tuto stěnu tlakem vodní masy. (Ve skutečnosti most leží na dně a dno se zvedá směrem ke stěnám mostu. Google umí najít stavební plán mostu.) Délku mostu označíme \(\displaystyle L\), výšku stěny (přesněji vzdálenost ode dna po hladinu vody) označíme \(\displaystyle H\).

1. Tlaková síla na rovinnou plochu o obsahu \(\displaystyle S\) vyvolaná tlakem \(\displaystyle p\) je rovna

   \[F=pS.\]
   Tlak v hloubce \(\displaystyle h\) je dán vzorcem
   \[p=h\rho g,\]
   kde \(\displaystyle \rho\) je hustota vody a \(\displaystyle g\) tíhové zrychlení.

2. Myšlenkově rozdělíme celou stěnu na části. Tlaková síla na celou stěnu je rovna součtu tlakových sil, které působí na jednotlivé části. Má smysl volit části tak, aby na nich byl tlak konstantní. Myšlenkově tedy stěnu rozřežeme na vodorovné pásky.

3. Na myšlený vodorovný pás, který má výšku \(\displaystyle \Delta x\) a je v hloubce \(\displaystyle x\), působí tlak \(\displaystyle p=x\rho g\). Obsah pásu je podle vzorce pro obsah obdélníka \(\displaystyle \Delta S=L\Delta x\). Celková síla působící na tento pás je

   \[\Delta F=p\Delta S=L\rho g x\Delta x.\]

4. Celkovou sílu na celou stěnu najdeme sečtením všech příspěvků. Formálně

   \[F=\sum L\rho g x\Delta x.\]
   Protože těchto příspěvků je nekonečně mnoho, sečteme je integrálem
   \[F=\int_0^H L\rho gx\,\mathrm dx.\]

5. Po výpočtu dostáváme

   \[F=\int_0^H L\rho gx\,\mathrm dx=L\rho g\int_0^H x\,\mathrm dx =L\rho g \left[\frac 12 x^2\right]_0^H=L\rho g \left[\frac 12 H^2-\frac 12 0^2\right]=\frac 12 LH^2 \rho g. \]
   Tento vztah je stejný, jako kdyby na celou plochu o velikosti \(\displaystyle LH\) působila tlaková síla vyvolaná tlakem \(\displaystyle \frac 12 H\rho g\), tj. tlakem v poloviční hloubce.

Volitelný obsah 4.5 (Nasčítání příspěvků k celkovému toku potrubím)

Obr. 4.12 Parabolické rozložení rychlosti v toku je nejen v potrubí, ale můžeme někdy pozorovat přímo v přírodě. Zdroj: pixabay.com (Anders Sandberg).

V předchozím příkladě jsme „krájeli“ přehradu na vodorovné pásy, protože ve vodorovném směru byl konstantní parametr, který jsme potřebovali mít konstantní pro výpočet k celkovému příspěvku. V následujícím případě je obdobný parametr konstantní na kružnicích a proto budeme dělit a sčítat příspěvky pomocí mezikruží.

V potrubí o poloměru \(\displaystyle R\) teče viskozní tekutina tak, že uprostřed má maximální rychlost a u stěn nulovou. Rychlost ve vzdálenosti \(\displaystyle r\) od osy potrubí je dána vztahem

\[v(r)=v_{max}\frac{R^2-r^2}{R^2}.\]

Střední rychlost dostaneme jako celkový tok potrubím dělený obsahem \(\displaystyle S=\pi R^2\). Tok v případě konstantní rychlosti je součinem rychlosti a obsahu průřezu. V případě rychlosti nekonstantní rozdělíme průřez na části \(\displaystyle \Delta S\), na každé části určíme příspěvek k celkovému toku a poté vše sečteme, tj.

\[Q=\sum_{\text{průřez}} v(r)\Delta S\]

Protože rychlost závisí na \(\displaystyle r\), je stejná na kružnicích a proto se jeví vhodné rozdělit průřez na mezikruží a sečíst přes poloměr těchto mezikruží. Budeme tedy integrovat přes proměnnou \(\displaystyle r\). Vyjádření \(\displaystyle Q\) přepíšeme do tvaru

\[Q=\sum_{\text{průřez}} v(r)\frac{\Delta S}{\Delta r}\Delta r\]

a limitním přechodem se změní suma na integrál a podíl změn na derivaci, tj.

\[Q=\int_0^R v(r)\frac{\mathrm d S}{\mathrm d r}\,\mathrm d r =\int_0^R v_{max}\frac{R^2-r^2}{R^2}\frac{\mathrm d S}{\mathrm d r}\,\mathrm d r .\]

Odsud pomocí \(\displaystyle S=\pi r^2\), \(\displaystyle \frac{\mathrm dS}{\mathrm dr}=2\pi r\) dostáváme po vytknutí konstant, roznásobení závorek a integraci

\[Q=\frac{2\pi v_{max}}{R^2}\int_0^R (R^2-r^2)r\,\mathrm dr=\frac{2\pi v_{max}}{R^2}\left[R^2\frac{r^2}{2}-\frac {r^4}4\right]_0^R =\frac{2\pi v_{max}}{R^2} \frac{R^4}{4} =\frac{v_{max}}{2} \pi R^2.\]

Tok je tedy formálně stejný, jako by voda tekla v celém průřezu rychlostí poloviční ve srovnání s maximální rychlostí ve středu trubice. Proto je \(\displaystyle \frac {v_{max}}2\) nazývána střední profilová rychlost průřezu.

(Volně podle Dana Říhová a Jana Marková, Poznámky k přednáškám z Hydrauliky, přednáška č. 3.)

Volitelný obsah 4.6 (Nasčítání příspěvků k celkovému momentu setrvačnosti tyče)

Obr. 4.13 Při posuzování stability rozhledny hraje moment setrvačnosti ústřední roli. Moment setrvačnosti rozhledny je možné získat součtem momentů setrvačnosti jednotlivých trámů. Rozhledna Bohdanka. Zdroj: http://tvstav.cz

Obr. 4.14 Tyč rotující okolo kolmé osy.

Obr. 4.15 Provazochodec při přechodu přes Grand Canyon. Zdroj: cbsnews.com

• Kinetická energie tělesa o hmotnosti \(\displaystyle m\) pohybujícího se posuvným pohybem rychlostí \(\displaystyle v\) je dána vztahem \(\displaystyle E=\frac 12 mv^2\). Kinetická energie tělesa o momentu setrvačnosti \(\displaystyle J\) pohybujícího se otáčivým pohybem úhlovou rychlostí \(\displaystyle \omega\) je dána vztahem \(\displaystyle E=\frac 12 J\omega ^2\). Odsud vidíme, že energie potřebná k vyvolání rotačního pohybu je úměrná momentu setrvačnosti. Moment setrvačnosti je tedy jakousi mírou odolnosti tělesa vůči silám, které se jej snaží uvést do rotačního pohybu. Zjednodušeně, větší moment setrvačnosti znamená, že těleso je stabilnější.

• Moment setrvačnosti hmotného bodu o hmotnosti \(\displaystyle m\) vzhledem k ose otáčení vzdálené \(\displaystyle r\) od tohoto bodu je \(\displaystyle J=mr^2\). Pro soustavu hmotných bodů stačí příspěvky sečíst. Pro případ tělesa se spojitě rozloženou hmotností bychom museli „sečíst nekonečně mnoho nekonečně malých příspěvků“ a proto sčítáme integrálem.

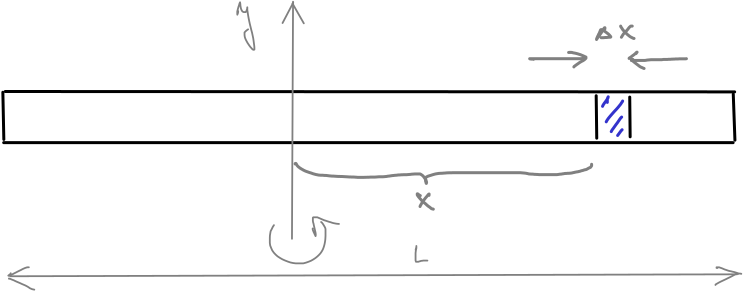
Budeme studovat rotaci tyče o hmotnosti \(\displaystyle m\) a délce \(\displaystyle L\) okolo osy kolmé k tyči. Nechť je tyč položena podél osy \(\displaystyle x\) a rotuje okolo osy \(\displaystyle y\). Kousek tyče o délce \(\displaystyle \Delta x\) má hmotnost \(\displaystyle \frac{\Delta x}{L}m\) a pokud je jeho vzdálenost od osy \(\displaystyle y\) rovna \(\displaystyle x\), příspěvek k celkovému momentu setrvačnosti je

\[\Delta J= \frac{\Delta x}{L}m x^2 =\frac{m}{L} x^2\Delta x.\]

Celkový moment setrvačnosti je dán integrálem, ale závisí na poloze tyče vzhledem k ose otáčení.

1. Pro tyč umístěnou levým koncem v počátku dostáváme moment vzhledem k ose procházející koncem tyče ve tvaru

   \[J=\int_0^L \frac{m}{L} x^2\,\mathrm dx=\frac mL \left[\frac 13 x^3\right]_0^L= \frac mL \frac 13 L^3=\frac 13 mL^2. \]

2. Pro tyč umístěnou středem v počátku dostáváme moment vzhledem k ose procházející středem ve tvaru

   \[J=\int_{-\frac L2}^{\frac L2} \frac{m}{L} x^2\,\mathrm dx=\frac mL \left[\frac 13 x^3\right]_{-\frac L2} ^{\frac L2} = \frac mL \left[\frac 13 \frac {L^3}8 - \frac 13 (-1)^3 \frac {L^3}8\right] = \frac 1{12} mL^2. \]

Závěr.

• Na roztočení tyče okolo konce je potřeba více energie, než na roztočení okolo středu. Čtyřikrát více. (Z praxe víme, že s dlouhým žebřem se manipuluje nejlépe, pokud jej držíme uprostřed.)

• Tyč o konstantní délkové hustotě \(\displaystyle \tau\) (dané použitým průřezem a materiálem) má hmotnost \(\displaystyle m=\tau L\) a moment setrvačnosti vzhledem ke středu

  \[J=\frac1{12}\tau L^3.\]
  Vidíme, že moment setrvačnosti roste dramaticky při zvětšování délky, s třetí mocninou. Proto provazochodci nosí na laně dlouhou tyč a proto při extrémních výkonech, jako je přechod Grand Canyon, bývá použita extrémně dlouhá tyč (pro Grand Canyon 9.1 metrů a 20 kilogramů, viz Nik Wallenda).

4.4. Shrnutí, hlavní myšlenky

Obr. 4.16 A jaká je hlavní message? Zdroj: pixabay.com

• Někdy máme zadánu rychlost, s jakou se mění veličina a potřebujeme znát funkční předpis pro tuto veličinu, tj. hodnotu v libovolném čase. To je úloha inverzní k derivaci a řeší ji neurčitý integrál.

• Při zadané rychlosti změny není možné bez zadání výchozího stavu určit hodnotu veličiny, která se mění. Je možné vypočítat jenom změnu této veličiny za určitý časový úsek (Newtonův určitý integrál) anebo je řešení dáno až na počáteční stav vyjádřený integrační konstantou v neurčitém integrálu.

• Někdy potřebujeme veličinu, která nás zajímá, najít posčítáním nekonečně mnoha příspěvků. Toto je v situaci, kdy se „za běhu“ mění parametry úlohy, například se během pohybu mění rychlost pohybu. V tomto případě používáme Riemannův určitý integrál, který je definovaný jinak než Newtonův, ale v prakticky zajímavých úlohách se počítá stejně.

• Další aplikací procesu opačného k derivování je úloha, kdy jsou vlastnosti křivky popsány pomocí derivace a hledáme rovnici pro tuto křivku. Příkladem jsou úlohy ve stavitelství a studiu materiálu (ohybová čára nosníku).