11. Dvojný integrál#

11.1. Motivace#

V praxi pracujeme s řadou veličin, které se počítají tak, že se parametr systému násobí obsahem.

Z plošné hustoty a obsahu násobením obdržíme hmotnost.
Z hloubky nádrže a obsahu obdržíme násobením objem.
Z tlaku a obsahu obdržíme násobením tlakovou sílu.

Je však otázka, jak tento přístup použít v případě, že daný parametr není po celé ploše na které je rozložen konstantní. Deska může být nehomogenní, nádrž nemusí mít vodorovné dno a ponořená deska nemusí mít všechny své části ve stejné hloubce.

Řešení této nesnáze je použití dvojného integrálu, který si nyní představíme.

11.1.1. Hmotnost nehomogenní desky#

../_images/table.jpg — Obr. 11.1 Deska s nekonstantní plošnou hustotou, https://www.flickr.com/photos/svacher, licence CC BY-NC-ND 2.0#

Hmotnost desky $\displaystyle \Omega$ je možno vypočítat jako součin plošné hustoty (hmotnost na jednotku obsahu) a obsahu desky.
\[M=\sigma S\]
Toto funguje pro desky s konstantní plošnou hustotou, kdy má deska ve všech místech stejné fyzikální vlastnostmi.
Pokud je deska slepená z konečného počtu malých homogenních desek o různých plošných hustotách, určíme hmotnost každé jednotlivé desky samostatně a výsledky potom sečteme.
\[m=\sigma_1 S_1+\sigma_2 S_2+\cdots + \sigma_n S_n\]
Pokud není možné nebo vhodné použít předchozí bod, musíme předpokládat, že hustota je obecnou funkcí. Potom namísto součtu konečného počtu sčítanců následuje nekonečný počet sčítanců a vybudujeme aparát, který nám umožní psát
\[m=\iint_\Omega \sigma \,\mathrm dS.\]

11.1.2. Objem vody v jezeře#

../_images/lake.jpg — Obr. 11.2 Nádrž s proměnnou hloubkou, https://www.pixabay.com#

Objem vody $\displaystyle V$ v nádrži nebo bazénu (se svislými stěnami, ale jinak i nepravidelného půdorysu $\displaystyle \Omega$) vypočteme jako součin obsahu hladiny $\displaystyle S$ a hloubky vody $\displaystyle h$, tj.
\[V=Sh\]
To ovšem platí jenom, pokud je v každém místě stejná hloubka.
Pokud má jedna část bazénu jinou hloubku než část druhá, vypočteme objem u každé hloubky samostatně a příspěvky sečteme, tj.
\[V=S_1h_1+S_2h_2.\]
Předchozí postup je možné aplikovat pro konečně mnoho hloubek, ale někdy to je nevhodné nebo, v případě spojitě se měnící hloubky, dokonce nemožné. Potom místo součtu konečně mnoha příspěvků použijeme dvojný integrál a dostáváme
\[V=\iint_\Omega h\mathrm dS.\]

11.1.3. Průtok v řece nebo v potrubí#

../_images/pipe.jpg — Obr. 11.3 Průtok potrubím je ovlivněn tím, že u stěny teče tekutina pomaleji než ve středu, potrubí na Aljašce, https://www.pixabay.com#

Teče-li průřezem $\displaystyle \Omega$ tekutina kolmo na průřez rychlostí $\displaystyle v$, je celkový průtok $\displaystyle Q$ (objem, který proteče průřezem za jednotku času) dán součinem
\[Q=vS,\]
kde $\displaystyle S$ je plošný obsah průřezu.
Teče-li různými místy průřezu voda různou rychlostí, sečteme jednotlivé příspěvky.
\[Q=v_1S_1+v_2S_2+\dots +v_nS_n\]
Myšlenku z předchozího bodu není snadné udělat, pokud se rychlost mění spojitě. Například v potrubí je rychlost rozdělena parabolicky a ubývá se vzdáleností od středu. Situaci zachraňuje dvojný integrál
\[Q=\iint_\Omega v\,\mathrm dS.\]

11.2. Dvojný integrál#

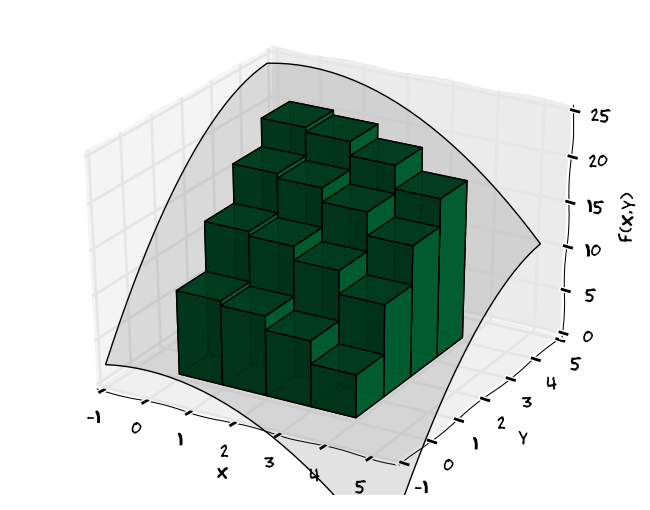
Uvažujme plošný materiál (desku) s danou plošnou hustotou. Budeme se snažit vypočítat hmotnost.

Pokud je deska homogenní, je její (plošná) hustota desky konstantní a její hmotnost je možno získat jednoduše jako součin této hustoty a obsahu.
Pokud deska není homogenní, ale skládá se z konečného počtu homogenních kousků, určíme postupem z minulého bodu hmotnost každého kousku a tyto hmotnosti poté sečteme.
Zbývá případ, kdy je hustota dána nějakou obecnou funkcí. Pokud se hustota desky mění a v obecném bodě $\displaystyle (x,y)$ je dána funkcí $\displaystyle f(x,y)$, můžeme myšlenkově rozdělit desku na malé kousky, v rámci každého malého kousku hustotu aproximovat konstantou a postupovat jako u desky z konečného počtu (malých) homogenních částí.
Získaná veličina je aproximací celkové hmotnosti. Pro jemnější dělení se přesnost aproximace zlepšuje.

V limitním přechodu kdy rozměry všech kousků na něž je deska dělena jde k nule dostáváme dvojný integrál

\[ \iint_\Omega f(x,y)\mathrm{d}x \mathrm{d}y , \]

kde $\displaystyle \Omega$ je oblast v rovině $\displaystyle (x,y)$ definovaná uvažovanou deskou. V aplikacích je častý též zápis

\[ \iint_\Omega f(x,y)\mathrm{d}A\]

nebo

\[ \iint_\Omega f(x,y)\mathrm{d}S.\]

11.3. Linearita a aditivita#

Dvojný integrál je odvozen (tak jako všechny integrály) pro aditivní veličiny a proto se „dobře snáší“ se sčítáním (ať už integrovaných funkcí, nebo integračních oborů) a s násobení integrované funkce konstantou. Přesněji, platí následující věty.

Věta (Linearita dvojného integrálu)

Buď $\displaystyle f_1$, $\displaystyle f_2$ funkce integrovatelné v $\displaystyle \Omega$ a $\displaystyle c_1$, $\displaystyle c_2$ libovolná reálná čísla. Platí

\[ \iint_{\Omega} \bigl[c_1f_1(x,y)+c_2f_2(x,y)\bigr]\mathrm dx\mathrm dy = c_1\iint_{\Omega} f_1(x,y)\mathrm dx\mathrm dy+ c_2\iint_{\Omega} f_2(x,y)\mathrm dx\mathrm dy \]

Věta (Aditivita vzhledem k oboru integrace)

Nechť je množina $\displaystyle \Omega$ rozdělena na dvě oblasti $\displaystyle \Omega_1$ a $\displaystyle \Omega_2$, které mají společné nejvýše hraniční body. Platí

\[ \iint_\Omega f(x,y)\mathrm dx\mathrm dy= \iint_{\Omega_1} f(x,y)\mathrm dx\mathrm dy+ \iint_{\Omega_2} f(x,y)\mathrm dx\mathrm dy. \]

11.4. Výpočet#

11.4.1. Výpočet pro oblast mezi funkcemi proměnné $\displaystyle x$#

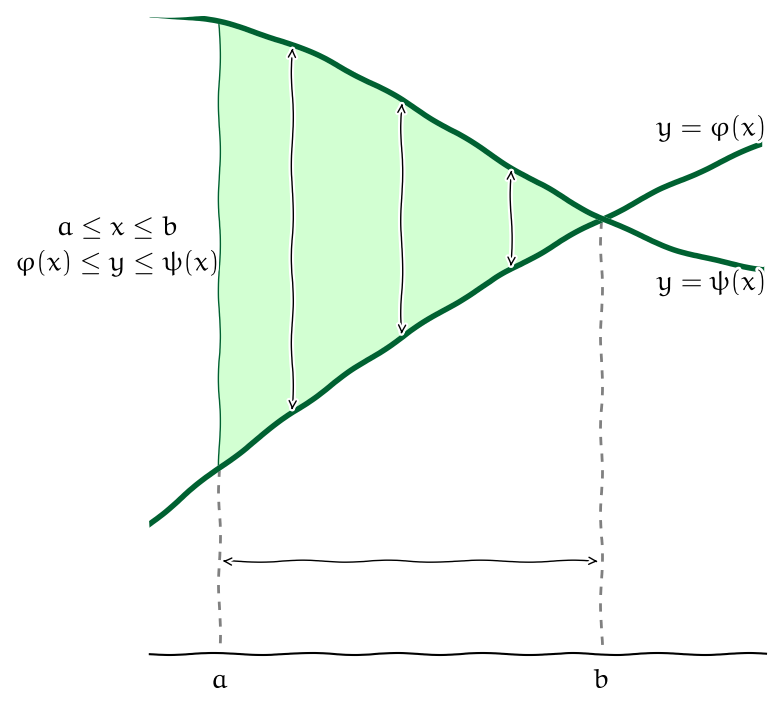
../_images/fub_1.png — Obr. 11.4 Oblast mezi funkcemi proměnné $\displaystyle x$.#

V závislosti na tom, jakými nerovnostmi množinu $\displaystyle \Omega$ definujeme, můžeme pro výpočet dvojného integrálu použít následující věty. Tyto věty udávají, jak je možno dvojný integrál přepsat jako dvojnásobný integrál. Mají název Fubiniovy věty.

Věta (Fubiniova věta)

Nechť $\displaystyle f$ je funkce spojitá v uzavřené oblasti

\[ \Omega=\{(x,y)\in\mathbb{R}^2:{a\leq x\leq b}\text{ a } {\varphi (x)\leq y\leq \psi (x)}\}.\]

Potom

\[ \iint_{\Omega}f(x,y)\mathrm{d}x \mathrm{d}y ={\int_{a}^{b}} \Bigl[ \int_{\varphi (x)}^{\psi(x)} f(x,y){\mathrm{d}y }\Bigr]{\mathrm{d}x }. \]

11.4.2. Výpočet pro oblast mezi funkcemi proměnné $\displaystyle y$#

```{figure} fub_2.png Oblast mezi funkcemi proměnné $y$. ```

Věta (Fubiniova věta pro jiné pořadí integrace)

Nechť $\displaystyle f$ je funkce spojitá v uzavřené oblasti

\[ \Omega=\{(x,y)\in\mathbb{R}^2:{a\leq y\leq b}\text{ a } {\varphi (y)\leq x\leq \psi (y)}\}. \]

Potom

\[ \iint_{\Omega}f(x,y)\mathrm{d}x \mathrm{d}y ={\int_a^b}\Bigl[ {\int_{\varphi (y)}^{\psi(y)}} f(x,y){\mathrm{d}x }\Bigr]{\mathrm{d}y }. \]

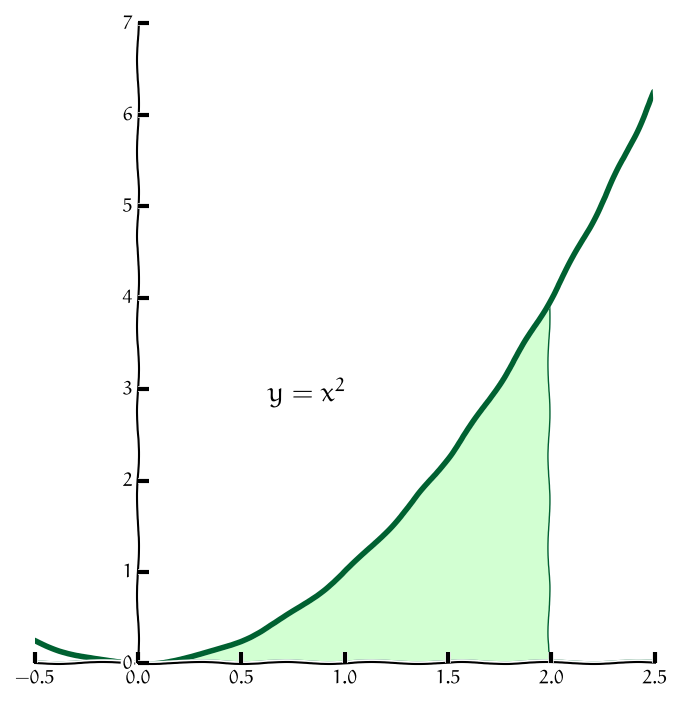
../_images/fub_4.png — Obr. 11.5 Oblast, pro kterou jsou možná obě pořadí integrace.#

11.4.3. Problematika záměny pořadí integrace#

Často je možné oblast integrace zapsat pomocí obou možností uvedených na předchozích slidech. Například oblast na obrázku je možno zapsat buď jako

\[\begin{split}\begin{gathered} 0\leq x \leq 2\\ 0\leq y\leq x^2 \end{gathered}\end{split}\]

nebo

\[\begin{split}\begin{gathered} 0\leq y \leq 4\\ \sqrt{y}\leq x\leq 2. \end{gathered}\end{split}\]

Pro integrál funkce $\displaystyle f(x,y)$ přes takovou množinu tedy máme dvě alternativy:

\[\int_0^2 \int _0^{x^2} f(x,y)\;\mathrm{d}y\;\mathrm{d}x\]

\[\int_0^4 \int _{\sqrt y}^{2} f(x,y)\;\mathrm{d}x\;\mathrm{d}y.\]

Všimněte si, že nestačí prosté prohození integrálů. Je nutno přepočítávat meze a hraniční křivky je nutno vyjádřit jednou jako funkce proměnné $\displaystyle x$ a jednou jako funkce proměnné $\displaystyle y$. V důsledku tohoto dochází v průběhu výpočtu dvěma různými způsoby k tomu, že pracujeme se dvěma různými integrály. Výsledky jsou stejné, nemusí však být dosažitelné srovnatelnou námahou, jedna z cest může být snazší.

11.4.4. Výpočet pro obdélníkovou oblast#

```{figure} fub_3.png Integrál přes obdélník. ```

Výše uvedené problémy se stanovením a případným přepočítáváním mezí při záměně pořadí integrace se nevyskytují při integrování přes obdélníkovou oblast.

Věta (Fubiniova věta na obdélníku)

Nechť $\displaystyle R=[a,b]\times[c,d]$ je uzavřený obdélník v $\displaystyle \mathbb{R}^2$ a $\displaystyle f$ funkce definovaná a spojitá na $\displaystyle R$. Pak platí

\[\begin{split} \begin{aligned}\iint_R f(x,y)\mathrm{d}x \mathrm{d}y &= \int_a^b\Bigl[\int_c^d f(x,y)\mathrm{d}y \Bigr]\mathrm{d}x \\&= \int_c^d\Bigl[\int_a^b f(x,y)\mathrm{d}x \Bigr]\mathrm{d}y .\end{aligned} \end{split}\]

Platí-li dokonce rovnost $\displaystyle f(x,y)=g(x)h(y)$, pak

\[ \iint_R f(x,y)\mathrm{d}x \mathrm{d}y = \int_a^b g(x) \mathrm{d}x \int_c^d h(y)\mathrm{d}y . \]

11.5. Aplikace dvojného integrálu#

11.5.1. Matematické aplikace dvojného integrálu#

Obsah $\displaystyle \mu(\Omega)$ množiny $\displaystyle \Omega$ vypočteme jako integrál
\[\mu(\Omega)=\iint_\Omega \mathrm{d}x \mathrm{d}y.\]
Integrální střední hodnota funkce $\displaystyle f(x,y)$ definované na množině $\displaystyle \Omega$ je
\[ \frac{\iint_\Omega f(x,y)\mathrm{d}x \mathrm{d}y }{\mu (\Omega)},\]
kde $\displaystyle \mu (\Omega)=\iint_\Omega\mathrm{d}x\mathrm{d}y$ je obsah množiny $\displaystyle \Omega$.

11.5.2. Objem kopce nebo jezera pomocí vrstevnic#

../_images/fuji.jpg — Obr. 11.6 Posvátná hora Japonska. Objem se dá určit pomocí obsahů vrstevnic.#

Obsah množiny ohraničené vrstevnicí na mapě vynásobený rozestupem mezi vrstevnicemi je přibližně roven objemu vrstvy mezi dvěma vrstevnicemi.
Pokud sečteme obsahy všech vrstevnic a vynásobíme rozestupem mezi těmito vrstevnicemi, dostaneme odhad pro objem kopce. Vlastně je to jako bychom kopec rozřezali na stejně tlusté plátky, naskládali je vedle sebe, sečetli obsahy postav takto vzniklých těles a vynásobili výškou.
Podobně je možné odhadnout objem jezera.
V tomto případě je dvojný integrál pouze koncept. Samozřejmě nemáme ambice vyjadřovat vrstevnice v analytickém tvaru a integrovat pomocí Fubiniovy věty. Ke slovu přijde spíše numerický výpočet integrálu.

11.5.3. Fyzikální aplikace dvojného integrálu#

Hmotnost množiny $\displaystyle M$ je
\[m=\iint_M \sigma(x,y)\mathrm{d}x \mathrm{d}y,\]
kde $\displaystyle \sigma(x,y)$ je plošná hustota (hmotnost vztažená na jednotku povrchu).
Lineární momenty hmotné množiny $\displaystyle M$ vzhledem k osám $\displaystyle y$ a $\displaystyle x$ jsou rovny
\[\iint_M x\sigma(x,y)\mathrm{d}x \mathrm{d}y\]
a
\[\iint_M y\sigma(x,y)\mathrm{d}x \mathrm{d}y.\]
Moment setrvačnosti hmotné množiny $\displaystyle M$ vzhledem k ose je
\[J=\iint_M \rho^2(x,y)\sigma(x,y)\mathrm{d}x \mathrm{d}y ,\]
kde $\displaystyle \rho(x,y)$ je vzdálenost bodu $\displaystyle (x,y)$ od osy otáčení. Například pro osu $\displaystyle x$ je $\displaystyle \rho(x,y)=y$ a pro osu $\displaystyle y$ je $\displaystyle \rho (x,y)=x$. Pro osu procházející kolmo počátkem je $\displaystyle \rho(x,y)=\sqrt{x^2+y^2}$.

11.5.4. Techniké aplikace dvojného integrálu#

../_images/I-nosniky.jpg — Obr. 11.7 Dřevostavba realizovaná pomocí I-nosníků. I-nosníky mají vysoký kvadratický moment při nízké spotřebě materiálu. Proto jsou tuhé a silné i při nízké hmotnosti. Ve strojařině se používají odedávna, první dřevostavba z nosníků tohoto typu byla v ČR realizována 2011. Zdroj: https://www.taus.eu#

Souřadnice těžiště množiny jsou podílem lineárních momentů a celkové hmotnosti množiny.
Kvadratický moment průřezu (což je moment setrvačnosti pro $\displaystyle \sigma(x,y)=1$, anglicky second moment of area) je veličina, která hraje podstatnou roli v mechanice (nábytek, stavby) při dimenzování (polic, nosných tyčí, nosníků).
V technické praxi zpravidla neuvažujeme nekonstantní plošnou hustotu. Potom je možné je bez újmy na obecnosti nahradit jedničkou. Vzorce pro obsah, $\displaystyle x$-ovou souřadnici těžiště ($\displaystyle x_0$), $\displaystyle y$-ovou souřadnici těžiště ($\displaystyle y_0$), kvadratický moment vzhledem k ose $\displaystyle x$ ($\displaystyle I_x$) a kvadratický moment vzhledem k ose $\displaystyle y$ ($\displaystyle I_y$) (pro množinu $\displaystyle M$ s plošnou hustotou $\displaystyle 1$) jsou
\[\begin{split} \begin{alignedat}{2} % S&=\iint_M\mathrm{d}x \mathrm{d}y \\ x_0&=\frac 1S \iint_M x\mathrm{d}x \mathrm{d}y ,&\qquad I_x&= \iint_M y^2\mathrm{d}x \mathrm{d}y, \\ y_0&=\frac 1S \iint_M y\mathrm{d}x \mathrm{d}y , & I_y&= \iint_M x^2\mathrm{d}x \mathrm{d}y, \\ \end{alignedat} \end{split}\]
kde $\displaystyle S=\mu (M)$ je obsah množiny $\displaystyle M$. Poloha těžiště je tedy střední hodnotou funkcí $\displaystyle x$ a $\displaystyle y$.

11.5.5. Praktické aplikace dvojného integrálu - tuhost nosníků, stabilita stromů#

../_images/beam1.jpg — Obr. 11.8 Tuhost a nosnost nosníků nebo podpěr souvisí s kvadratickým momentem průřezu. Zdroj: pixabay.com#

../_images/vanocni_strom.jpg — Obr. 11.9 Poloviční poloměr znamená u homogenního materiálu šestnáctkrát menší tuhost. Tedy jenom šest procent původní tuhosti! U stromu je tento poměr ještě horší díky různým druhům dřeva uprostřed a na kraji. Vánoční strom pro Prahu na Vánoce 2019. Zdroj: Taiko, Pražský deník#

Tuhost (odolnost vůči deformaci) pro nosník obdélníkového průřezu o výšce $\displaystyle b$ a šířce $\displaystyle a$ je dána kvadratickým momentem obdélníkového průřezu vzhledem k vodorovné ose procházející těžištěm.

\[\begin{split}\begin{aligned}I_x&= \iint_{\left[-\frac a2,\frac a2\right]\times \left[-\frac b2,\frac b2\right]} y^2\,\mathrm dx\mathrm dy\\ &= \int_{-\frac a2}^{\frac a2} \,\mathrm dx\int_{-\frac b2}^{\frac b2} y^2 \,\mathrm dy= a\left[\frac 13 y^3\right]_{-\frac b2}^{\frac b2} =\frac 1{12}ab^3 \end{aligned} \end{split}\]

Odsud máme okamžitě několik pozorování

Pokud šířka vzroste dvakrát, tuhost vzroste také dvakrát. Pokud ale dvakrát vzroste výška, tuhost vzroste dokonce osmkrát. Pro nosník s poměrem stran 1:2 je poměr tuhostí při poloze naplacato a nastojato roven 1:4.
Pro nosník čtvercového průřezu ($\displaystyle a=b$) roste tuhost se čtvrtou mocninou rozměrů. Obsah (a tedy i hmotnost) roste s druhou mocninou. Pokud tedy u nosníku se čtvercovým průřezem zdvojnásobíme množství materiálu, tuhost vzroste čtyřnásobně. Toto si můžeme představit tak, že jsme původní nosník obalili trubkou vyrobenou ze stejného množství materiálu. Protože společná tuhost je čtyřnásobná, znamená to, že přidaná trubka má trojnásobnou tuhost než původní tyč. Proto se v konstrukcích nepoužívají tyče, ale trubky nebo analogické struktury (I-čka apod). I příroda zná tyto zákonitosti a kosti tvořící opěrný aparát živočichů jsou trubkovitého tvaru.
Pro čtvercový průřez roste tuhost se čtvrtou mocninou délky strany
\[I_x=\frac 1{12} a^4.\]
Stejná závislost (přímá úměrnost mezi kvadratickým momentem a čtvrtou mocninou rozměru) musí být u každého průřezu jednoparametrického tvaru, například pro kruh. To plyne například z věty nazývané Buckinghamův $\displaystyle \Pi$ teorém. Jako aplikaci uvažujme strom modelovaný jako nosník s kruhovým průřezem. Například strom, ve kterém je dutina o velikosti poloviny průměru kmene většinou vyvolá obavy ze stability. I když taková dutina vypadá obrovská, tuhost se sníží o původní tuhost vynásobenou koeficientem
\[(0.5)^4=0.0625\approx 6\%.\]
Vidíme, že i s hrozivě vypadající dutinou má kmen pořád tuhost $\displaystyle 94\%$ původní tuhosti (za předpokladu dutiny uprostřed kmene). Z hlubšího fyzikálního rozboru, který je nyní nad rámec našeho popisu, pevnost roste jenom s třetí mocninou a proto odolnost vůči zlomení klesne o něco více než tuhost.

11.5.6. Aplikace dvojného integrálu - těžiště složeného obrazce#

Uvažujme množinu $\displaystyle M$ s jednotkovou plošnou hustotou, rozdělenou na dvě disjunktní části $\displaystyle M_1$ a $\displaystyle M_2$. Tyto množiny mají $\displaystyle x$-ovou polohu těžiště v bodě

\[x_{0i}=\frac1{S_i}{\iint_{M_i}x\,\mathrm dx\mathrm dy}, \qquad S_i=\iint_{M_i}\,\mathrm dx\mathrm dy,\qquad i=1,2.\]

Poloha těžiště není aditivní veličinou. Dvojný integrál však aditivní veličinou je. Platí

\[\begin{split} \begin{aligned} \iint _{M} x\,\mathrm dx\mathrm dy&=\iint _{M_1} x\,\mathrm dx\mathrm dy + \iint _{M_2} x\,\mathrm dx\mathrm dy\\ &=S_1 x_{01} + S_2 x_{02} \end{aligned} \end{split}\]

a těžiště množiny $\displaystyle M$ je

\[\begin{split} \begin{aligned} x_0&=\frac 1{S_1+S_2}\iint _{M} x\,\mathrm dx\mathrm dy\\ &=\frac 1{S_1+S_2}(S_1 x_{01} + S_2 x_{02})\\ &=\frac {S_1 x_{01} + S_2 x_{02}}{S_1+S_2}. \end{aligned} \end{split}\]

Totéž je možné provést pro $\displaystyle y$-ovou souřadnici, nebo pro libovolný konečný počet částí. Podobně je možné odvodit vzorec s obecnou nekonstantní plošnou hustotou. Poloha těžiště složeného obrazce je tedy váženým průměrem těžišť jednotlivých složek, kde váha každé složky je určena její hmotností. Protože se jedná o vážený průměr, tj. vlastně o lineární kombinaci bodů, kdy součet koeficientů je roven jedné, okamžitě vidíme, že těžiště složeného obrazce je na úsečce mezi těžišťmi jednotlivých částí.

Zobecnění výše uvedených myšlenek na množinu rozdělenou na více částí je již snadné.

11.5.7. Aplikace dvojného integrálu - Steinerova věta#

Nechť je dána množina $\displaystyle M$ s plošnou hustotou $\displaystyle \sigma(x,y)$. Ukážeme, že vzhledem k ose procházející těžištěm je nejmenší moment setrvačnosti. Ukážeme si dále, že pomocí momentu setrvačnosti vzhledem k ose procházející těžištěm je možné vyjádřit momenty setrvačnosti i k libovolným rovnoběžným osám. Pro jednotkovou plošnou hustotu dostáváme jako speciální případ vzorce pro kvadratický moment, důležité ve statice.

Nechť $\displaystyle m=\iint \sigma(x,y)\,\mathrm dx\mathrm dy$, $\displaystyle y_0=\frac 1{m}\iint_M y\sigma(x,y)\,\mathrm dx\mathrm dy$ a $\displaystyle I_{xT}=\iint_M (y-y_0)^2\sigma(x,y)\,\mathrm dx\mathrm dy$ jsou hmotnost, $\displaystyle y$-ová poloha těžiště a moment setrvačnosti vzhledem k ose jdoucí těžištěm rovnoběžně s osou $\displaystyle x$. Moment setrvačnosti vhledem k ose $\displaystyle x$ je

\[I_{x0}=\iint y^2\sigma(x,y)\,\mathrm dx\mathrm dy.\]

Platí (píšeme zkráceně $\displaystyle \sigma$ místo $\displaystyle \sigma(x,y)$)

\[\begin{split}\begin{aligned} I_{xT}&=\iint_M (y-y_0)^2\sigma\,\mathrm dx\mathrm dy\\ &=\iint_M (y^2-2yy_0+y_0^2)\sigma\,\mathrm dx\mathrm dy\\ &=\iint_M y^2\sigma\,\mathrm dx\mathrm dy -2y_0 \iint_M y\sigma\,\mathrm dx\mathrm dy +y_0^2 \iint_M \sigma\,\mathrm dx\mathrm dy\\ &=I_{x0} -2y_0 m y_0 + y_0^2 m \\ &=I_{x0} -m y_0^2. \end{aligned} \end{split}\]

Odsud dostáváme

\[I_{x0}=I_{xT}+my_0^2,\]

což lze interpretovat tak, že moment setrvačnosti vhledem k ose $\displaystyle o$ je součtem momentu setrvačnosti vzhledem k ose procházející těžištěm rovnoběžně s $\displaystyle o$ a momentu setrvačnosti hmotného bodu ležícího v těžišti množiny a o stejné hmotnosti jako je hmotnost množiny vzhledem k ose $\displaystyle o$.

11.5.8. Aplikace dvojného integrálu - tlak na svislou plochu#

../_images/bobri.jpeg — Obr. 11.10 Bobři v ZOO v Brně jsou za skleněnou stěnou obdélníkového tvaru.#

Vzorec pro tlakovou sílu $\displaystyle F=pS$ není možné použít například pro výpočet celkové síly působící na svislou stěnu nebo hráz, protože tlak $\displaystyle p$ se mění s hloubkou a není tedy konstantní na celém průřezu o obsahu $\displaystyle S$. Pro obdélníkovou stěnu jsme úlohu vyřešili (viz Mojžíšův most) pomocí integrálu, pro stěnu obecného tvaru použijeme integrál dvojný.

Uvažujme svislou rovinnou hráz $\displaystyle M$. Hrází je přitom myšlena rovinná množina s jednotkovou plošnou hustotou, ne postavený trojrozměrný objekt. Počátek kartézské soustavy souřadnic volíme u hladiny, osa $\displaystyle y$ směřuje dolů, osa $\displaystyle x$ vodorovně. Tlak v hloubce $\displaystyle y$ je roven $\displaystyle p=y\rho g$, kde $\displaystyle \rho$ je hustota vody a $\displaystyle g$ tíhové zrychlení. Na plochu o rozměrech $\displaystyle \Delta S$ v hloubce $\displaystyle y$ působí tlaková síla

\[\Delta F=y\rho g \Delta S.\]

Tato tlaková síla má ve všech bodech hráze stejný směr a celkovou sílu na hráz je možno zjistit sečtením sil v jednotlivých bodech. Podobná myšlenková úvaha jako v úvodu pro hmotnost desky, nebo přesný matematický popis, nás dovedou k tomu, že celková síla na hráz je dána integrálem

\[F=\iint _M y\rho g \,\mathrm d x\mathrm dy.\]

Protože $\displaystyle g$ a $\displaystyle \rho$ jsou konstanty, je možno psát

\[F=\rho g\iint _M y \,\mathrm d x\mathrm dy.\]

Využijeme-li vzorec pro $\displaystyle y$-ovou souřadnici těžiště, má výsledný vztah tvar

\[F=\rho g y_0 S,\]

kde $\displaystyle S$ je obsah hráze. Formálně tento vztah odpovídá vzorci

(11.1)#\[F=p_0 S,\]

kde $\displaystyle p_0=\rho g y_0$ je tlak v těžišti. Proto v praxi stačí znát těžiště hráze a pro výpočet síly na hráz použít celkovou plochu hráze a tlak v těžišti. Protože jsme pracovali s obecnou množinou $\displaystyle M$, není tento poznatek nijak vázán na konkrétní tvar hráze. Musí být však splněna podmínka, že všechny body hráze leží v jedné rovině.

Ve výpočtu výše jsme uvažovali svislou rovinu, ale zobecnění na šikmou rovinu je snadné. Stačí opravit vztah pro hloubku, protože když svislou množinu i s kartézskými souřadnicemi pootočíme okolo osy procházející hladinou, hloubka všech bodů se sníží faktorem $\displaystyle \sin \alpha$, kde $\displaystyle \alpha$ je úhel mezi vodorovnou hladinou a rovinou hráze. Formálně tato operace dopadne stejně, jako kdybychom tekutinu nahradili tekutinou s hustotou $\displaystyle \sin\alpha$-krát nižší. Protože však vztah (11.1) nezávisí na hustotě, nic se na něm nezmění. Také zobecnění na několik rovin je snadné. Zobecnění na zakřivenou plochu je náročnější a vyžaduje jiný typ integrálu.

V předchozím textu jsme proměnnou veličinu popisující tlak na hráz jako funkci hloubky nahradili konstantní veličinou, udávající tlak v těžišti. Výsledný účinek na hráz se nezměnil. To je přesně smysl střední hodnoty. V matematických pojmech je možno říci, že střední hodnota tlaku na svislou hráz je rovna tlaku v těžišti hráze. (Protože hrází myslíme spíše rovinnou plochu, tak by přesnější terminologie měla používat raději pojem geometrický střed. Budeme se však držet ustálené terminologie.)

Nikde ve výpočtu jsme nepoužili konkrétní meze pro integraci. Výsledek tedy platí nejenom pro hráz dosahující k hladině, ale například i pro poklop výpusti, který je celý pod vodou.

11.5.9. Aplikace dvojného integrálu - působiště tlakové síly#

Budeme pokračovat v předchozím příkladě a hledat působiště výsledné tlakové síly.

Tlaková síla působící na svislou hráz má celkový nulový moment vzhledem k ose proházející působištěm. Je-li hráz definována množinou $\displaystyle M$ a je-li $\displaystyle y_c$ působiště výsledné tlakové síly, je v hloubce $\displaystyle y$ tlak na plošku o velikosti $\displaystyle \Delta S$ roven $\displaystyle y\rho g \Delta S$ a součin $\displaystyle (y_c-y)y\rho g\Delta S$ je příspěvek k otáčivému momentu vzhledem k ose, procházející vodorovně působištěm tlakové síly. Součet všech těchto příspěvků se nuluje, tedy musí platit

\[\iint_M (y_c-y)y\rho g\,\mathrm dx\mathrm dy=0.\]

Odsud po vydělení konstantami $\displaystyle \rho g$ dostáváme

\[\iint_M (y_c-y)y\,\mathrm dx\mathrm dy=0\]

a po roznásobení závorky, rozdělení integrálu na dva a vytknutí konstanty

\[y_c\iint_M y\,\mathrm dx\mathrm dy = \iint_M y^2\,\mathrm dx\mathrm dy.\]

Nyní již snadno dostaneme výsledný vztah

(11.2)#\[y_c=\frac{\iint_M y^2\,\mathrm dx\mathrm dy}{\iint_M y\,\mathrm dx\mathrm dy}.\]

Pokud je množina $\displaystyle M$ obdélník, je možné ji (po vhodné změně jednotek) brát jako jednotkový čtverec. Protože platí

\[\iint_{[0,1]\times [0,1]}y\,\mathrm dx\mathrm dy=\frac 12, \quad \iint_{[0,1]\times [0,1]}y^2\,\mathrm dx\mathrm dy=\frac 13, \]

dostáváme $\displaystyle y_c=\frac{\frac 13}{\frac 12}=\frac 23$ a působiště na obdélníkovou hráz je v hloubce odpovídající dvěma třetinám celkové hloubky.

Formálně vztah pro $\displaystyle y_c$ odpovídá vztahu pro těžiště množiny s plošnou hustotou $\displaystyle y$. Na tomto pozorování a na skutečnosti, že u pravidelných množin umíme těžiště najít geometricky, je založena metoda nalezení působiště tlakové síly pomocí zatěžovacího obrazce.

Kvadratický moment v čitateli zlomku (11.2) vyjadřujícího $\displaystyle y_c$ je často výhodnější rozepsat pomocí Steinerovy věty. Ve jmenovateli je součin obsahu $\displaystyle S$ a $\displaystyle y$-ové souřadnice těžiště $\displaystyle y_0$. Tím dostaneme

\[y_c=\frac{I_{x0}+Sy_0^2}{Sy_0}=\frac{I_{x0}}{Sy_0}+y_0,\]

kde $\displaystyle I_{x0}$ je kvadratický moment vzhledem k ose procházející vodorovně těžištěm. Působiště tlakové síly $\displaystyle y_c$ je tedy posunuto směrem dolů od těžiště $\displaystyle y_0$ o hodnotu odpovídající kvadratickému momentu vzhledem k vodorovné ose těžištěm $\displaystyle I_{x0}$ vyděleném součinem obsahu hráze $\displaystyle S$ a $\displaystyle y$-ové polohy těžiště $\displaystyle y_0$.

11.6. Shrnutí, hlavní myšlenky#

../_images/message.jpg — Obr. 11.11 A jaká je hlavní message? Zdroj: pixabay.com#

Mnoho veličin, které nás zajímají, počítáme jako součin obsahu plochy s nějakou jinou veličinou. Zpravidla veličina kterou takto počítáme souvisí v objektem jako s celkem a veličina, kterou násobíme s plochou, souvisí se situací v jednom konkrétním místě. Například hmotnost desky z plošného materiálu (vlastnost objektu) je součinem plošné hustoty (charakteristika materiálu) a obsahu. Celková tlaková síla na hráz (vlastnost objektu) je součinem tlaku (vlastnost v daném bodě) a obsahu. Problém však nastane, pokud vlastnosti nejsou všude stejné. Například plošný materiál může mít v různých místech různé vlastnosti, nebo tlak může být v každém místě hráze jiný, protože hráz je napříč více hloubkami. V takových případech je potřeba součin něčím nahradit. Příslušná náhrada je dvojný integrál.
Vidíte dvojný integrál a potřebujete promyslet, co vyjadřuje? Představte si, že integrovaná veličina je konstantní. Potom se integrál redukuje na součin a ten už zpravidla je snadné vyjádřit slovně. Například dvojný integrál hloubky jezera vypočítaný přes celé jezero. Pro konstantní hloubku se tato veličina redukuje na součin hloubky a obsahu hladiny. To je ale objem jezera. Proto dvojný integrál hloubky jezera vyjadřuje objem vody v jezeře.
Dvojný integrál počítáme převodem na dvojnásobný integrál, tj. dva integrály, z nichž jeden je uvnitř druhého. V některých situacích (integrál funkce sestavené jako součin funkcí jedné proměnné a počítaný přes obdélník) se dokonce může situace redukovat na součin dvou integrálů funkce jedné proměnné.
Dvojný integrál je také odpověď na problém, jak sesčítat veličinu rozloženou v ploše (kvadratický moment obrazce, veličina důležitá pro posuzování tuhosti a pevnosti nosníků) nebo jak ji zprůměrovat (integrální střední hodnota funkce dvou proměnných).

Dvojný integrál

Obsah