10. Autonomní rovnice a systémy#
Úmluva
V celé přednášce budeme jako nezávislou proměnnou uvažovat čas \(\displaystyle t\). Autonomní znamená v tomto kontextu nezávislý na čase. Budeme studovat rovnice mající tuto vlastnost. Budeme dále studovat systémy, které mají dostatečně pěkná data na to, aby byla zaručena jednoznačnost řešení. To je například, pokud funkce na pravé straně rovnice má ohraničené parciální derivace, což bude v níže uvedených příkladech vždy splněno.
10.1. Autonomní diferenciální rovnice#
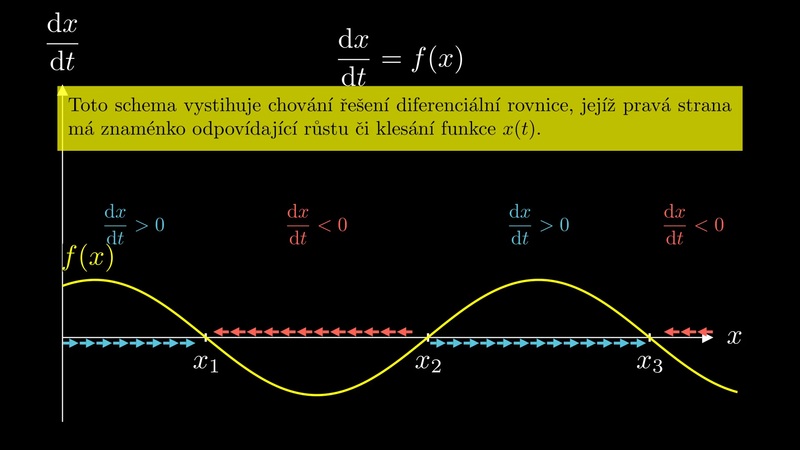
Autonomní diferenciální rovnice je rovnice tvaru
Všechna konstantní řešení rovnice (1) jsou nulové body pravé strany. Nazývají se stacionární body. Je užitečné umět posoudit chování řešení v okolí stacionárních bodů, což umožní následující věta.
Věta (stabilita konstantních řešení)
Jestliže platí \(\displaystyle f(y_0)=0\), je konstantní funkce \(\displaystyle y(t)=y_0\) konstantním řešením rovnice
Poznámka (stabilita řešení)
Stabilita je u diferenciálních rovnic chápána různým způsobem. V tomto textu stabilitou stacionárního bodu budeme rozumět, že malá výchylka od stacionárního bodu vede na řešení, které konverguje zpět k tomuto stacionárnímu bodu. Přesněji se tento typ stability jmenuje asymptotická stabilita.
Pro grafickou interpretaci věty je vhodné připomenout, že funkce s kladnou derivací jsou rostoucí a funkce se zápornou derivací klesající. Pokud má tedy pravá strana derivaci různou od nuly, poznáme stabilitu z monotonie pravé strany.
Věta je odvozena z pozorování, že rovnice \(\displaystyle y'=ky\) má řešení \(\displaystyle y(t)=Ce^{kt}\) a toto řešení se pro velká \(\displaystyle t\) blíží k nule nebo roste neohraničeně, v závislosti na znaménku hodnoty \(\displaystyle k\). Pravou stranu rovnice, funkci \(\displaystyle f(y)\), je možné aproximovat vztahem \(\displaystyle f(y)\approx f'(y_0)(y-y_0)\) a odsud a z poznatku, že malá změna rovnice většinou nemění dramaticky chování řešení (přesněji, existuje spojitá závislost na parametrech), a proto rovnice \(\displaystyle y'=f(y)\) kopíruje v okolí bodu \(\displaystyle y_0\) chování rovnice \(\displaystyle (y-y_0)'=f'(y_0)(y-y_0)\), pokud vynecháme patologické případy, což je zde \(\displaystyle f'(y_0)=0\). Řešení je tedy \(\displaystyle y\approx y_0+Ce^{f'(y_0)t}\) a tato funkce buď konverguje k \(\displaystyle y_0\), nebo roste neohraničeně, v závislosti na znaménku derivace \(\displaystyle f'(y_0)\).
10.1.1. Logistická diferenciální rovnice s konstantním lovem#
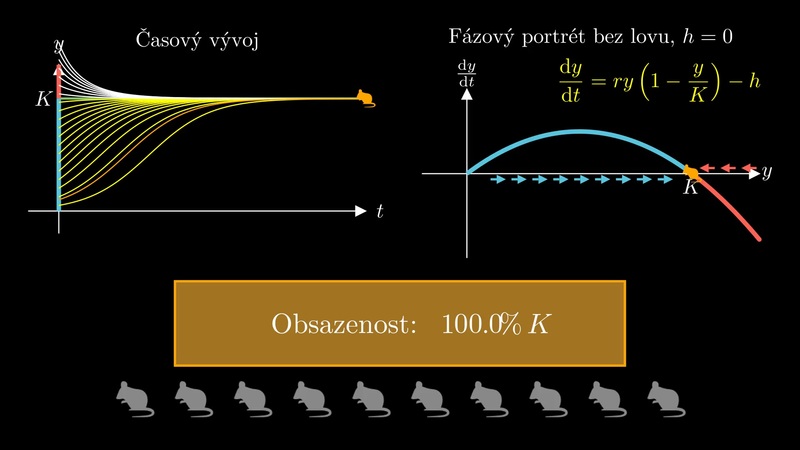
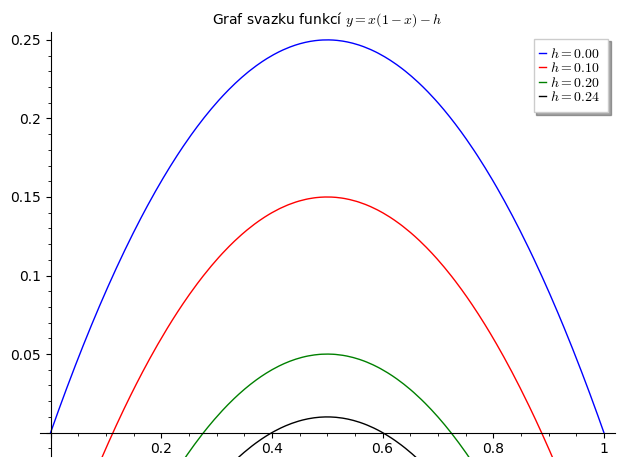
Obr. 10.1 Pravá strana k modelu lovu s konstantní intenzitou.#
Logistická diferenciální rovnice s konstantním lovem \(\displaystyle h\), tj. rovnice
Pokud se intenzita lovu zvětšuje tak, že se parabola dostane vrcholem na vodorovnou osu a poté pod tuto osu, oba stacionární body splynou v jeden a zaniknou. V okamžiku, kdy se vrchol dostává pod vodorovnou osu, i malinká změna v lovu způsobí dramatickou změnu v modelu. Ztratí se totiž existence stabilního řešení a všechna řešení budou konvergovat k nule.
Poznámka (strukturální stabilita modelu, bifurkace)
Stabilita je u diferenciálních rovnic chápána různým způsobem. V tomto textu budeme strukturální stabilitou modelu závislého na parametrech rozumět stav, kdy malá změna parametrů nemění kvalitativní vlastnosti rovnice nebo systému, tj. například zůstává stejný počet stacionárních bodů, zachovává se jejich stabilita. To je přirozené chování, kdy malá změna parametrů modelu způsobí malé změny v řešení. Pro některé hodnoty parametrů však strukturální stabilitu ztrácíme. V takovém případě se i při nepatrných změnách parametrů dramaticky mění chování rovnice nebo systému. Například při zvyšování lovu v právě uvažovaném modelu dva stacionární body splynou v jeden a zaniknou. Takové chování se nazývá bifurkace a hodnoty parametrů, při kterých k bifurkaci dojde, jsou důležité pro další vývoj předmětu. Zjednodušeně řečeno, malé změny parametrů v oblasti daleko od bifurkace znamenají, že chování modelu se mění pozvolna. Blízko k bifurkační hodnotě je situace komplikovanější a může se stát, že malá změna parametrů modelu způsobí dramaticky odlišné chování modelu. Rovnice blízká bifurkaci je citlivá na rozkolísání.
10.1.2. Model ostrovní biogeografie#
10.1.3. Model metapopulací#
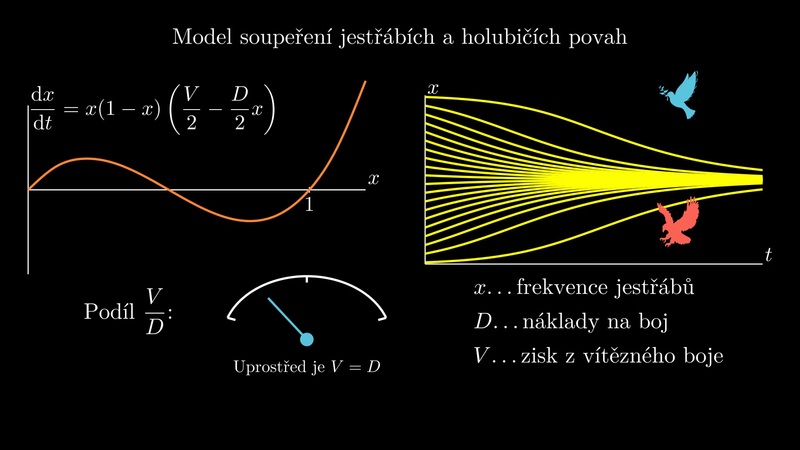
10.1.4. Model soupeření jestřábí a holubičí povahy#

Obr. 10.2 V modelu jestřáb-holubice (hawk-dove) nejde o skutečné živočišné druhy, ale o strategii chování. Předmětem modelu je jestřábí a holubičí povaha u jedinců téhož druhu. Zdroj: pixabay.com#
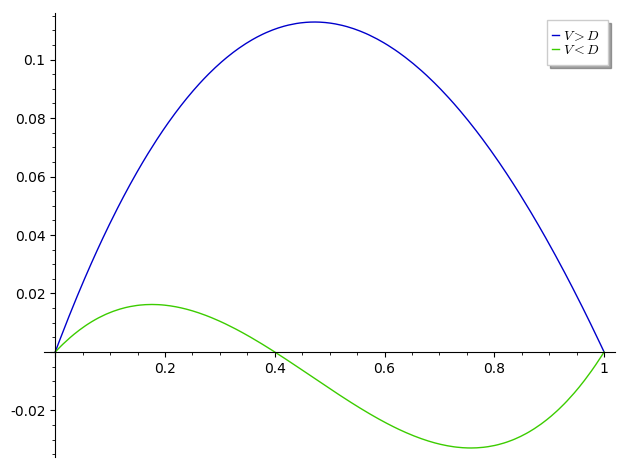
Obr. 10.3 Pravá strana modelu v závislosti na hodnotě parametrů.#
Cílem tohoto modelu je studovat typy chování živočichů a rostlin a zjistit, zda některý typ chování přináší jeho nositelům evoluční výhodu.
Nechť se v populaci vyskytují dva vzorce chování – jedince používající první z nich budeme nazývat jestřábi a druhý holubice. Chování se projeví, pokud se dva jedinci setkají u téhož zdroje (potrava, hnízdiště, apod).
Jestřáb o zdroj bojuje a ustoupí pouze po prohraném boji.
Holubice o zdroje nebojuje. Pokud protivník ustoupí bez boje, holubice zdroj zkonzumuje. V opačném případě zdroj zkonzumuje protivník.
Předpokládejme, že každý jedinec v populaci si zkonzumováním zdroje může svou evoluční zdatnost posílit o hodnotu \(\displaystyle V\). Pokud je nucen a ochoten o zdroj bojovat, je jeho evoluční zdatnost naopak snížena o hodnotu \(\displaystyle D\).
Setkají-li se u zdroje dvě holubice, jedna z nich ustoupí bez boje a druhá zkonzumuje zdroj. Předpokládejme, že po častých setkáních tohoto typu každá holubice zkonzumuje průměrně polovinu zdrojů.
Setká-li se u zdroje holubice s jestřábem, zkonzumuje celý zdroj jestřáb.
Setkají-li se u zdroje dva jestřábi, ani jeden z nich neustoupí a bojují o zdroj. Předpokládejme, že všichni jestřábi jsou stejně silní a po boji je pravděpodobnost zkonzumování zdroje poloviční pro každého jestřába.
Matematický rozbor (J. Kalas, Z. Pospíšil, Spojité modely v biologii) ukazuje, že četnost \(\displaystyle x\) výskytu jestřábů v populaci se řídí diferenciální rovnicí
V bodě \(\displaystyle x=0\) je funkce \(\displaystyle f\) nulová a rostoucí. Stacionární bod \(\displaystyle x=0\) je vždy nestabilní. Ať jsou tedy podmínky jakékoliv, vždy budou v populaci přítomni jestřábi. Přitom právě jestřábi paradoxně plýtvají zdroji energie na boj, namísto toho, aby celou energii zaměřili na rozmnožování. Z hlediska efektivity při využívání zdrojů prostředí platí, že populace složená ze samých holubic využívá zdroje prostředí nejefektivnějším možným způsobem. Přesto je taková populace evolučně nestabilní! Pronikne-li do populace samých holubic jeden jestřáb, má značnou evoluční výhodu, protože každý zdroj, u kterého se nachází, zkonzumuje. Tím poroste jeho evoluční zdatnost a jeho geny nebo vzorce chování (u druhů, které mohou přepínat strategie chování) se budou v populaci rychle šířit.
Pokud jsou náklady na boj větší než užitek ze zdrojů, platí \(\displaystyle V<D\). V intervalu \(\displaystyle [0,1]\) leží stacionární bod \(\displaystyle x=\frac VD\) a tento bod je stabilní. Poslední stacionární bod \(\displaystyle x=1\) je nestabilní. V tomto případě všechna řešení konvergují ke stacionárnímu bodu \(\displaystyle x=\frac VD\). V populaci tedy budou přítomni i jestřábi i holubice.
Pokud platí \(\displaystyle V>D\), všechna řešení konvergují ke stacionárnímu bodu \(\displaystyle x=1\). Ať je počáteční rozložení vzorců chování v populaci jakékoliv, evolučně stabilní je pouze populace složená ze samých jestřábů. Jsou-li náklady na boj o zdroje nižší než užitek ze zdrojů, nevyplatí se ustupovat při soupeření o zdroje. Příkladem populace složené ze samých jestřábů je les. Náklady na boj spočívají ve vytvoření vyššího kmene, užitkem je světlo.
10.2. Autonomní rovnice s pravou stranou ve tvaru rozdílu#
Poznámka (autonomní rovnice s rozdílem na pravé straně)
Rovnice
10.2.1. Teplotní bilance Země#
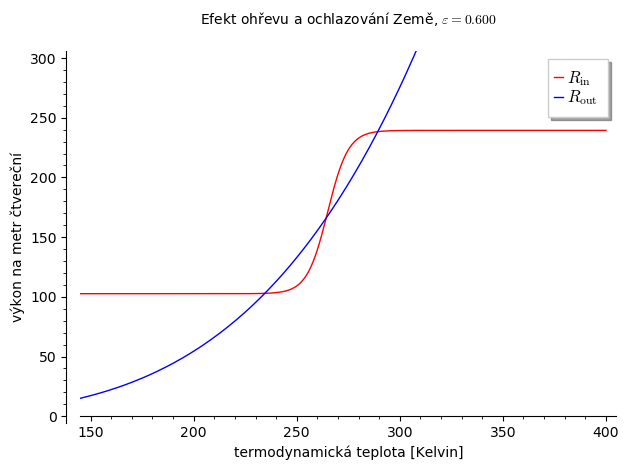
Obr. 10.4 Funkce z pravé strany rovnice pro teplotní bilanci Země#
Příklad. Teplotní bilanci Země je možno vyjádřit rovnicí
10.2.2. Logistická diferenciální rovnice s predátory#


Obr. 10.5 Model obaleče byl publikován v D. Ludwig, D.D. Jones and C.S. Holling, Qualitative analysis of insect outbreak systems: the spruce budworm and forest, Journal of Animal Ecology 47(1): 315–332, February 1978 a v tomto odstavci je zpracován podle knihy Brauer, Kribs, Dynamical systems for biological modelling, plný text je pro uživatele MENDELU zdarma. zdroj: Wikimedia.org#
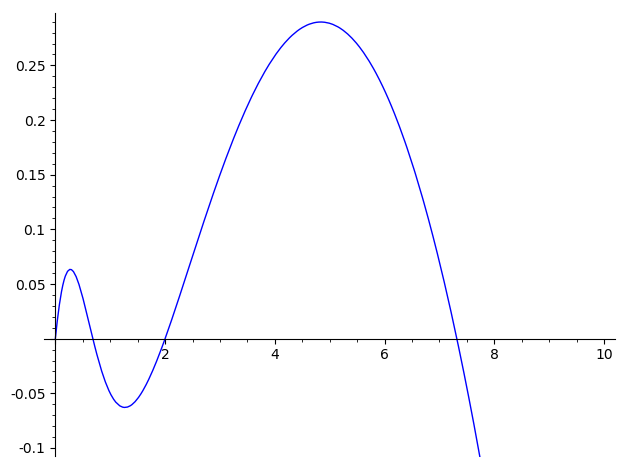
Obr. 10.6 Pravá strana diferenciální rovnice modelu obaleče jako funkce proměnné \(\displaystyle y\).#
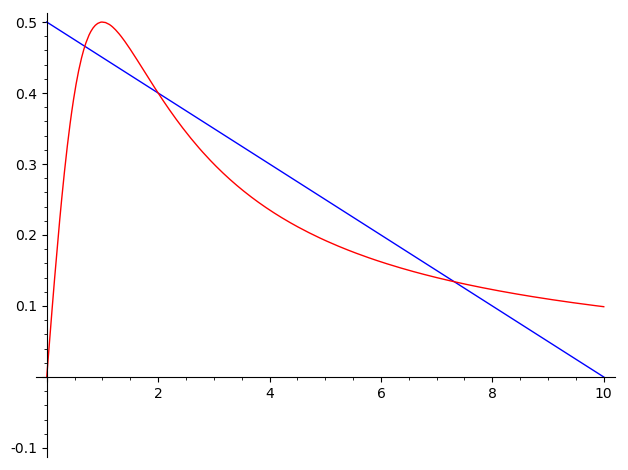
Obr. 10.7 Křivky udávající znaménko pravé strany diferenciální rovnice z modelu obaleče.#
Následující model je model obaleče Choristoneura fumiferana, který periodicky atakuje lesy severní Ameriky. Jeho populace je relativně malá, ale některé roky (historicky cca po 40 letech) se velikost populace zvýší tisícinásobně a dokáže zahubit \(\displaystyle 80\%\) stromů v lese a prakticky zničit les. Populaci je možno modelovat logistickou rovnicí
Vidíme dva průsečíky, kde je funkce rostoucí, to odpovídá nestabilním stavům. Vidíme i dva stabilní stavy, přibližně pro hodnoty \(\displaystyle 0.6\) a \(\displaystyle 7.3\). Malé populace, které se rozvíjejí od nuly, dospějí do nižšího stabilního stavu. Pokud se nějakým způsobem změní velikost populace o malé množství, systém se po čase díky stabilitě vrátí do původního stavu. Pokud však skok je velký a systém populace se dostane nad hodnotu nestabilního stavu, růst pokračuje a systém spěje ke stabilitě, ale s vyšším výskytem škůdce, který odpovídá stacionárnímu bodu \(\displaystyle 7.3\).
Poněkud jednodušší je kvalitativní analýza, pokud vhodně zvolíme jednotku času a jednotku veličiny \(\displaystyle y\). Jednotku veličiny \(\displaystyle y\) zvolíme tak, aby koeficient \(\displaystyle A\) byl roven jedné. Jednotku času zvolíme tak, aby koeficient \(\displaystyle H\) byl roven jedné. Kromě toho vytkneme proměnnou \(\displaystyle y\). Model má potom tvar
Brauer a Kirbs vysvětlují situaci tak, že s růstem lesa se mění parametry modelu, stacionární body se posunují a populace obaleče se tomu přizpůsobuje. Více stromů znamená vyšší nosnou kapacitu prostředí pro obaleče a predátoři svou činností populaci obaleče udržují na rozumné míře. Pokud však nosná kapacita prostředí dosáhne takové hodnoty, že predátoři jsou nasycení a nestačí populaci redukovat, odpovídá to posunu nestabilního stacionárního bodu pod hodnotu velikosti populace a dojde k přemnožení. Toto přemnožení má devastující účinky pro les.
10.3. Autonomní systém \(\displaystyle X'=f(X)\)#
Soustava diferenciálních rovnic, kde pravé strany nezávisí na čase, se nazývá autonomní systém. Seznámili jsme se již s lineárními autonomními systémy, obecný autonomní systém však lineární být nemusí. Například při modelování chemických reakcí je rychlost úměrná mocnině koncentrace reagujících látek odpovídající počtu molekul, které do reakce vstupují. Níže uvidíme příklad takového modelu.
Ukážeme si, jak studovat nelineární systém pomocí lineárního a pomocí vlastních čísel. Půjde o lineární aproximaci. V tomto případě o lineární aproximaci vektorové funkce definující pravé strany rovnic.
Je-li \(\displaystyle f(X_0)=0\), je možno systém
Zejména tedy, pokud má Jacobiho matice všechny vlastní hodnoty záporné, tak všechna řešení z nějakého okolí stacionárního bodu konvergují do tohoto bodu. Pokud má všechny vlastní hodnoty kladné, všechna řešení z nějakého okolí se naopak od stacionárního bodu vzdalují. To platí i pro komplexní vlastní hodnoty, pouze se mezi konvergencí a vzdalováním přepíná podle znaménka reálné části vlastních hodnot a řešení oscilují směrem ke stacionárnímu bodu nebo od něj.
Poznámka (stabilita a strukturální stabilita řešení)
Stabilitou stacionárního bodu budeme rozumět, stejně jako výše, že malá výchylka od stacionárního bodu vede na řešení, které konverguje zpět k tomuto stacionárnímu bodu. Stabilita vyjadřující, že při malé změně koeficientů v systému se nezmění typ singulárních bodů, se nazývá strukturální stabilita.
10.3.1. Bruselátor#
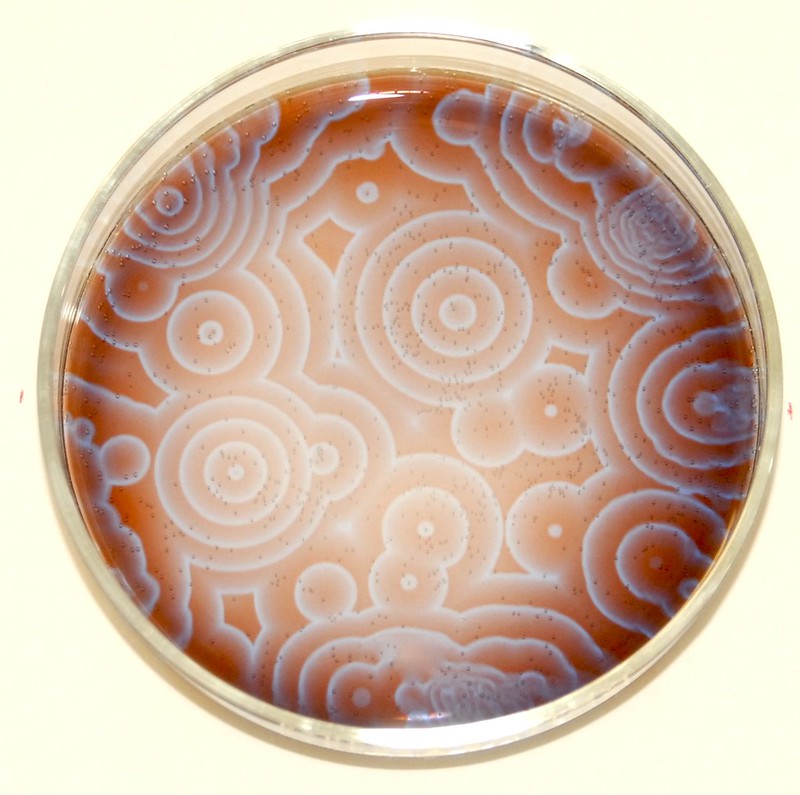
Obr. 10.8 Bělousova-Žabotinského reakce vytváří periodicky se měnící obrazce. Autor: Stephen Morris, flickr.com#
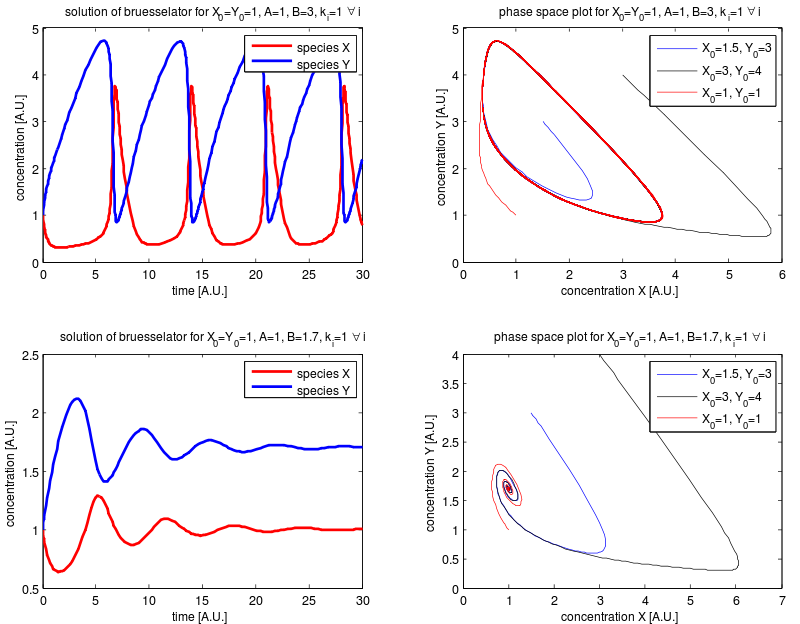
Obr. 10.9 Fázový portrét brusselátoru. Zdroj: Wikipedia#
Systém chemických reakcí
Pokud je dostatek složek \(\displaystyle A\) a \(\displaystyle B\), modeluje po zjednodušení (viz Wikipedie, konstanty úměrnosti klademe rovny jedné) chemické reakce soustava
Stacionárním bodem je bod \(\displaystyle X=A\), \(\displaystyle Y=\frac BA\). Pro \(\displaystyle A=1\) a \(\displaystyle B=3\) má systém tvar
Jacobiho matice je
10.4. Autonomní systém ve dvou dimenzích#
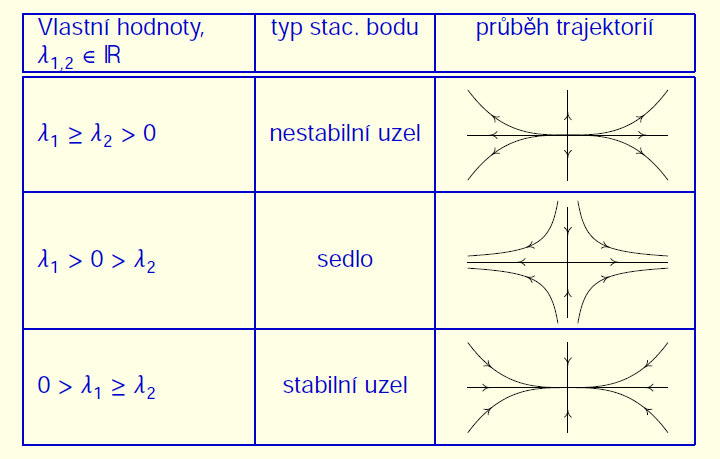
Obr. 10.10 Trajektorie pro stacionární body spojené s reálnými vlastními čísly.#
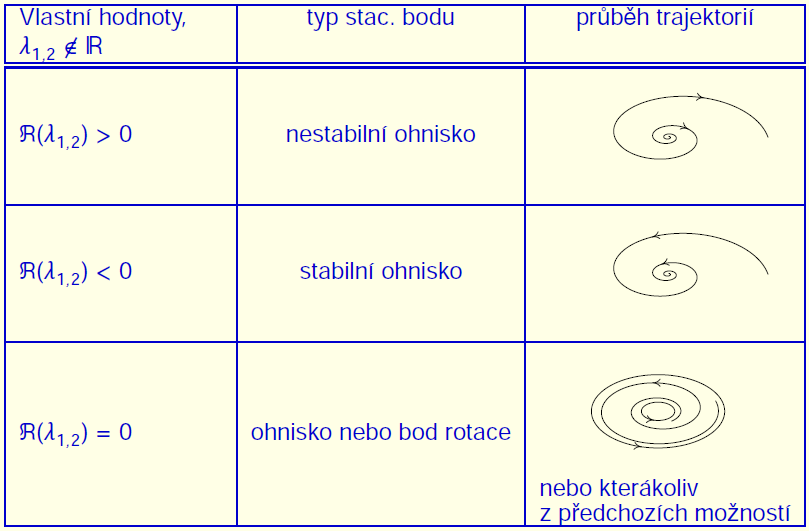
Obr. 10.11 Trajektorie pro stacionární body spojené s nereálnými vlastními čísly.#
Ve dvou dimenzích je autonomní systém možno psát ve tvaru
Řešení zobrazíme jako grafy funkcí \(\displaystyle x(t)\) a \(\displaystyle y(t)\). Tímto přístupem dokážeme posoudit dynamiku v čase, odhadnout rychlost, s jakou se mění obě komponenty řešení. Často kreslíme do jednoho obrázku a často máme v tomto obrázku dvojí souřadnicový systém: jeden pro hodnoty \(\displaystyle x\) a jeden pro hodnoty \(\displaystyle y\).
Řešení zobrazíme jako parametrickou křivku \(\displaystyle \vec r(t)=[x(t), y(t)]\). Tato křivka se nazývá trajektorie. V tomto případě sice nemáme informaci o dynamice v čase, ale můžeme lehce posoudit, jak se chovají řešení vycházející z různých počátečních podmínek. Proto tento způsob zpravidla preferujeme. Tento způsob znázornění se nazývá fázový portrét.
Křivky tvořené trajektoriemi mají speciální vlastnosti. Například se díky jednoznačné řešitelnosti nemohou dvě různé trajektorie protnout. Díky tomu existuje jenom několik málo druhů trajektorií.
Stacionární body. Tyto body odpovídají konstantním řešením.
Uzavřené trajektorie, cykly. Tyto trajektorie odpovídají periodickým řešením. Uvnitř každého cyklu leží alespoň jeden stacionární bod.
Trajektorie, které samy sebe nikde neprotínají, a pro \(\displaystyle t\to\pm\infty\) tyto trajektorie mají jednu z následujících vlastností.
Trajektorie mají alespoň jednu složku neohraničenou.
Trajektorie konvergují k některému ze stacionárních bodů.
Trajektorie konvergují k některému z cyklů.
Trajektorie konvergují k množině tvořené konečným počtem singulárních bodů a jinými trajektoriemi, které vedou z jednoho stacionárního bodu do druhého. S tímto typem trajektorií se však v jednoduchých modelech nesetkáme.
Podle chování trajektorií v okolí stacionárních bodů rozdělujeme tyto stacionární body do několika navzájem disjunktních skupin. Dokážeme je identifikovat pomocí vlastních hodnot Jacobiho matice vypočtené v tomto stacionárním bodě.
Stabilní uzel je stacionární bod takový, že pro \(\displaystyle t\to\infty\) všechny trajektorie z nějakého okolí konvergují do tohoto bodu bez oscilací. Nestabilní uzel má stejnou vlastnost, ale pro \(\displaystyle t\to-\infty\), tedy trajektorie z tohoto bodu vycházejí. Stabilní uzel poznáme podle dvou záporných a nestabilní uzel podle dvou kladných reálných vlastních hodnot.
Stabilní a nestabilní ohnisko je stacionární bod se stejnou vlastností jako uzel, ale konvergence je spojena s oscilacemi okolo stacionárního bodu. Stabilní ohnisko poznáme podle dvou komplexně sdružených vlastních hodnot se zápornou reálnou částí, nestabilní ohnisko s kladnou reálnou částí.
Sedlo je stacionární bod, který má v každém okolí pouze konečný počet trajektorií, které pro \(\displaystyle t\to\pm\infty\) konvergují k tomuto bodu. Poznáme jej podle jedné kladné a jedné záporné vlastní hodnoty.
Bod rotace je takový bod, v jehož každém okolí jsou cykly. Pokud navíc v nějakém okolí existují pouze cykly, nazývá se tento bod navíc střed. Bod rotace souvisí s komplexně sdruženými vlastními čísly s nulovou reálnou částí, ale v těchto případech může stacionární bod být i ohniskem.
10.5. Základní modely populační ekologie#
Populační ekologie je součást ekologie zabývající se modelováním vývoje populací. Základním vyjadřovacím jazykem jsou diferenciální rovnice nebo jejich diskrétní obdoba, kdy se čas mění po skocích, diferenční rovnice. Málokdy uvažujeme jedinou populaci, většinou studujeme bohatší ekosystémy, což vede na soustavy rovnic. Dva nejklasičtější příklady si zde stručně uvedeme a prostudujeme ve cvičení.
10.5.1. Model konkurence dvou druhů#
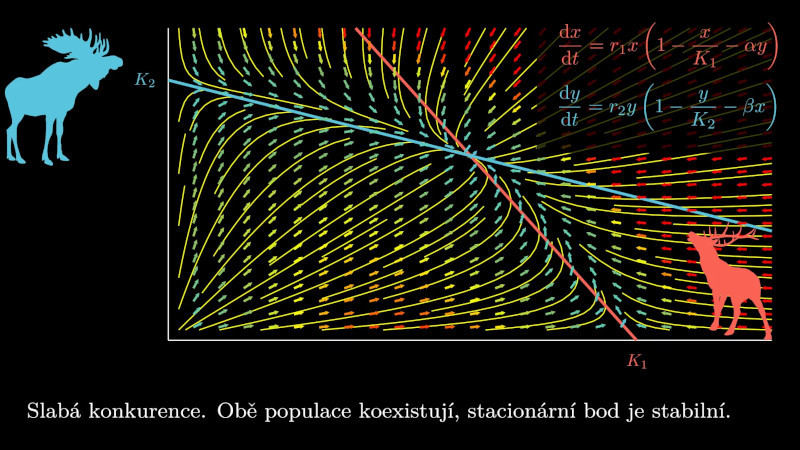
Situace, kdy dva druhy žijí ve společné lokalitě a přítomnost jednoho druhu ovlivňuje druhý druh, je modelována autonomním systémem
10.5.2. Model dravce a kořisti#
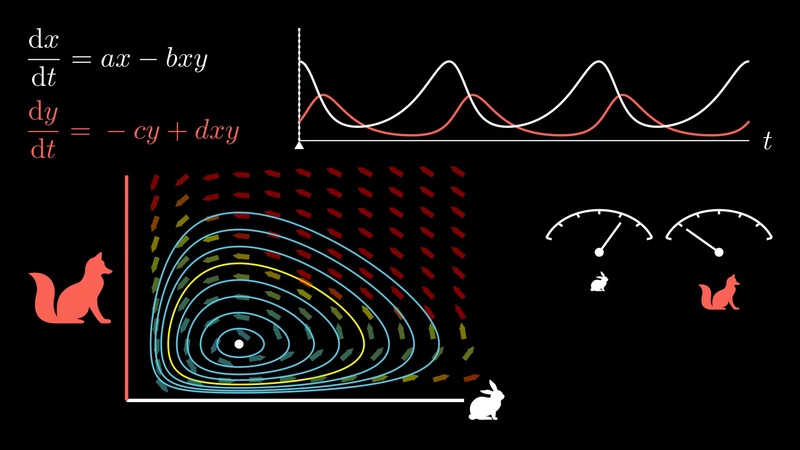
Situace, kdy dva druhy žijí ve společné lokalitě a přítomnost jednoho druhu umožňuje přežití druhého, je modelována autonomním systémem
10.6. Vícerozměrné autonomní systémy, kompartmentové modely#
Kompartmentové modely jsou modely, kde se je studovaná veličina rozdělena do několika stavů a mezi těmito stavy se v jakémsi smyslu přelévá definovanou rychlostí. Klasickým případem v roce 2020 je model epidemie, například SIR model nebo SEIR model.