6. Dvojný integrál#
Anotace
V předchozí přednášce jsme si ukázali rozšíření integrálu, které nám umožnilo počítat integrál nejenom po úsečce, ale i po libovolné křivce. V této přednášce se naučíme integrovat přes dvourozměrný obrazec v rovině. Seznámíme se s dvojným integrálem.
Mezi aplikace spadá střední hodnota na dvourozměrné oblasti.
Pomocí dvojného integrálu je definován kvadratický moment průřezu nosníku, což je zásadní veličina ovlivňující tuhost a chování těchto nosníků při deformaci.
Pomocí dvojného integrálu je možné určit množství veličiny ze znalosti její plošné hustoty. To využijeme později při makroskopické formulaci bilance stavové veličiny a při odvození difuzní rovnice v integrálním tvaru.
Prerekvizity
Dvojný integrál počítáme převodem na dva jednorozměrné Riemannovy integrály. Je proto tedy dobré ovládat výpočet neurčitého a určitého Riemannova integrálu.
V praxi pracujeme s řadou veličin, které se počítají tak, že se parametr systému násobí obsahem.
Z plošné hustoty desky a jejího obsahu násobením obdržíme hmotnost desky.
Z hloubky nádrže (se svislými stěnami) a obsahu hladiny obdržíme násobením objem.
Z tlaku a obsahu stěny obdržíme násobením tlakovou sílu působící na stěnu nádrže.
Je však otázka, jak tento přístup použít v případě, že daný parametr není po celé ploše konstantní. Deska může být nehomogenní, nádrž nemusí mít vodorovné dno a tlak působící na stěnu nádrže není ve všech místech stejný, protože různé části stěny jsou v různé hloubce.
U křivkového integrálu jsme se setkali s momentem setrvačnosti. Ukázali jsme si, jak stanovit moment setrvačnosti množiny, která má hmotnost rozloženu na křivce a třeba i nerovnoměrně. Při výpočtu namáhání nosníků, trámů, polic nebo stromů řešíme podobnou úlohu, ale pro množiny v rovině namísto křivek. Potřebujeme zohlednit, že při deformaci nosníků se pro jednotlivé body průřezu liší vzdálenost od neutrální osy.
Řešení uvedených nesnází je stejné: další rozšíření integrálního počtu a zavedení dvojného integrálu. Ten si nyní představíme.
6.1. Motivace 1 (hmotnost nehomogenní desky)#

Obr. 6.1 Deska s nekonstantní plošnou hustotou. Zdroj: https://www.flickr.com/photos/svacher, licence CC BY-NC-ND 2.0#
Hmotnost \(\displaystyle m\) desky \(\displaystyle \Omega\) je možno vypočítat jako součin plošné hustoty \(\displaystyle \sigma\) (hmotnost na jednotku obsahu) a obsahu \(\displaystyle S\) desky podle vzorce
\[m=\sigma S.\]Toto funguje pro desky s konstantní plošnou hustotou, kdy má deska ve všech místech stejné fyzikální vlastnostmi.
Pokud je deska slepená z konečného počtu malých homogenních desek o různých plošných hustotách, určíme hmotnost každé jednotlivé desky samostatně a výsledky potom sečteme.
\[m=\sigma_1 S_1+\sigma_2 S_2+\cdots + \sigma_n S_n\]Pokud není možné nebo vhodné použít předchozí bod, musíme předpokládat, že hustota je obecnou funkcí. Potom namísto součtu konečného počtu sčítanců následuje nekonečný počet sčítanců a vybudujeme aparát, který nám umožní psát
\[m=\iint_\Omega \sigma \,\mathrm dS.\]
6.2. Motivace 2 (objem vody v jezeře)#

Obr. 6.2 Nádrž s proměnnou hloubkou. Zdroj: https://www.pixabay.com#
Objem vody \(\displaystyle V\) v nádrži nebo bazénu (se svislými stěnami, ale jinak i nepravidelného půdorysu \(\displaystyle \Omega\)) vypočteme jako součin obsahu hladiny \(\displaystyle S\) a hloubky vody \(\displaystyle h\) podle vzorce
\[V=Sh.\]To ovšem platí jenom, pokud je v každém místě stejná hloubka.Pokud má jedna část bazénu jinou hloubku než část druhá, vypočteme objem u každé hloubky samostatně a příspěvky sečteme. Objem je tedy dán vztahem
\[V=S_1h_1+S_2h_2.\]Předchozí postup je možné aplikovat pro konečně mnoho hloubek, ale někdy to je nevhodné nebo, v případě spojitě se měnící hloubky, dokonce nemožné. Potom místo součtu konečně mnoha příspěvků použijeme dvojný integrál a dostáváme
\[V=\iint_\Omega h\mathrm dS.\]
6.3. Motivace 3 (průtok)#

Obr. 6.3 Průtok potrubím je ovlivněn tím, že u stěny teče tekutina pomaleji než ve středu, potrubí na Aljašce. Zdroj: https://www.pixabay.com#
Teče-li průřezem \(\displaystyle \Omega\) tekutina kolmo na průřez rychlostí \(\displaystyle v\), je celkový průtok \(\displaystyle Q\) (objem, který proteče průřezem za jednotku času) dán součinem
\[Q=vS,\]kde \(\displaystyle S\) je plošný obsah průřezu.Teče-li různými místy průřezu voda různou rychlostí, sečteme jednotlivé příspěvky podle vzorce
\[Q=v_1S_1+v_2S_2+\dots +v_nS_n.\]Myšlenku z předchozího bodu není snadné udělat, pokud se rychlost mění spojitě. Například v potrubí je rychlost rozdělena parabolicky a ubývá se vzdáleností od středu. Situaci zachraňuje dvojný integrál
\[Q=\iint_\Omega v\,\mathrm dS.\]
6.4. Dvojný integrál#
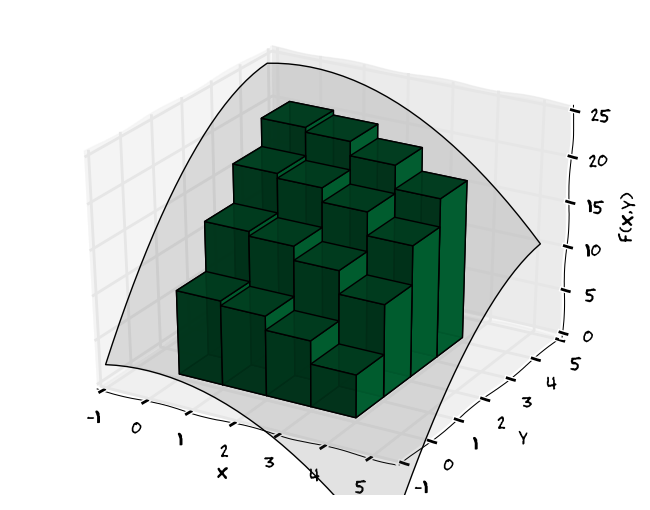
Pro dvojný integrál použijeme podobnou myšlenkovou konstrukci jako u křivkového integrálu prvního druhu, pouze místo drátu s danou lineární hustotou budeme uvažovat rovinnou ohraničenou desku s danou plošnou hustotou.
Pokud je hustota desky konstantní, je možno její hmotnost získat jednoduše jako součin plošné hustoty a obsahu.
Pokud se hustota desky mění a v obecném bodě \(\displaystyle (x,y)\) je dána funkcí \(\displaystyle f(x,y)\), můžeme myšlenkově rozdělit desku na malé kousky, v rámci každého malého kousku hustotu aproximovat konstantou, vypočítat hmotnost každého kousku jako součin hustoty a obsahu a všechny hmotnosti sečíst.
Získaná veličina je aproximací celkové hmotnosti.
V limitním přechodu kdy rozměry všech kousků na něž je deska dělena jdou k nule dostáváme dvojný integrál
6.5. Linearita a aditivita#
Dvojný integrál je odvozen (tak jako všechny integrály) pro aditivní veličiny a proto se „dobře snáší“ se sčítáním (ať už integrovaných funkcí, nebo integračních oborů) a s násobení integrované funkce konstantou. Přesněji, platí následující věty.
Věta (linearita dvojného integrálu)
Buď \(\displaystyle f_1\), \(\displaystyle f_2\) funkce integrovatelné v \(\displaystyle \Omega\) a \(\displaystyle c_1\), \(\displaystyle c_2\) libovolná reálná čísla. Platí
Věta (aditivita vzhledem k oboru integrace)
Nechť je množina \(\displaystyle \Omega\) rozdělena na dvě oblasti \(\displaystyle \Omega_1\) a \(\displaystyle \Omega_2\), které mají společné nejvýše hraniční body. Platí
6.6. Výpočet dvojného integrálu#
Výpočet dvojného integrálu se provádí převodem, na integrály funkcí jedné proměnné.
6.6.1. Výpočet (oblast mezi funkcemi proměnné \(\displaystyle x\))#
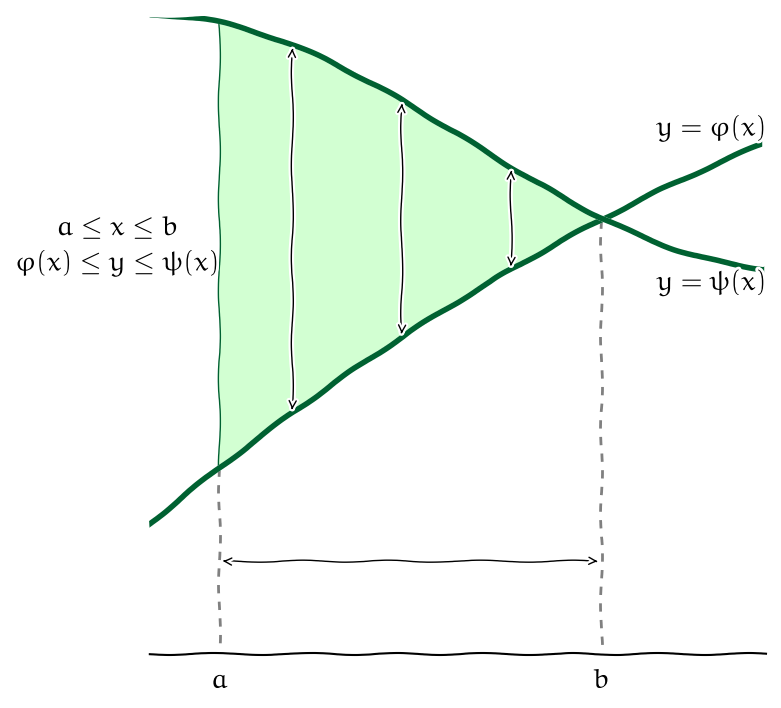
Obr. 6.4 Oblast mezi funkcemi proměnné \(\displaystyle x\).#
V závislosti na tom, jakými nerovnostmi množinu \(\displaystyle \Omega\) definujeme, můžeme pro výpočet dvojného integrálu použít následující věty. Tyto věty udávají, jak je možno dvojný integrál přepsat jako dvojnásobný integrál. Mají název Fubiniovy věty.
Věta (Fubiniova věta)
Nechť \(\displaystyle f\) je funkce spojitá v uzavřené oblasti
6.6.2. Výpočet (oblast mezi funkcemi proměnné \(\displaystyle y\))#
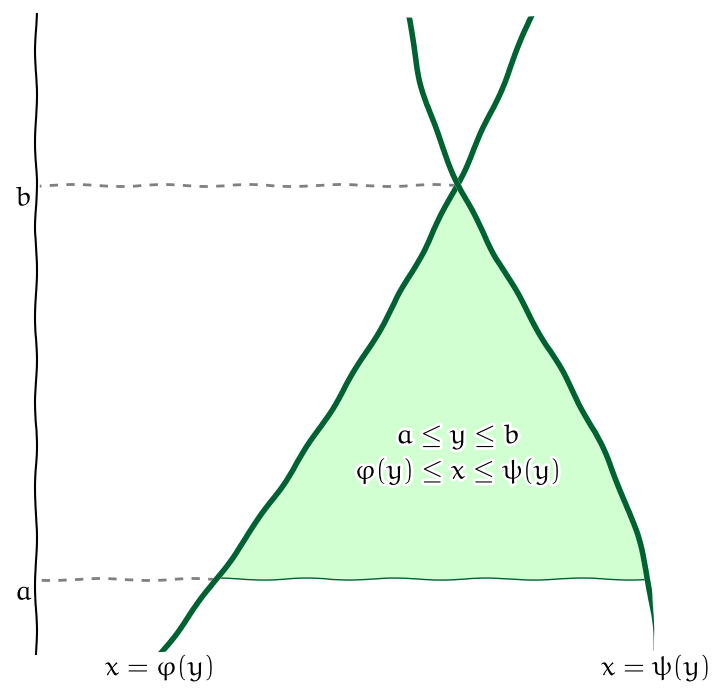
Obr. 6.5 Oblast mezi funkcemi proměnné \(\displaystyle y\).#
Věta (Fubiniova věta pro jiné pořadí integrace)
Nechť \(\displaystyle f\) je funkce spojitá v uzavřené oblasti
6.6.3. Záměna pořadí integrace#
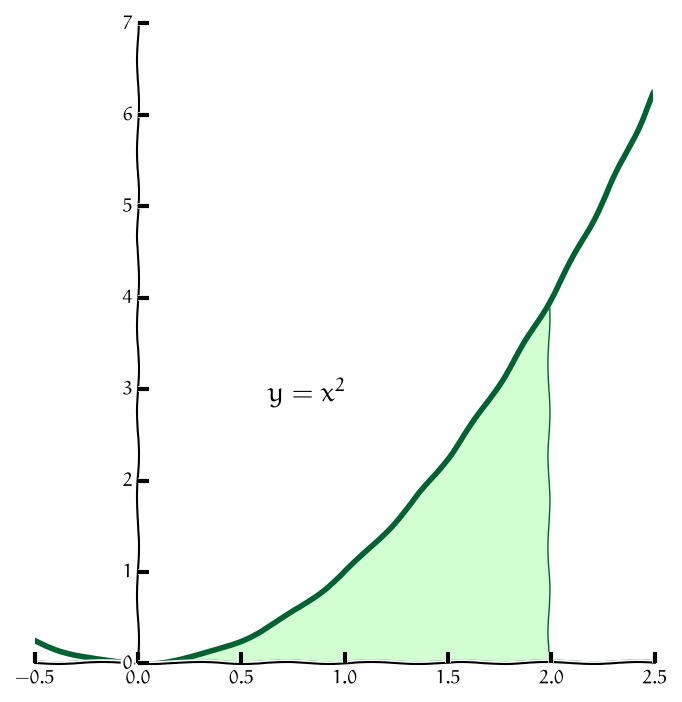
Obr. 6.6 Oblast, pro kterou jsou možná obě pořadí integrace.#
Často je možné oblast integrace zapsat pomocí obou možností uvedených na předchozích slidech. Například oblast na obrázku je možno zapsat buď jako
Pro integrál funkce \(\displaystyle f(x,y)\) přes takovou množinu tedy máme dvě alternativy. Buď
Všimněte si, že nestačí prosté prohození integrálů. Je nutno přepočítávat meze a hraniční křivky je nutno vyjádřit jednou jako funkce proměnné \(\displaystyle x\) a jednou jako funkce proměnné \(\displaystyle y\). V důsledku tohoto dochází v průběhu výpočtu dvěma různými způsoby k tomu, že pracujeme se dvěma různými integrály. Výsledky jsou samozřejmě stejné, ale nemusí být dosažitelné srovnatelnou námahou. Jedna z cest může být snazší.
6.7. Výpočet (obdélníková oblast)#
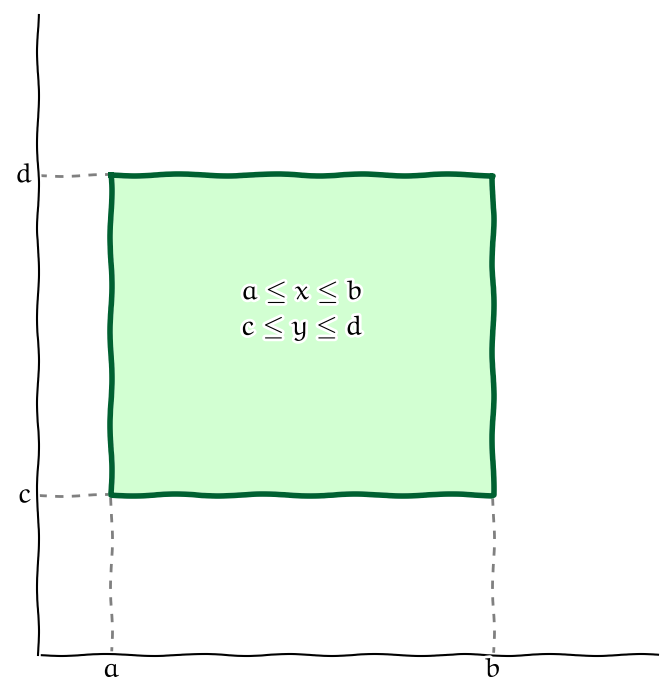
Obr. 6.7 Integrál přes obdélník.#
Výše uvedené problémy se stanovením a případným přepočítáváním mezí při záměně pořadí integrace se nevyskytují při integrování přes obdélníkovou oblast.
Věta (Fubiniova věta na obdélníku)
Nechť \(\displaystyle R=[a,b]\times[c,d]\) je uzavřený obdélník v \(\displaystyle \mathbb{R}^2\) a \(\displaystyle f\) funkce definovaná a spojitá na \(\displaystyle R\). Pak platí
Platí-li dokonce rovnost \(\displaystyle f(x,y)=g(x)h(y)\), pak
6.8. Aplikace dvojného integrálu#
6.8.1. Matematické aplikace dvojného integrálu#
Obsah \(\displaystyle \mu(\Omega)\) množiny \(\displaystyle \Omega\) vypočteme jako integrál
\[\mu(\Omega)=\iint_\Omega \mathrm{d}x \mathrm{d}y.\]Integrální střední hodnota funkce \(\displaystyle f(x,y)\) definované na množině \(\displaystyle \Omega\) je
\[ \frac{\iint_\Omega f(x,y)\mathrm{d}x \mathrm{d}y }{\mu (\Omega)},\]kde \(\displaystyle \mu (\Omega)=\iint_\Omega\mathrm{d}x\mathrm{d}y\) je obsah množiny \(\displaystyle \Omega\).
6.8.2. Objem kopce nebo jezera pomocí vrstevnic#

Obr. 6.8 Posvátná hora Japonska. Objem se dá určit pomocí obsahů vrstevnic. Zdroj: https://www.pixabay.com#
Obsah množiny ohraničené vrstevnicí na mapě vynásobený rozestupem mezi vrstevnicemi je přibližně roven objemu vrstvy mezi dvěma vrstevnicemi.
Pokud sečteme obsahy všech vrstevnic a vynásobíme rozestupem mezi těmito vrstevnicemi, dostaneme odhad pro objem kopce. Vlastně je to jako bychom kopec rozřezali na stejně tlusté plátky, naskládali je vedle sebe, sečetli obsahy postav takto vzniklých těles a vynásobili výškou.
Podobně je možné odhadnout objem jezera.
V tomto případě je dvojný integrál pouze koncept. Samozřejmě nemáme ambice vyjadřovat vrstevnice v analytickém tvaru a integrovat pomocí Fubiniovy věty. Ke slovu přijde spíše numerický výpočet integrálu.
6.8.3. Fyzikální aplikace dvojného integrálu#
Hmotnost množiny \(\displaystyle M\) je
\[m=\iint_M \sigma(x,y)\mathrm{d}x \mathrm{d}y,\]kde \(\displaystyle \sigma(x,y)\) je plošná hustota (hmotnost vztažená na jednotku povrchu).Je-li plošná \(\displaystyle u\) hustota kinetické energie molekul (což je veličina úměrná termodynamické teplotě), je \(\displaystyle \iint_M u\,\mathrm dx\mathrm dy\) celková kinetická energie částic. Tato energie se může měnit tepelnou výměnou. Rychlost, s jakou se mění část vnitřní energie související s teplotou, je
\[\frac{\mathrm d}{\mathrm d t}\left(\iint_M u\,\mathrm dx\mathrm dy\right)\]a odsud odvozujeme rovnici vedení tepla.Lineární momenty hmotné množiny \(\displaystyle M\) vzhledem k osám \(\displaystyle y\) a \(\displaystyle x\) jsou rovny
\[\iint_M x\sigma(x,y)\mathrm{d}x \mathrm{d}y\]a\[\iint_M y\sigma(x,y)\mathrm{d}x \mathrm{d}y.\]Moment setrvačnosti hmotné množiny \(\displaystyle M\) vzhledem k ose je
\[J=\iint_M \rho^2(x,y)\sigma(x,y)\mathrm{d}x \mathrm{d}y ,\]kde \(\displaystyle \rho(x,y)\) je vzdálenost bodu \(\displaystyle (x,y)\) od osy otáčení. Například pro osu \(\displaystyle x\) je \(\displaystyle \rho(x,y)=y\) a pro osu \(\displaystyle y\) je \(\displaystyle \rho (x,y)=x\). Pro osu procházející kolmo počátkem je \(\displaystyle \rho(x,y)=\sqrt{x^2+y^2}\).
6.8.4. Technické aplikace dvojného integrálu#

Obr. 6.9 Dřevostavba realizovaná pomocí I-nosníků. I-nosníky mají vysoký kvadratický moment při nízké spotřebě materiálu. Proto jsou tuhé a silné i při nízké hmotnosti. Ve strojařině se používají odedávna, první dřevostavba z nosníků tohoto typu byla v ČR realizována 2011. Zdroj: https://www.taus.eu#

Obr. 6.10 Větrné turbíny jsou konstruovány podobně jako I nosníky, pevný materiál na vnějších stranách a materiál s menší pevností uvnitř. Například balzové dřevo. A podobně jsou „konstruovány“ například listy rostlin. Zdroj: pixabay.com, tpsdave#

Souřadnice těžiště množiny jsou podílem lineárních momentů a celkové hmotnosti množiny.
Kvadratický moment průřezu (což je moment setrvačnosti pro \(\displaystyle \sigma(x,y)=1\), anglicky second moment of area) je veličina, která hraje podstatnou roli v mechanice (nábytek, stavby) při dimenzování (polic, nosných tyčí, nosníků).
V technické praxi zpravidla neuvažujeme nekonstantní plošnou hustotu. Potom je možné je bez újmy na obecnosti nahradit jedničkou. Vzorce pro obsah, \(\displaystyle x\)-ovou souřadnici těžiště (\(\displaystyle x_0\)), \(\displaystyle y\)-ovou souřadnici těžiště (\(\displaystyle y_0\)), kvadratický moment vzhledem k ose \(\displaystyle x\) (\(\displaystyle I_x\)) a kvadratický moment vzhledem k ose \(\displaystyle y\) (\(\displaystyle I_y\)) (pro množinu \(\displaystyle M\) s plošnou hustotou \(\displaystyle 1\)) jsou
\[\begin{split} \begin{alignedat}{2} % S&=\iint_M\mathrm{d}x \mathrm{d}y \\ x_0&=\frac 1S \iint_M x\mathrm{d}x \mathrm{d}y ,&\qquad I_x&= \iint_M y^2\mathrm{d}x \mathrm{d}y, \\ y_0&=\frac 1S \iint_M y\mathrm{d}x \mathrm{d}y , & I_y&= \iint_M x^2\mathrm{d}x \mathrm{d}y, \\ \end{alignedat} \end{split}\]kde \(\displaystyle S=\mu (M)\) je obsah množiny \(\displaystyle M\). Poloha těžiště je tedy střední hodnotou funkcí \(\displaystyle x\) a \(\displaystyle y\).
6.8.5. Tuhost nosníků, stabilita stromů#

Obr. 6.11 Tuhost a nosnost nosníků nebo podpěr souvisí s kvadratickým momentem průřezu. Zdroj: pixabay.com#

Obr. 6.12 Poloviční poloměr znamená u homogenního materiálu šestnáctkrát menší tuhost. Tedy jenom šest procent původní tuhosti! U stromu je tento poměr ještě horší díky různým druhům dřeva uprostřed a na kraji. Vánoční strom pro Prahu na Vánoce 2019. Zdroj: Taiko, Pražský deník#
Tuhost (odolnost vůči deformaci) pro nosník obdélníkového průřezu o výšce \(\displaystyle b\) a šířce \(\displaystyle a\) je dána kvadratickým momentem obdélníkového průřezu vzhledem k vodorovné ose procházející těžištěm.
Pokud šířka vzroste dvakrát, tuhost vzroste také dvakrát. Pokud ale dvakrát vzroste výška, tuhost vzroste dokonce osmkrát. Pro nosník s poměrem stran 1:2 je poměr tuhostí při poloze naplacato a nastojato roven 1:4.
Pro nosník čtvercového průřezu (\(\displaystyle a=b\)) roste tuhost se čtvrtou mocninou rozměrů. Obsah (a tedy i hmotnost) roste s druhou mocninou. Uvažujme tři nosníky. První má čtvercový průřez. Druhý také, ale průřez má dvojnásobný obsah. (Strana je tedy \(\displaystyle \sqrt 2\)-krát delší.) Třetí nosník bude krabicový nosník. Bude mít vnější rozměry stejné jako větší nosník, ale uvnitř bude čtvercová dutina o rozměrech prvního nosníku. Tuhost prvního nosníku bude referenční, označme ji \(\displaystyle I\). Tuhost druhého nosníku bude čtyřnásobná, tj. \(\displaystyle 4I\) a za toto navýšení tuhosti „platíme“ použitím dvojnásobného množství materiálu. Tuhost třetího nosníku najdeme jako rozdíl prvních dvou, tj. \(\displaystyle 3I\), protože i geometricky největší nosník vznikne zasunutím prvního nosníku do dutiny ve třetím krabicovém nosníku. Nyní porovnjeme původní nosník a krabicový nosník. Oba používají stejné množství materiálu, ale tuhost krabicového nosníku je trojnásobná. To proto, že část materiálu je dál od osy symetrie průřezu. Podobně se dá zdůvodnit a výpočtem ukázat, že profil ve tvaru písmene I, známé íčko, je tužší než tyč vykovaná ze stejného množství materiálu.
Pro čtvercový průřez roste tuhost se čtvrtou mocninou délky strany. Podobná závislost musí být u každého průřezu jednoparametrického tvaru, například pro kruh. Jako na nosník s kruhovým průřezem můžeme pohlížet i na stromy. Například strom, ve kterém je dutina o velikosti poloviny průměru kmene většinou vyvolá obavy ze stability. I když taková dutina vypadá obrovská, tuhost se sníží o původní tuhost vynásobenou koeficientem
\[(0.5)^4=0.0625\approx 6\%.\]Vidíme, že i s hrozivě vypadající dutinou má kmen pořád tuhost \(\displaystyle 94\%\) původní tuhosti (za předpokladu dutiny uprostřed kmene). Pevnost roste jenom s třetí mocninou a proto odolnost vůči zlomení neklesne tak dramaticky jako tuhost.
6.8.6. Těžiště složeného obrazce#
Uvažujme množinu \(\displaystyle M\) s jednotkovou plošnou hustotou, rozdělenou na dvě disjunktní části \(\displaystyle M_1\) a \(\displaystyle M_2\). Tyto množiny mají \(\displaystyle x\)-ovou polohu těžiště v bodě
Zobecnění výše uvedených myšlenek na množinu rozdělenou na více částí je již snadné.
6.8.7. Steinerova věta#
Nechť je dána množina \(\displaystyle M\) s plošnou hustotou \(\displaystyle \sigma(x,y)\). Ukážeme, že vzhledem k ose procházející těžištěm je nejmenší moment setrvačnosti. Nechť \(\displaystyle m=\iint \sigma(x,y)\,\mathrm dx\mathrm dy\), \(\displaystyle y_0=\frac 1{m}\iint_M y\sigma(x,y)\,\mathrm dx\mathrm dy\) a \(\displaystyle I_{xT}=\iint_M (y-y_0)^2\sigma(x,y)\,\mathrm dx\mathrm dy\) jsou hmotnost, \(\displaystyle y\)-ová poloha těžiště a moment setrvačnosti vzhledem k ose jdoucí těžištěm rovnoběžně s osou \(\displaystyle x\). Moment setrvačnosti vhledem k ose \(\displaystyle x\) je
6.8.8. Tlak na svislou plochu#

Obr. 6.13 Bobři v ZOO v Brně jsou za skleněnou stěnou obdélníkového tvaru.#
Vzorec pro tlakovou sílu \(\displaystyle F=pS\) není možné použít například pro výpočet celkové síly působící na svislou hráz, protože tlak \(\displaystyle p\) se mění s hloubkou a není tedy konstantní na celém průřezu o obsahu \(\displaystyle S\). Ukážeme, jak tuto nesnáz překonat.
Uvažujme svislou rovinnou hráz \(\displaystyle M\). Hrází je přitom myšlena rovinná množina s jednotkovou plošnou hustotou, ne postavený trojrozměrný objekt. Počátek kartézské soustavy souřadnic volíme u hladiny, osa \(\displaystyle y\) směřuje dolů, osa \(\displaystyle x\) vodorovně. Tlak v hloubce \(\displaystyle y\) je roven \(\displaystyle p=y\rho g\), kde \(\displaystyle \rho\) je hustota vody a \(\displaystyle g\) tíhové zrychlení. Na plochu o rozměrech \(\displaystyle \Delta S\) v hloubce \(\displaystyle y\) působí tlaková síla
kde \(\displaystyle p_0=\rho g y_0\) je tlak v těžišti. Proto v praxi stačí znát těžiště hráze a pro výpočet síly na hráz použít celkovou plochu hráze a tlak v těžišti. Protože jsme pracovali s obecnou množinou \(\displaystyle M\), není tento poznatek nijak vázán na konkrétní tvar hráze. Musí být však splněna podmínka, že všechny body hráze leží v jedné rovině.
Ve výpočtu výše jsme uvažovali svislou rovinu, ale zobecnění na šikmou rovinu je snadné. Stačí opravit vztah pro hloubku, protože když svislou množinu i s kartézskými souřadnicemi pootočíme okolo osy procházející hladinou, hloubka všech bodů se sníží faktorem \(\displaystyle \sin \alpha\), kde \(\displaystyle \alpha\) je úhel mezi vodorovnou hladinou a rovinou hráze. Formálně tato operace dopadne stejně, jako kdybychom tekutinu nahradili tekutinou s hustotou \(\displaystyle \sin\alpha\)-krát nižší. Protože však vztah (6.1) nezávisí na hustotě, nic se na něm nezmění. Také zobecnění na několik rovin je snadné. Zobecnění na zakřivenou plochu je náročnější a vyžaduje jiný typ integrálu.
V předchozím textu jsme proměnnou veličinu popisující tlak na hráz jako funkci hloubky nahradili konstantní veličinou, udávající tlak v těžišti. Výsledný účinek na hráz se nezměnil. To je přesně smysl střední hodnoty. V matematických pojmech je možno říci, že střední hodnota tlaku na svislou hráz je rovna tlaku v těžišti hráze. (Protože hrází myslíme spíše rovinnou plochu, tak by přesnější terminologie měla používat raději pojem geometrický střed. Budeme se však držet ustálené terminologie.)
Nikde ve výpočtu jsme nepoužili konkrétní meze pro integraci. Výsledek tedy platí nejenom pro hráz dosahující k hladině, ale například i pro poklop výpusti, který je celý pod vodou.
6.8.9. Působiště tlakové síly#
Budeme pokračovat v předchozím příkladě a hledat působiště výsledné tlakové síly.
Tlaková síla působící na svislou hráz má celkový nulový moment vzhledem k ose procházející působištěm. Je-li hráz definována množinou \(\displaystyle M\) a je-li \(\displaystyle y_c\) působiště výsledné tlakové síly, je v hloubce \(\displaystyle y\) tlak na plošku o velikosti \(\displaystyle \Delta S\) roven \(\displaystyle y\rho g \Delta S\) a součin \(\displaystyle (y_c-y)y\rho g\Delta S\) je příspěvek k otáčivému momentu vzhledem k ose, procházející vodorovně působištěm tlakové síly. Součet všech těchto příspěvků se nuluje, tedy musí platit
Formálně vztah pro \(\displaystyle y_c\) odpovídá vztahu pro těžiště množiny s plošnou hustotou \(\displaystyle y\). Na tomto pozorování a na skutečnosti, že u pravidelných množin umíme těžiště najít geometricky, je založena metoda nalezení působiště tlakové síly pomocí zatěžovacího obrazce.
Kvadratický moment v čitateli zlomku \(\displaystyle \eqref{H2}\) vyjadřujícího \(\displaystyle y_c\) je často výhodnější rozepsat pomocí Steinerovy věty. Ve jmenovateli je součin obsahu \(\displaystyle S\) a \(\displaystyle y\)-ové souřadnice těžiště \(\displaystyle y_0\). Tím dostaneme
6.9. Dvojný integrál v polárních souřadnicích#
6.9.1. Polární souřadnice#
Dosud jsme používali pouze kartézské souřadnice: dvojici čísel udávající vzdálenost bodu od osy \(\displaystyle y\) a od osy \(\displaystyle x\), která jednoznačně určuje polohu bodu v rovině. V praxi je někdy výhodnější použít i jiný způsob jak pomocí dvojice čísel charakterizovat polohu bodu v rovině - takové souřadnice potom nazýváme křivočaré souřadnice.
Z křivočarých souřadnic jsou nejdůležitější polární souřadnice. Při jejich použití polohu bodu \(\displaystyle A\) zadáváme tak, že určíme vzdálenost \(\displaystyle r\) bodu od počátku soustavy souřadnic \(\displaystyle O\) a úhel \(\displaystyle \varphi\), který svírá spojnice bodů \(\displaystyle O\) a \(\displaystyle A\) s kladnou částí osy \(\displaystyle x\).
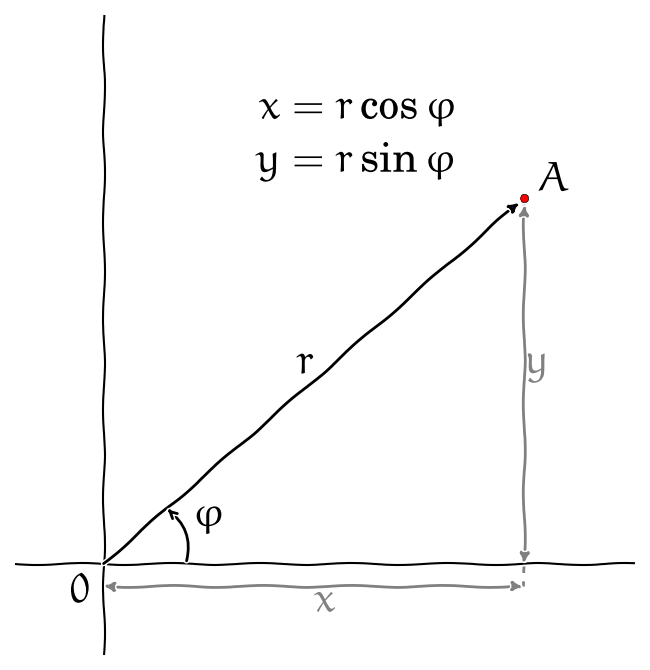
Obr. 6.14 Polární souřadnice.#
6.9.2. Množiny s jednoduchým vyjádřením v polárních souřadnicích#
Nejsnáze se při výpočtu dvojného integrálu pracuje s obdélníkovými množinami, tj. s množinami charakterizovanými nerovnostmi pro jednotlivé proměnné a konstantním omezením pro tyto proměnné. Analogicky se bude snadno pracovat v polárních souřadnicích s množinami, které by se staly obdélníky pro překreslení do souřadné soustavy \(\displaystyle r\) a \(\displaystyle \varphi\). Takové množiny jsou zobrazeny na následujících obrázcích.
Obrázek |
Popis v polárních souřadnicích |
Popis v kartézských souřadnicích |
|---|---|---|
|
\[\begin{split}\begin{gathered}0\leq r\leq 1 \\ 0\leq \varphi\leq 2\pi\end{gathered}\end{split}\]
|
\[\begin{split}\begin{gathered}-1\leq x\leq 1\\ -\sqrt{1-x^2}\leq y\leq \sqrt{1-x^2}\end{gathered}\end{split}\]
|
|
\[\begin{split}\begin{gathered}1\leq r\leq 2 \\ 0\leq \varphi\leq \frac \pi2\end{gathered}\end{split}\]
|
Nelze zapsat pomocí jedné dvojice nerovností |
|
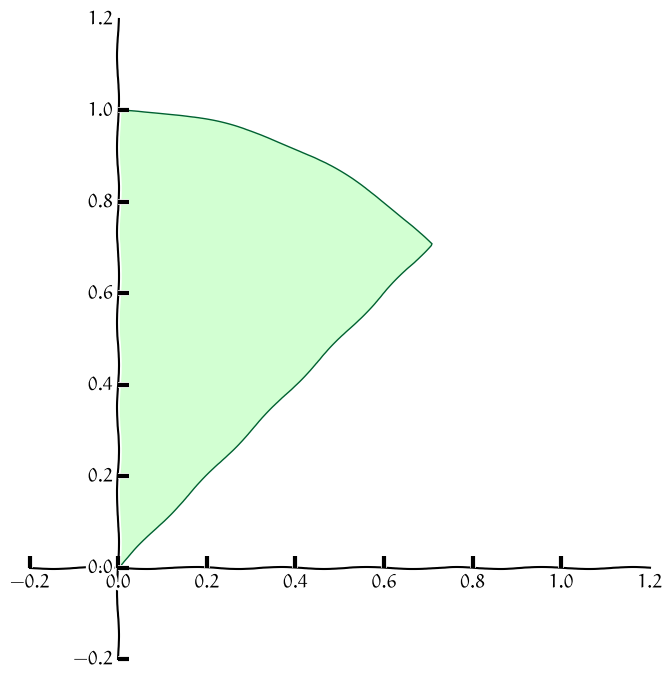
\[\begin{split}\begin{gathered}0\leq r\leq 1 \\ \frac\pi 4\leq \varphi\leq \frac\pi 2\end{gathered}\end{split}\]
|
\[\begin{split}\begin{gathered}0\leq x\leq \frac {\sqrt 2}2 \\ x\leq y\leq \sqrt{1-x^2}\end{gathered}\end{split}\]
|
6.9.3. Převod dvojného integrálu do polárních souřadnic#
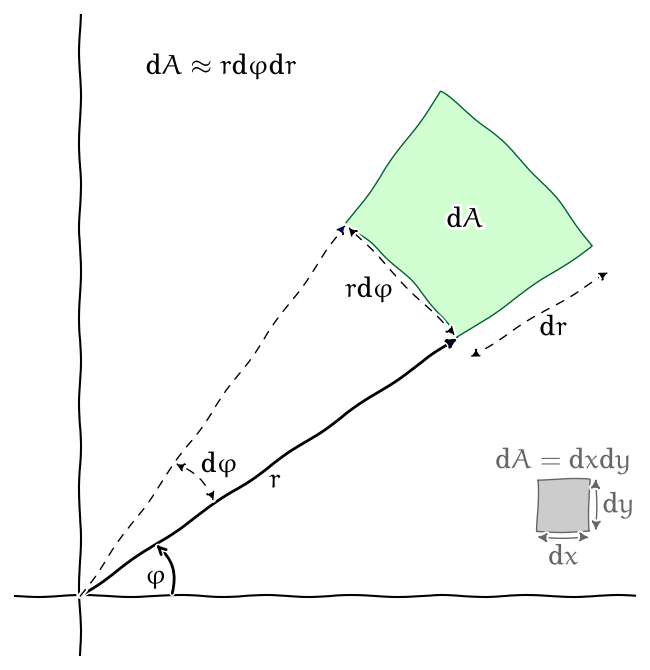
Obr. 6.15 Element plochy v polárních souřadnicích#
Chceme-li převést dvojný integrál do polárních souřadnic, provádíme v něm vlastně substituci \(\displaystyle x=r\cos \varphi\) a \(\displaystyle y=r\sin \varphi\). Přitom se transformují i diferenciály \(\displaystyle \mathrm{d}x\) a \(\displaystyle \mathrm{d}y\). Při změně úhlu o \(\displaystyle \mathrm{d}\varphi\) a změně vzdálenosti o \(\displaystyle \mathrm{d}r\) má odpovídající část roviny rozměry \(\displaystyle \mathrm{d}r\) a \(\displaystyle r\mathrm{d}\varphi\) a její obsah je \(\displaystyle r\mathrm{d}\varphi\mathrm{d}r\) (viz obrázek). Platí tedy, že obsah elementární oblasti \(\displaystyle \mathrm{d} A=\mathrm{d} x\mathrm{d}y\) se transformuje na \(\displaystyle \mathrm{d} A=r\mathrm{d}\varphi\mathrm{d}r\). Podíl \(\displaystyle \frac{\mathrm{d}\varphi\mathrm{d}r }{\mathrm{d}x \mathrm{d}y }\) udává, kolikrát se změní obsah elementární oblasti při změně souřadnic a nazývá se jakobián. V případě polárních souřadnic je jakobián jak vidíme roven \(\displaystyle r\) a platí tedy
V diferenciálním počtu polární souřadnice používáme především tam, kde má problém radiální symetrii. Například při studiu ochlazování nebo kmitů kruhových desek či válcovitých součástek. V integrálním počtu tyto souřadnice použijeme zejména v případě, kdy integrujeme přes kružnici nebo její část (např. mezikruží či kruhová výseč). V takovém případě mají totiž integrály které vzniknou po transformaci dvojného integrálu na dvojnásobný pevné meze a výpočet druhého integrálu je zpravidla jednodušší.
6.10. Z ptačí perspektivy#

Obr. 6.16 Ještě pohled s trochou nadhledu. Zdroj: pixabay.com#
Dvojný integrál využijeme tam, kde nás zajímá celková hodnota aditivní veličiny, jejíž příspěvky jsou rozloženy ve dvourozměrné ploše. Například celková tlaková síla na stěnu akvária.
Dvojný integrál počítáme jako integrál z integrálu aparátem integrálního počtu funkcí jedné proměnné. V řadě případů se však problém dá zjednodušit. Například při integrování funkcí se separovanými proměnnými přes obdélníkové množiny se integrál dá zapsat jako součin integrálů. Podobně, při integrování přes množiny které jsou částmi kruhu se dá v mnoha případech integrál přepsat pomocí polárních souřadnic na integrál přes obdélník (v polárních souřadnicích).