5. Křivkové integrály

Anotace.

• V úvodu si ukážeme vektorové pole, kde výpočet po třech různých křivkách mezi stejnými body, vede ke třem různým výsledkům.

• Poté zkusíme vypočítat bez bližšího kontextu několik křivkových integrálů pro pro získání určité míry jistoty při práci s tímto integrálem.

• Poté se zaměříme tok vektorového pole křivkou a ukážeme si souvislost výsledného toku s grafickým znázorněním situace.

• Odhadu křivkového integrálu a toku křivkou se budeme věnovat v posledním příkladě. Naučíme se, čeho si všímat, když chceme zjistit, zda je výsledný integrál nebo tok kladný nebo záporný.

5.1. Křivkový integrál druhého druhu po třech různých křivkách

Video

Vypočtěte

\[\int_{C_i} \vec F \mathrm d\vec r\]

pro vektorové pole

\[\vec F=-y\vec \imath + x\vec\jmath\]

po třech různých křivkách \(\displaystyle C_1\), \(\displaystyle C_2\) a \(\displaystyle C_3\).

\[\begin{split}\begin{aligned} C_1&\colon \vec r=\cos(t)\vec \imath + \sin (t)\vec\jmath, \quad t\in\qty[0,\frac\pi 2]\\ C_2&\colon \vec r=(1-t)\vec \imath + t\vec\jmath, \quad t\in\qty[0,1]\\ C_3&\colon \vec r=(1-t^2)\vec \imath + t\vec\jmath, \quad t\in\qty[0,1] \end{aligned}\end{split}\]

Tj. počítáme

\[\int_{C_i} -y\,\mathrm dx + x\,\mathrm dy\]

po třech zadaných křivkách \(\displaystyle C_1\), \(\displaystyle C_2\) a \(\displaystyle C_3\).

Řešení

Vektory budeme pro stručnost zapisovat jako uspořádané dvojice.

Křivka \(\displaystyle C_1\). Derivací křivky \(\displaystyle \vec r=(\cos(t),\sin(t))\) podle \(\displaystyle t\) dostáváme

\[\frac{\mathrm d\vec r}{\mathrm dt}=(-\sin (t),\cos (t)).\]

Rovnice vektorového pole podél křivky má tvar

\[\vec F(\vec r(t))=(-\sin t,\cos t).\]

Skalárním součinem dostáváme

\[\vec F \frac{\mathrm d\vec r}{\mathrm dt}=(-\sin t,\cos t)\cdot (-\sin (t),\cos (t)) = \sin^2 t+\cos^2 t =1. \]

Odsud formálně

\[\vec F\mathrm d\vec r=1\mathrm dt\]

a integrál má tvar

\[\int_C\vec F\mathrm d\vec r=\int_0^{\frac \pi 2}1\,\mathrm dt=\frac \pi 2,\]

kde poslední Riemannův integrál není nutné počítat, protože integrál z jedničky je délka intervalu, přes který se integruje.

Křivka \(\displaystyle C_2\). Derivací křivky \(\displaystyle \vec r=(1-t,t)\) podle \(\displaystyle t\) dostáváme

\[\frac{\mathrm d\vec r}{\mathrm dt}=(-1,1).\]

Rovnice vektorového pole podél křivky má tvar

\[\vec F(\vec r(t))=(-t,1-t).\]

Skalárním součinem dostáváme

\[\vec F \frac{\mathrm d\vec r}{\mathrm dt}=(-t,1- t)\cdot (-1,1) = (-t)(-1)+(1-t)\cdot 1 =1. \]

Odsud formálně

\[\vec F\mathrm d\vec r=1\mathrm dt\]

a integrál má tvar

\[\int_C\vec F\mathrm d\vec r=\int_0^{1}1\,\mathrm dt=1,\]

kde ani v tomto případě poslední Riemannův integrál není nutné počítat, protože integrál z jedničky je délka intervalu, přes který se integruje.

Křivka \(\displaystyle C_3\). Derivací křivky \(\displaystyle \vec r=(1-t^2,t)\) podle \(\displaystyle t\) dostáváme

\[\frac{\mathrm d\vec r}{\mathrm dt}=(-2t,1).\]

Rovnice vektorového pole podél křivky má tvar

\[\vec F(\vec r(t))=(-t,1-t^2).\]

Skalárním součinem dostáváme

\[\vec F \frac{\mathrm d\vec r}{\mathrm dt}=(-t,1- t^2)\cdot (-2t,1) = (-t)(-2t)+(1-t^2)\cdot 1 =t^2+1. \]

Odsud formálně

\[\vec F\mathrm d\vec r=(t^2+1)\mathrm dt\]

a integrál má tvar

\[\int_C\vec F\mathrm d\vec r=\int_0^{1}(t^2+1)\,\mathrm dt=\qty[\frac 13 t^3 + t]_0^1 = \frac 13 + 1 - 0 =\frac 43. \]

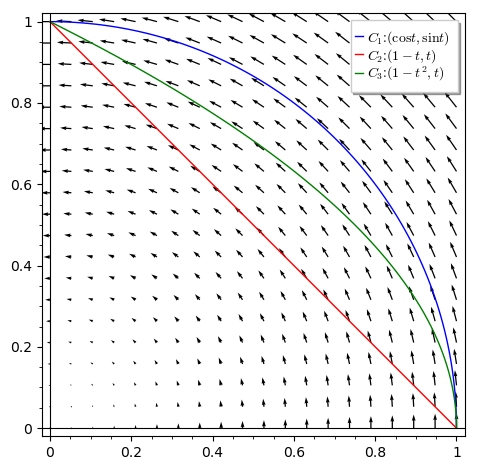
Obr. 5.12 Zdroj: vlastní

Interpretace jako práce, srovnání.

Všechny křivky jsou z bodu \(\displaystyle [1,0]\) do bodu \(\displaystyle [0,1]\). Nejblíže k počátku je úsečka \(\displaystyle C_2\), nejdále je čvrtkružnice \(\displaystyle C_1\), křivka \(\displaystyle C_2\) je mezi nimi.

Integrál fyzikálně znamená práci vektorového pole \(\displaystyle (-y,x)\) po zadané křivce. Toto vektorové pole míří po kružnicích okolo počátku proti směru hodinových ručiček. Délka vektoru je rovna vzdálenosti od počátku.

Křivka \(\displaystyle C_1\) je nejdále od počátku a vektorové pole je na ní nejsilnější. Navíc v každém bodě je síla ve směru křivky a proto se projeví ve výsledném příspěvku bez redukování. Díky tomu můžeme integrál po kružnici počítat stejně jako práci na přímce, tj. součinem délky křivky \(\displaystyle \frac \pi 2\) a velikosti síly \(\displaystyle |\vec F|=1\). Po dalších křivkách je síla menší (křivky jdou blíže ke středu) a navíc se neuplatní celá velikost síly, protože síla svírá s křivkou nenulový úhel a při práci se projeví pouze tečná komponenta.

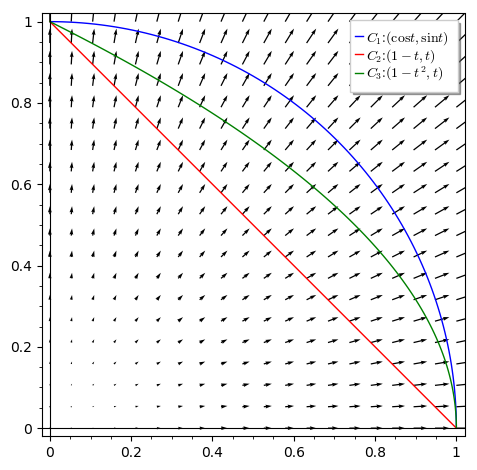
Obr. 5.13 Zdroj: vlastní

Interpretace jako tok, srovnání.

Všechny křivky jsou z bodu \(\displaystyle [1,0]\) do bodu \(\displaystyle [0,1]\). Nejblíže k počátku je úsečka \(\displaystyle C_2\), nejdále je čvrtkružnice \(\displaystyle C_1\), část paraboly \(\displaystyle C_2\) je mezi nimi.

Integrál fyzikálně znamená tok vektorového pole \(\displaystyle (x,y)\) křivkou. Toto vektorové pole míří směrem z počátku a zesiluje směrem od počátku, protože délka vektoru je rovna vzdálenosti od počátku.

Proto je hodnota po křivce nejblíže počátku nejmenší atd. Na křivce \(\displaystyle C_1\) (kružnice) je tok v každém bodě kolmý ke křivce a stejně velký a proto je celkový tok snadné určit jako součin velikosti vektorového pole na křivce (\(\displaystyle |\vec F|=1\)) a délky křivky \(\displaystyle \frac \pi 2\).

5.2. Křivkový integrál druhého druhu po parabole

Video

Vypočtěte

\[\int_{C} \vec F \mathrm d\vec r\]

pro vektorové pole

\[\vec F=x^2\vec \imath + (x+y)\vec\jmath\]

po části paraboly

\[\begin{aligned} C&\colon \vec r=t\vec \imath + t^2\vec\jmath, \quad t\in\qty[0,1] \end{aligned}\]

tj. počítáme

\[\int_C x^2\,\mathrm dx + (x+y)\,\mathrm dy\]

po zadané křivce \(\displaystyle C\).

Řešení

Vektory budeme pro stručnost zapisovat jako uspořádané dvojice.

Derivací křivky \(\displaystyle \vec r=(t,t^2)\) podle \(\displaystyle t\) dostáváme

\[\frac{\mathrm d\vec r}{\mathrm dt}=(1,2t).\]

Rovnice vektorového pole podél křivky má tvar

\[\vec F(\vec r(t))=(t^2,t+t^2).\]

Skalárním součinem dostáváme

\[\vec F \frac{\mathrm d\vec r}{\mathrm dt}=(1,2t)\cdot (t^2,t+t^2) = 1\cdot t^2+2t\cdot(t+t^2)=3t^2+2t^3. \]

Odsud formálně

\[\vec F\mathrm d\vec r=(3t^2+2t^3)\mathrm dt\]

a integrál má tvar

\[\int_C\vec F\mathrm d\vec r=\int_0^{1}(3t^2+2t^3)\,\mathrm dt=\qty[t^3+\frac 12 t^4]_0^1=1+\frac 12 - 0 = \frac 32.\]

5.3. Křivkový integrál druhého druhu po kubické parabole

Vypočtěte

\[\int_{C} \vec F \mathrm d\vec r\]

pro vektorové pole

\[\vec F=2y\vec \imath + x^2y\vec\jmath\]

po části kubické paraboly

\[\begin{aligned} C&\colon \vec r=t\vec \imath + t^3\vec\jmath, \quad t\in\qty[0,1], \end{aligned}\]

tj. počítáme

\[\int_C 2y\,\mathrm dx + x^2y\,\mathrm dy\]

po zadané křivce \(\displaystyle C\).

Řešení

Vektory budeme pro stručnost zapisovat jako uspořádané dvojice.

Derivací křivky \(\displaystyle \vec r=(t,t^3)\) podle \(\displaystyle t\) dostáváme

\[\frac{\mathrm d\vec r}{\mathrm dt}=(1,3t^2).\]

Rovnice vektorového pole podél křivky má tvar

\[\vec F(\vec r(t))=(2t^3,t^2t^3)=(2t^3,t^5).\]

Skalárním součinem dostáváme

\[\vec F \frac{\mathrm d\vec r}{\mathrm dt}=(1,3t^2)\cdot (2t^3,t^5) = 1\cdot 2t^3+3t^2\cdot t^5=2t^3+3t^7. \]

Odsud formálně

\[\vec F\mathrm d\vec r=(2t^3+3t^7)\mathrm dt\]

a integrál má tvar

\[\int_C\vec F\mathrm d\vec r=\int_0^{1}(2t^3+3t^7)\,\mathrm dt=\qty[\frac 12 t^4 + \frac 38 t^8]_0^1=\frac 12 +\frac 38 - 0 = \frac 78.\]

Testová otázka Testová otázka

5.4. Tok vektorového pole uzavřenou křivkou

Video

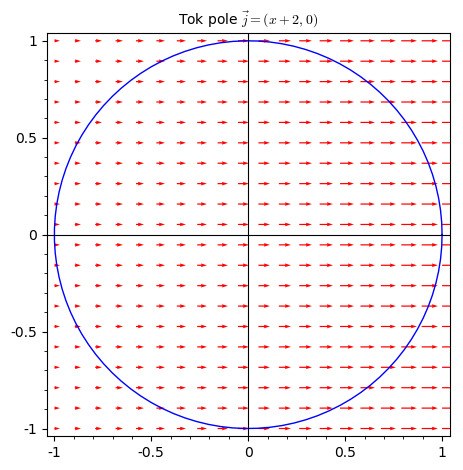
Obr. 5.14 Zdroj: vlastní

Vypočtěte tok vektorového pole

\[\vec \Phi_1=(x+2)\vec\imath\]

jednotkovou kružnicí se středem v počátku orientovanou proti směru hodinových ručiček, tj.

\[C\colon \vec r=\cos(t)\vec \imath+\sin(t)\vec\jmath, \quad t\in[0,2\pi].\]

Návod: Platí

\[\int_0^{2\pi}\sin^2 t\,\mathrm dt=\int_0^{2\pi}\cos^2 t\,\mathrm dt= \pi\]

a tento integrál je možno najít například grafickou cestou.

Řešení

Vektorové pole teče směrem doprava a směrem doprava i zesiluje. Dá se čekat, že tok ven pravou polovinou kružnice bude větší než tok dovnitř levou polovinou kružnice a celkový tok bude nenulový.

Vektorové pole je

\[\vec \Phi_1=(x+2,0)\]

a pro výpočet toku musíme integrovat křivkovým integrálem druhého druhu vektorové pole

\[\vec F=(0,x+2).\]

Vskutku, tok vektorového pole zadaného v komponentách \(\displaystyle \Phi_1=(P,Q)\) je vyjádřen integrálem druhého druhu vektorového pole \(\displaystyle \vec F=(-Q,P)\) a v našem případě je \(\displaystyle P=x+2\) a \(\displaystyle Q=0\). Derivací rovnice křivky obdržíme

\[\frac{\mathrm d\vec r}{\mathrm dt}=(-\sin (t),\cos (t)).\]

Rovnice vektorového pole \(\displaystyle \vec F\) podél křivky \(\displaystyle C\) má tvar

\[\vec F(\vec r(t))=(0,2+\cos t).\]

Skalárním součinem dostáváme

\[\vec F \frac{\mathrm d\vec r}{\mathrm dt}=(-\sin t,\cos t)\cdot (0,2+\cos (t)) = 2\cos t+\cos^2 t . \]

Odsud formálně

\[\vec F\mathrm d\vec r=(2\cos t+\cos^2 t)\mathrm dt\]

a integrál má tvar

\[\oint_C\vec F\mathrm d\vec r=\int_0^{2\pi }(2\cos t+\cos^2 t)\,\mathrm dt= \pi ,\]

kde poslední Riemannův integrál není nutné počítat, protože integrál z první části je nulový díky geometrické interpretaci integrálu a periodicitě funkce \(\displaystyle \cos t\) a integrál z druhého sčítance byl součástí zadání.

5.5. Tok vektorového pole uzavřenou křivkou II

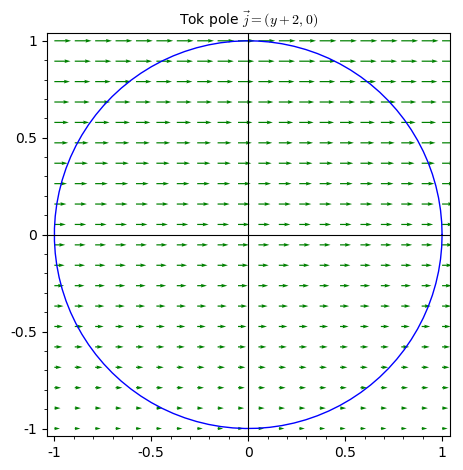
Obr. 5.15 Zdroj: vlastní

Vypočtěte tok vektorového pole

\[\vec \Phi_2=(y+2)\vec\imath\]

jednotkovou kružnicí se středem v počátku orientovanou proti směru hodinových ručiček, tj.

\[C\colon \vec r=\cos(t)\vec \imath+\sin(t)\vec\jmath, \quad t\in[0,2\pi].\]

Návod: Platí

\[\int_0^{2\pi}\sin t\cos t\,\mathrm dt=0.\]

Řešení

Vektorové pole teče směrem doprava. Kromě toho zesiluje směrem nahoru. Dá se čekat, že tok ven pravou polovinou kružnice bude v každé výšce stejný jako tok dovnitř levou polovinou kružnice a celkový tok bude nulový.

Vektorové pole je

\[\vec \Phi_2=(y+2,0)\]

a pro výpočet toku musíme integrovat křivkovým integrálem druhého druhu vektorové pole

\[\vec F=(0,y+2).\]

Vskutku, tok vektorového pole zadaného v komponentách \(\displaystyle \Phi_2=(P,Q)\) je vyjádřen integrálem druhého druhu vektorového pole \(\displaystyle \vec F=(-Q,P)\) a v našem případě je \(\displaystyle P=y+2\) a \(\displaystyle Q=0\). Derivací rovnice křivky obdržíme

\[\frac{\mathrm d\vec r}{\mathrm dt}=(-\sin (t),\cos (t)).\]

Rovnice vektorového pole \(\displaystyle \vec F\) podél křivky \(\displaystyle C\) má tvar

\[\vec F(\vec r(t))=(0,2+\sin t).\]

Skalárním součinem dostáváme

\[\vec F \frac{\mathrm d\vec r}{\mathrm dt}=(-\sin t,\cos t)\cdot (0,2+\sin (t)) = 2\cos t+\cos t \sin t. \]

Odsud formálně

\[\vec F\mathrm d\vec r=(2\cos t+\cos t\sin t)\mathrm dt\]

a integrál má tvar

\[\oint_C\vec F\mathrm d\vec r=\int_0^{2\pi }(2\cos t+\cos t\sin t)\,\mathrm dt.\]

Integrál z prvního sčítance můžeme vypočítat pomocí primitivní funkce

\[\int_0^{2\pi} 2\cos x\,\mathrm dx=\qty[2\sin x]_0^{2\pi}=2\sin(2\pi)-2\sin 0 =0\]

a integrál z druhého sčítance je nulový, proto je nulový i celý integrál.

\[\int_C\vec F\mathrm d\vec r=0\]

5.6. Křivkový integrál a tok graficky

Video

Vyřešte příklady na následujících odkazech. Řiďte se popsaným pravidlem, nebo pravidlem uvedeným ve videokomentáři.

5.6.1. Křivkový integrál

• Pokud křivka a vektorové pole svírají ostrý úhel, je příspěvek k celkové hodnotě integrálu kladný. Pokud jsou přesně stejným směrem (nulový úhel) je příspěvek roven součinu.

• Pokud křivka a vektorové pole svírají tupý úhel, je příspěvek k celkové hodnotě integrálu záporný. Pokud jsou přesně opačným směrem (úhel \(\displaystyle 180^\circ\)) je příspěvek roven záporně vzatém součinu.

• Intenzivnější vektorové pole nebo delší křivka produkují větší numerickou hodnotu integrálu (více kladnou nebo více zápornou, podle znaménka). Pole více kolmo na křivku produkuje menší numerickou hodnotu integrálu (blíže k nule).

Testová otázka Testová otázka Testová otázka Testová otázka

5.6.2. Tok

• Pravidla pro souvislost toku s intenzitou pole a délkou křivky jsou analogická jako u křivkového integrálu (delší křivka a intenzivnější vektorové pole způsobují větší tok).

• Pokud se díváme ve směru křivky a pole přestupuje přes křivku zleva doprava, je tok kladný, v opačném případě záporný.

Testová otázka