4. Rotace vektorového pole#
Anotace.
Již nějakou dobu studujeme vektorová pole. V této přednášce si několik typických zkusíme vizualizovat.
Seznámíme se s pojmy kmenová funkce, skalární potenciál, kmenová funkce. Tyto pojmy udávají, zda vektorové pole je či není možné obdržet jako výsledek výpočtu gradientu nějaké skalární funkce. Není to akademická otázka, ale odpověď má dalekosáhlé důsledky. Zjednodušeně řečeno, pokud je odpověď kladná, dají se některé úlohy místo ve vektorovém poli řešit v poli skalárním, což nese výrazné usnadnění.
S výše uvedenou problematikou souvisí pojem rotace vektorového pole, který si uvedeme jako další z diferenciálních operátorů vektorové analýzy.
Ukážeme si, že parciální derivace jsou vhodným nástrojem pro jakousi citlivostní analýzu. Seznámíme se v této souvislosti se zákonem šíření chyb.
Prerekvizity.
I zde budeme pracovat s diferenciálními operátory. Je žádoucí umět spolehlivě derivovat.
Budeme počítat vektorový součin vektorů. Ten je nejsnazší počítat pomocí determinantů třetího řádu. Tuto dovednost tedy využijeme.
4.1. Vektorová pole#
Studujeme funkce \(\displaystyle \mathbb{R}^2\to\mathbb{R}^2\) nebo \(\displaystyle \mathbb{R}^3\to\mathbb{R}^3\).
Uspořádané dvojice nebo trojice na vstupu vektorového pole chápeme jako body v rovině nebo v prostoru. Uspořádané dvojice nebo trojice na výstupu chápeme jako vektory. Bodům v rovině nebo v prostoru jsou tedy přiřazeny vektory. Můžeme proto vektorové pole interpretovat jako rychlostní pole nebo silové pole.
2D: \(\displaystyle \vec F:\mathbb {R}^2 \to \mathbb {R}^2\). Ve složkách píšeme
\[ \vec F = (P, Q) = P\vec \imath + Q\vec \jmath,\]kde \(\displaystyle P\) a \(\displaystyle Q\) jsou (skalární) funkce dvou proměnných.3D: \(\displaystyle \vec F:\mathbb {R}^3 \to \mathbb {R}^3\). Ve složkách píšeme
\[ \vec F = (P, Q, R) = P\vec \imath + Q\vec \jmath + R\vec k,\]kde \(\displaystyle P\), \(\displaystyle Q\) a \(\displaystyle R\) jsou (skalární) funkce tří proměnných.
4.2. Příklady vektorových polí v rovině#
Předpis
\[\vec F_1=(0,-1)=-\vec \jmath\]definuje homogenní pole. Každý vektor je stejný (směr i velikost).Předpis
\[\vec F_2=(x,y)=x\vec \imath+y\vec \jmath\]definuje radiální pole. Každý vektor směřuje od počátku souřadnic.Předpis
\[\vec F_3=(-y,x)=-y\vec \imath+x\vec \jmath\]definuje rotující pole. Je kolmé na radiální pole. Každý vektor je tečný ke kružnici se středem v počátku souřadnic. Nakreslit online.Předpis
\[\vec F_4=\frac{\vec F_2}{|\vec F_2|}=\frac{(x,y)}{\sqrt{x^2+y^2}}=\frac{x\vec \imath +y\vec \jmath}{\sqrt{x^2+y^2}}\]definuje radiální pole s konstantní velikostí vektorů. Každý vektor směřuje od počátku souřadnic a má jednotkovou délku.Předpis
\[\vec F_5=-\frac{\vec F_4}{x^2+y^2}=-\frac{x \vec \imath+y\vec \jmath}{(x^2+y^2)^{3/2}}\]definuje radiální pole ubývající s kvadrátem vzdálenosti od počátku a mířící do středu. S druhou mocninou ve jmenovateli ubývá například 3D gravitační pole nebo elektrostatické pole generované hmotným bodem nebo koulí.Rychlost při proudění vazké tekutiny ubývá směrem ke stěnám. Tekutinu proudící doprava je možné pro \(\displaystyle y\in [0,1]\) modelovat vektorovým polem
\[\vec F_6=(y(1-y),0)=y(1-y)\vec \imath.\]
4.3. Totální diferenciál#
Definice (totální diferenciál)
Totálním diferenciálem funkce \(\displaystyle z=f(x,y)\) v bodě \(\displaystyle (x_0, y_0)\) nazýváme výraz
V souvislosti s totálním diferenciálem často vyvstává otázka, zda pro zadané vektorové pole
Věta (nutná a postačující podmínka pro existenci kmenové funkce ve 2D)
Vektor
Jeden směr implikace v předchozí větě je snadný a plyne hned ze Schwarzovy věty.
4.4. Skalární a vektorový součin#
Diferenciální operátor divergence jsme poznali v minulé přednášce v souvislosti s difuzní rovnicí. Formálně jde o skalární součin operátoru \(\displaystyle \nabla\) definovaného vztahem
Vektorovým součinem \(\displaystyle \vec a \times \vec b\) vektorů \(\displaystyle \vec a=(a_1,a_2,a_3)\) a \(\displaystyle \vec b=(b_1,b_2,b_3)\) rozumíme vektor
4.5. Rotace#
Definice (rotace vektorového pole)
Pro vektorovou funkci tří proměnných
Výsledkem rotace je tedy vektorové pole, jehož komponenty jsou
\[\nabla \times \vec F=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\vec \imath +\left( \frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\vec \jmath + \left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\vec k.\]
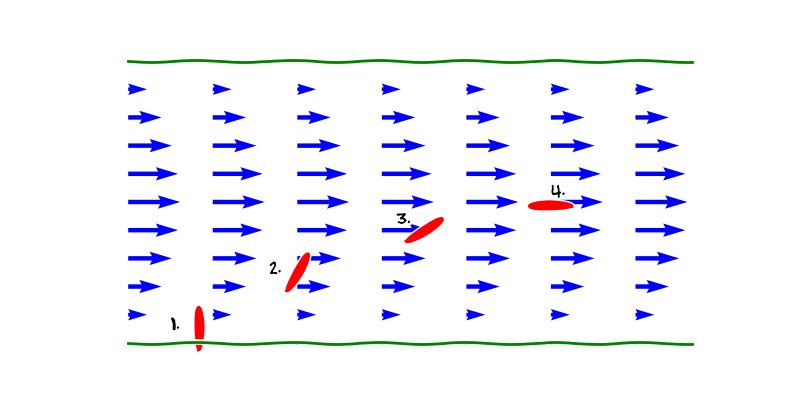
Obr. 4.1 Tok kapaliny mezi dvěma rovnoběžnými stěnami jako pole s nenulovou rotací. Rychlost proudu klesá kvadraticky směrem ke břehům a díky tomu se loďka, která odrazí od břehu kolmo, stáčí po proudu.#

Ve dvourozměrném vektorovém poli doplníme třetí komponentu nulovou. Rotace má potom první dvě komponenty nulové (\(\displaystyle R=\frac{\partial Q}{\partial z}=\frac{\partial P}{\partial z}=0\)). Třetí komponenta rotace dvourozměrného vektorového pole je nulová právě tehdy, když k tomuto vektorovému poli existuje skalární potenciál.
Ve fyzice má důležité postavení vektorové pole s nulovou rotací. Je v něm totiž možno zavést potenciál a potenciální energii. Takové pole se nazývá nevírové pole.
Představme si vektorové pole charakterizující rychlost proudící tekutiny. Rotace udává, zda má pole tendenci uvést do rotace objekt unášený tímto prouděním. Jedná se o lokální charakteristiku a nesouvisí se směrem proudění. Rotace může být nulová i pro tok cirkulující okolo jednoho bodu (uvidíme níže). Naopak, pro to v přímce může být rotace nenulová. Příkladem je přímý tok v řece, kdy rychlost u břehu klesá. V důsledku toho se loďka, která odrazí od břehu kolmo stočí po proudu. Mimo středovou osu má pole nenulovou rotaci, i když ve všech bodech míří stejným směrem. Online výpočet.
Pozor: anglický výraz pro rotaci je „curl“.
Poznámka (linearita rotace)
Rotace zachovává součet a násobení konstantou, tj. pro libovolné vektorové funkce \(\displaystyle \vec F\) a \(\displaystyle \vec G\) a konstantu \(\displaystyle c\) platí
4.6. Rotace významných polí#
Dostředivé pole ubývající s libovolnou mocninou vzdálenosti má nulovou rotaci. Pro
\[\vec F(x,y)=-\frac{x\vec \imath +y \vec \jmath}{(x^2+y^2)^n}\]platí\[\nabla\times \vec F(x,y)=0.\]Online výpočet.Rotace pole kolmého na dostředivé pole závisí na mocnině, se kterou toto pole ubývá. Pro
\[\vec F(x,y)=\frac{-y\vec \imath +x\vec \jmath}{(x^2+y^2)^n}\]platí\[\nabla\times \vec F(x,y)=-\frac{2(n-1)}{(x^2+y^2)^n}\vec k.\]Pro různé \(\displaystyle n\) toto pole cirkuluje okolo počátku proti směru hodinových ručiček. Rotace (ve smyslu operátoru rotace) však může být kladná i záporná, což je určeno znaménkem výrazu \(\displaystyle n-1\). Pokud bychom takovým polem nechali unášet drobný míček, v jednom případě by jej pole otáčelo po směru a v jiném případě proti směru hodinových ručiček. Pro \(\displaystyle n=1\) by se míček neroztočil okolo vlastní osy vůbec, rotace je nulová. Online výpočet. Nakreslit online.
4.7. Zákon šíření chyb (chyba nepřímo měřené veličiny)#
Některé veličiny neměříme přímo, ale vypočítáváme z jiných naměřených veličin. Takové veličiny se nazývají nepřímo měřené veličiny.
Předpokládejme, že měříme nepřímo veličinu \(\displaystyle f\) tak, že měříme veličiny \(\displaystyle x_1\), \(\displaystyle x_2\), \(\displaystyle \dots\), \(\displaystyle x_n\) a hodnotu veličiny \(\displaystyle f\) určíme pomocí vzorce \(\displaystyle f(x_1, x_2, \dots, x_n)\).
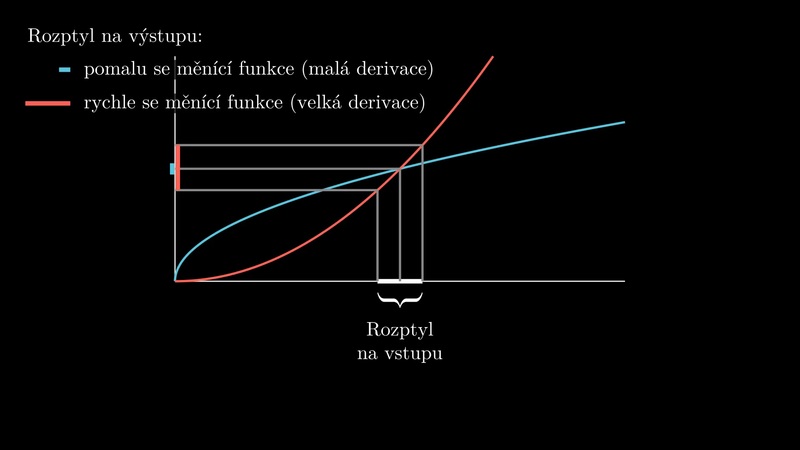
Měření každé z veličin je zatíženo chybou. Je-li chyba veličiny \(\displaystyle x_i\) rovna \(\displaystyle \Delta x_i\), způsobí tato odchylka to, že chyba veličiny \(\displaystyle f\) bude (v souladu se vzorcem pro lineární aproximaci) přibližně
\[ \Delta f\approx \left|\frac{\partial f}{\partial x_i}\Delta x_i\right| \]Celkovou chybu veličiny \(\displaystyle f\) můžeme určit sečtením chyb způsobených jednotlivými veličinami \(\displaystyle x_i\). Častěji se však používá následující vzorec
\[ \Delta f(x_1,x_2,\dots x_n)\approx\sqrt{\left(\frac{\partial f}{\partial x_1}\Delta x_1\right)^2+\left(\frac{\partial f}{\partial x_2}\Delta x_2\right)^2+\cdots+\left(\frac{\partial f}{\partial x_n}\Delta x_n\right)^2}\]označovaný zákon šíření chyb.
4.8. Zákon šíření chyb (příklad)#

Obr. 4.2 Pocitová teplota v zimě závisí na skutečné teplotě a na síle větru. Zdroj: pixabay.com#
Kanadský empirický vzorec pro pocitovou teplotu v zimě (wind-chill factor) je
Dosazením do vzorce dostáváme \(\displaystyle W(-11,26)=-20.212\,{}^\circ\!\text{C}\). Derivováním dostáváme
4.9. Z ptačí perspektivy#

Obr. 4.3 Ještě pohled s trochou nadhledu. Zdroj: pixabay.com#
Rotace vektorového pole je další z diferenciálních operátorů. Význam tohoto operátoru nespatřujeme v jeho základním určení, které mu dalo název a srozumitelnou interpretaci (roztáčí unášené objekty okolo své osy), ale v jeho souvislosti s existencí skalárního potenciálu vektorového pole.
Ve dvourozměrné formulaci je nulovost rotace nutná a současně postačující podmínka k možnosti zavedení skalárního potenciálu. V takovém případě je možno přejít od vektorového popisu pole ke skalárnímu popisu (skalární je jednodušší).
Rotace je jedním z vyjadřovacích prostředků, které použijeme později pro formulaci Greenovy věty. Ta zprostředkovává přechod mezi difuzní rovnicí v bodě (v nekonečně malém objemu) a bilancí stavové veličiny v měřitelném makroskopickém tělese.
V závěru přednášky, bez souvislosti s operátorem rotace, jsme se seznámili s dovedností analyzovat vliv nepřesností ve vstupních datech na nepřesnost na výstupu. Zákon šíření chyb umožní naplánovat experiment zaměřený na stanovení nepřímo měřené veličiny a umožní identifikovat ty části procesu, které podstatně ovlivňují spolehlivost výsledku.