11. Lineární diferenciální rovnice druhého řádu

Anotace.

• Lineární diferenciální rovnice druhého řádu se vyskytují v úlohách z mechaniky a při řešení difuzní rovnice.

• Soustřeďte se na vysvětlení, jak souvisí DR druhého řádu se zrychlením tělesa a působící silou v úlohách z mechaniky, jak se může jednorozměrná difuzní stacionární rovnice redukovat na LDR druhého řádu a jak se metodou separace proměnných dá nestacionární difuzní rovnice rozdělit na obyčejnou diferenciální rovnici prvního a druhého řádu.

• Soustřeďte se na pasáže týkající se toho, jak okrajová podmínka dokáže vybrat hodnoty parametrů, pro které existuje nenulové řešení. To determinuje například frekvenci při mechanickém kmitání.

• Numerické experimenty s rovnicí. Konkrétní nalezení řešení rovnice pomocí řešení kvadratické rovnice, pomocí metody neurčitých koeficientů pro nalezení partikulárního řešení atd. je pro nás málo zajímavé a věnujte se mu případně až v poslední fázi.

11.1. Lineární diferenciální rovnice druhého řádu

Video

Definice (Lineární diferenciální rovnice druhého řádu)

Buďte \(\displaystyle p\), \(\displaystyle q\) a \(\displaystyle f\) funkce definované a spojité na intervalu \(\displaystyle I\). Diferenciální rovnice

(11.1)\[y''+p(x)y'+q(x)y=f(x) \]

se nazývá lineární diferenciální rovnice druhého řádu. Řešením rovnice (nebo též integrálem rovnice) na intervalu \(\displaystyle I\) rozumíme funkci, která má spojité derivace do řádu \(\displaystyle 2\) na intervalu \(\displaystyle I\) a po dosazení identicky splňuje rovnost (11.1) na \(\displaystyle I\). Úloha nalézt řešení rovnice, které splňuje v bodě \(\displaystyle x_0\in I\) počáteční podmínky

(11.2)\[\begin{split}\begin{aligned}y(x_0)&=y_0,\\ y'(x_0)&=y'_0,\end{aligned}\end{split}\]

kde \(\displaystyle y_0\) a \(\displaystyle y'_0\) jsou reálná čísla, se nazývá počáteční úloha (Cauchyova úloha). Řešení počáteční úlohy se nazývá partikulární řešení rovnice.

Zkratky: LDE - lineární diferenciální rovnice, IC - počáteční podmínka, IVP - počáteční úloha

11.2. Příklad - těleso na pružině

Obr. 11.1 Těleso na pružině je nejjednodušší model pro rovnice druhého řádu. Přesto není vhodné tento model podceňovat, dokáže být velmi užitečný i u jiných úloh, které se týkají oscilací. Chemické oscilace, považované za základ tzv. buněčných hodin i jiných vnitřních cyklů biologických organismů, jsou ale založeny na jiném popisu. (Viz Brusselator.) Zdroj: pixabay.com

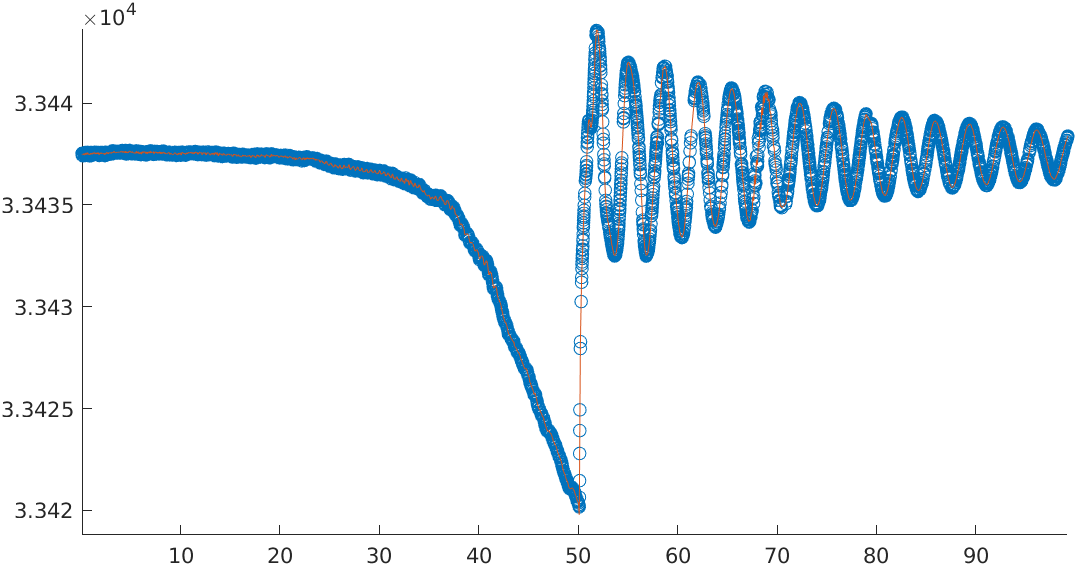
Obr. 11.2 Vlastní kmity bodu na kmeni stromu ve výšce 4m po vychýlení stromu z rovnovážné polohy a vypuštění. Až na úvodní pasáž v čase cca 52 sekund výchylka odpovídá tlumenému kmitání tělesa na pružině. Zdroj: projekt DYNATREE

Kmity tělesa o hmotnosti \(\displaystyle m\) pružně připevněného k nehybné podložce spojem tuhosti \(\displaystyle k\) jsou popsány diferenciální rovnicí \(\displaystyle {\ddot x+\frac km x=0}.\) Zde navíc používáme fyzikální úzus označovat derivace podle času pomocí tečky a ne čárky. Symbol \(\displaystyle \ddot x\) tedy značí druhou derivaci funkce \(\displaystyle x\), kde \(\displaystyle x\) bereme jako funkci času.

Jednoduchým mechanickým modelem je těleso na pružině. Zde je deformace úměrná působící síle. Analogické situace vedoucí na stejnou rovnici však dostáváme i obecněji. Pokud pro jednoduchost předpokládáme, že těleso s jedním stupněm volnosti se nachází ve stabilním stavu s minimem potenciální energie a energie závisí na poloze \(\displaystyle x\), můžeme v okolí minima \(\displaystyle x_0\) potenciální energii aproximovat Taylorovým rozvojem druhého řádu

\[E(x)\approx E(x_0)+E'(x_0)(x-x_0)+\frac 12E''(x_0)(x-x_0)^2.\]

Vzhledem k tomu, že v \(\displaystyle x_0\) je minimum, platí \(\displaystyle E'(x_0)=0\). Je výhodné volit počátek v rovnovážné poloze, protože poté platí \(\displaystyle x_0=0\). Síla je poté dána vztahem

\[F(x)=-\frac{\partial}{\partial x}E(x)=-E''(0)x.\]

Síla \(\displaystyle F\) je tedy úměrná výchylce \(\displaystyle x\) a vrací těleso do rovnovážné polohy.

Situace tedy perfektně koresponduje s kmitáním na pružině i když potenciální energie uvažovaná v tomto odstavci může být jiného charakteru. Něco podobného jsme viděli již u autonomních systémů, kdy systém modelující tlumený oscilátor z přednášky byl stejný jako systém modelující regulaci topení ze cvičení a tento systém byl jenom lépe představitelnou realizací systému regulace syntézy proteinů.

11.3. Řešitelnost LDE druhého řádu

Video

Budeme se zabývat řešitelností diferenciální rovnice (11.1), tj. rovnice

\[y''+p(x)y'+q(x)y=f(x).\]

Věta (o existenci a jednoznačnosti řešení LDE druhého řádu)

Každá počáteční úloha pro LDE druhého řádu má řešení, které je určeno jednoznačně a toto řešení je definované na celém intervalu \(\displaystyle I\).

Definice (speciální typy LDE druhého řádu)

Platí-li v rovnici (11.1) \(\displaystyle f(x)=0\) pro všechna \(\displaystyle x\in I\), nazývá se rovnice (11.1) homogenní, v opačném případě nehomogenní.

Jsou-li koeficienty \(\displaystyle p(x)\) a \(\displaystyle q(x)\) na intervalu \(\displaystyle I\) konstantní funkce, nazývá se (11.1) rovnice s konstantními koeficienty.

Definice (triviální řešení)

Funkce \(\displaystyle y(x)\equiv 0\) je řešením homogenní LDE druhého řádu

\[y''+p(x)y'+q(x)y=0\]

vždy, bez ohledu na tvar koeficientů \(\displaystyle p\), \(\displaystyle q\). Toto řešení nazýváme triviální řešení.

Definice (asociovaná homogenní rovnice)

Nahradíme-li v nehomogenní LDE pravou stranu (tj. funkci \(\displaystyle f\)) nulovou funkcí, obdržíme rovnici

\[ y''+p(x)y'+q(x)y=0.\]

Tato rovnice se nazývá asociovaná homogenní rovnice k rovnici (11.1).

Definice (obecné řešení)

Všechna řešení LDE druhého řádu lze vyjádřit ve tvaru obsahujícím dvě nezávislé konstanty \(\displaystyle C_1\), \(\displaystyle C_2\in\mathbb{R}\). Takovýto předpis se nazývá obecné řešení rovnice (11.1).

11.4. Důsledky linearity

Nechť \(\displaystyle L\) je lineární diferenciální operátor druhého řádu. Jako speciální případ vztahu

\[L[C_1y_1+C_2y_2]=C_1L[y_1]+C_2L[y_2]\]

dostáváme následující.

• Platí

  \[L[y_1]=L[y_2]=0\ \implies \ L[C_1y_1+C_2y_2]=0,\]
  tj. každá lineární kombinace dvou řešení homogenní LDE je opět řešením této rovnice. Pokud se nám navíc podaří volbou konstant \(\displaystyle C_1\) a \(\displaystyle C_2\) splnit libovolnou počáteční podmínku, je jistota, že máme obecné řešení.

• Platí

  \[L[y_2]=0 \text{ a } L[y_1]=f(x)\ \implies\ L[y_1+y_2]=f(x),\]
  tj. součet řešení nehomogenní a asociované homogenní LDE je řešením původní nehomogenní rovnice. Pokud je navíc \(\displaystyle y_2\) obecným řešením homogenní rovnice, je \(\displaystyle y_1+y_2\) obecným řešením nehomogenní rovnice, protože se podaří splnit libovolnou počáteční podmínku.

11.5. Důsledky linearity prakticky

Vztah

\[L[C_1y_1+C_2y_2]=C_1L[y_1]+C_2L[y_2]\]

poslouží (podobně jako u lineárních rovnic prvního řádu), abychom popsali strukturu množiny všech řešení rovnice a dokázali tuto množinu vytvořit jenom na základě znalosti několika prvků.

Rovnice

(11.3)\[y''+y=x\]

má partikulární řešení \(\displaystyle y=x\).

Asociovaná homogenní rovnice je

(11.4)\[y''+y=0.\]

Tato rovnice má řešení například \(\displaystyle y=\sin x\), \(\displaystyle y=\cos x\). Z linearity plyne

• Funkce \(\displaystyle y=C_1 \sin x+C_2 \cos x\) je řešením rovnice (11.4) pro libovolná reálná \(\displaystyle C_1\), \(\displaystyle C_2\). Protože platí \(\displaystyle y(0)=C_2\) a \(\displaystyle y'(0)=C_1\), je možné splnit libovolnou podmínku \(\displaystyle y(0)=\alpha\), \(\displaystyle y'(0)=\beta\) volbou \(\displaystyle C_2=\alpha\) a \(\displaystyle C_1=\beta\). Jedná se tedy o obecné řešení.

• Funkce \(\displaystyle y=C_1 \sin x+C_2\cos x +x\) je obecným řešením rovnice (11.4).

11.6. Homogenní LDE 2. řádu (obecné řešení)

(11.5)\[y''+p(x)y'+q(x)y=0 \]

Věta (obecné řešení homogenní LDE)

Jsou-li \(\displaystyle y_1\) a \(\displaystyle y_2\) dvě netriviální lineárně nezávislá řešení rovnice (11.5) na intervalu \(\displaystyle I\), pak funkce \(\displaystyle y\) definovaná vztahem

\[ y(x, C_1, C_2)=C_1y_1(x)+C_2y_2(x),\]

kde \(\displaystyle C_{1,2}\in\mathbb{R}\), je obecným řešením rovnice (11.5) na intervalu \(\displaystyle I\).

Dvojicí lineárně nezávislých řešení rozumíme taková dvě řešení, že jedno není násobkem druhého.

Definice (fundamentální systém řešení)

Dvojici funkcí \(\displaystyle y_1\) a \(\displaystyle y_2\) z předchozí věty nazýváme fundamentální systém řešení rovnice (11.5).

11.7. Homogenní LDE 2. řádu s konstantními koeficienty

Rovnici

\[y''+py'+qy=0\]

je možno přepsat na

\[(y')^\prime=-qy-py'\]

a tato rovnice je po substituci \(\displaystyle x_1=y\), \(\displaystyle x_2=y'\) ekvivalentní autonomnímu systému

\[\begin{split}\begin{pmatrix}x_1\\x_2\end{pmatrix}'=\begin{pmatrix}0 &1\\ -q &-p\end{pmatrix} \begin{pmatrix}x_1\\x_2\end{pmatrix} \end{split}\]

U řešitelnosti této rovnice hraje velkou roli charakteristická rovnice matice soustavy, která je obsažena v následující definici.

Definice (charakteristická rovnice)

Kvadratická rovnice

\[z^2+pz+q=0\]

s neznámou \(\displaystyle z\) se nazývá charakteristická rovnice pro rovnici

\[y''+py'+qy=0.\]

Věta (o obecném řešení LDE s konstantními koeficienty)

Uvažujme LDE

(11.6)\[y''+py'+qy=0,\]

a její charakteristickou rovnici

\[z^2+pz+q=0.\]

• Jsou-li \(\displaystyle z_1,z_2\in\mathbb{R}\) dva různé reálné kořeny charakteristické rovnice, definujme

  \[{y_1=e^{z_1 x}}, \qquad{y_2=e^{z_2 x}}.\]

• Je-li \(\displaystyle z_1\in\mathbb{R}\) dvojnásobným kořenem charakteristické rovnice, definujme

  \[{y_1=e^{z_1 x}}, \qquad{y_2=xe^{z_1 x}}.\]

• Jsou-li \(\displaystyle z_{1,2}=\alpha\pm i\beta\not\in\mathbb{R}\) dva komplexně sdružené kořeny charakteristické rovnice, definujme

  \[{y_1(x)=e^{\alpha x}\cos(\beta x)}, \qquad {y_2(x)=e^{\alpha x}\sin(\beta x)}.\]

Potom obecné řešení rovnice (11.6) je

\[y(x,C_1,C_2)=C_1y_1(x)+C_2y_2(x),\qquad C_1\in\mathbb{R},\ C_2\in\mathbb{R}.\]

11.8. Nehomogenní LDE 2. řádu

Věta (o obecném řešení nehomogenní LDE)

Součet libovolného partikulárního řešení nehomogenní lineární diferenciální rovnice a obecného řešení asociované homogenní rovnice je obecným řešením původní nehomogenní rovnice

Následující věta udává jednu z metod nalezení partikulárního řešení, pokud je diferenciální rovnice do jisté míry speciální: má konstantní koeficienty a polynomiální pravou stranu.

Věta (metoda neurčitých koeficientů)

Uvažujme lineární diferenciální rovnici druhého řádu

\[y''+py'+qy=P_n(x),\]

kde \(\displaystyle p\in\mathbb{R}\) je konstanta, \(\displaystyle q\in\mathbb{R}\setminus\{0\}\) je nenulová konstanta a \(\displaystyle P_n(x)\) je polynom stupně \(\displaystyle n\). Existuje polynom stupně \(\displaystyle n\), který je partikulárním řešením této diferenciální rovnice.

V praxi polynom, který má být řešením, napíšeme s neurčitými koeficienty a dosazením do rovnice určíme potřebné hodnoty těchto koeficientů.

11.9. Dirichletova okrajová úloha, vlastní čísla

Video

Někdy je nutné řešit diferenciální rovnice druhého řádu s jinými než počátečními podmínkami. Ukážeme si na jednoduchém příkladě odlišnost od počáteční úlohy. Následující úloha má velké uplatnění při studiu kmitavých pohybů.

Pro parametr \(\displaystyle \lambda\in\mathbb{R}\) najděte řešení rovnice

(11.7)\[y''+\lambda y=0 \]

splňující podmínky

(11.8)\[y(0)=0=y(1). \]

Definice (okrajová úloha)

Úloha najít řešení diferenciální rovnice (11.7), které splňuje podmínky (11.8) se nazývá (Dirichletova) okrajová úloha.

Odlišnost Dirichletovy úlohy od (Cauchyovy) počáteční úlohy je v tom, že nezadáváme funkční hodnotu a derivaci v jednom bodě, ale funkční hodnotu ve dvou různých bodech.

Jedno z řešení Dirichletovy úlohy je triviální řešení \(\displaystyle y(x)=0\). Ukazuje se, že netriviální řešení existuje jen pro některé hodnoty parametru \(\displaystyle \lambda\).

Definice (vlastní funkce, vlastní hodnota okrajové úlohy)

Hodnota \(\displaystyle \lambda\), pro kterou existuje netriviální řešení Dirichletovy okrajové úlohy, se nazývá vlastní hodnota okrajové úlohy a příslušné řešení se nazývá vlastní funkce okrajové úlohy.

11.10. Výpočet vlastních hodnot

11.10.1. Případ \(\displaystyle \lambda>0\)

Je-li \(\displaystyle \lambda>0\), je řešením rovnice

\[y''+\lambda y=0 \]

funkce

\[y(x)=C_1\sin(\sqrt \lambda x)+C_2\cos(\sqrt \lambda x).\]

Z podmínky \(\displaystyle y(0)=0\) dostáváme \(\displaystyle C_2=0\). Tedy

\[y(x)=C_1\sin(\sqrt\lambda x).\]

Z podmínky \(\displaystyle y(1)=0\) dostáváme

\[0=C_1\sin(\sqrt\lambda),\]

která je splněna pokud \(\displaystyle C_1=0\), nebo \(\displaystyle \sqrt\lambda=k\pi\), \(\displaystyle k\in\mathbb{Z}\)

Okrajová úloha

\[y''+\lambda y=0, \quad y(0)=0=y(1)\]

má vlastní hodnoty \(\displaystyle \lambda=(k\pi)^2\), \(\displaystyle k\in\mathbb{Z}\)

11.10.2. Případ \(\displaystyle \lambda<0\)

Je-li \(\displaystyle \lambda<0\), je řešením rovnice

\[y''+\lambda y=0\]

funkce

\[y(x)=C_1e^{\sqrt {-\lambda} x}+C_2 e^{-\sqrt {-\lambda} x}.\]

Z podmínky \(\displaystyle y(0)=0\) dostáváme

\[C_1+C_2=0.\]

Z podmínky \(\displaystyle y(1)=0\) dostáváme

\[C_1e^{\sqrt {-\lambda}}+C_2 e^{-\sqrt {-\lambda}}=0.\]

Protože jedna rovnice není násobkem druhé, má soustava jediné řešení \(\displaystyle C_1=C_2=0\) a okrajová úloha má v případě \(\displaystyle \lambda<0\) pouze triviální nulové řešení. Nemá tedy žádné vlastní hodnoty.

11.10.3. Obvyklá formulace

V praktických úlohách, kdy požadujeme existenci nenulového řešení, zpravidla pracujeme s rovnicí ve tvaru

\[y''+\lambda^2 y=0,\]

abychom zdůraznili kladnou hodnotu parametru a abychom dostávali řešení formálně bez druhé odmocniny. Tedy okrajová úloha

\[y''+\lambda^2 y=0,\quad y(0)=0=y(1)\]

má vlastní čísla \(\displaystyle \lambda=k\pi\), kde \(\displaystyle k\) je kladné celé číslo.

11.11. Kmity struny

Obr. 11.3 Kmitání jednorozměrných objektů je popsáno lineární diferenciální rovnicí druhého řádu. Zdroj: pixabay.com

Při kmitání struny délky \(\displaystyle l\) upevněné na koncích se ukazuje, že proces je možno modelovat okrajovou úlohou

\[y''+\lambda^2 y=0,\quad y(0)=0=y(l),\]

kde \(\displaystyle y\) je amplituda kmitů v místě \(\displaystyle x\) a \(\displaystyle \lambda\) souvisí s frekvencí. Rovnice má obecné řešení

\[y(x)=C_1\sin( \lambda x)+C_2\cos( \lambda x)\]

Z podmínky \(\displaystyle y(0)=0\) dostáváme \(\displaystyle C_2=0\) a z podmínky \(\displaystyle y(l)=0\) dostáváme

\[y(x)=C_1\sin(\lambda x)\]

pokud

(11.9)\[\lambda l=k\pi \]

a \(\displaystyle y=0\) jinak. Při podrobnějším popisu se ukazuje, že \(\displaystyle \lambda\) souvisí s hmotností struny, napětím ve struně a frekvencí, kterou slyšíme. Podmínka (11.9) určuje spektrum slyšitelných frekvencí, na kterých může struna kmitat, výsledný pohyb (a zvuk) je díky linearitě složením jednotlivých variant. Toho se dá s výhodou vyžívat a stejnou strunu je možné rozeznívat více způsoby a dosahovat různý výsledný zvuk.

11.12. Vzpěry

Obr. 11.4 Nosníky, ať už samostatné vzpěry, nebo součásti příhradových konstrukcí, je nutné posuzovat i z hlediska axiálního namáhání. Ignorování tohoto způsobu namáhání vedlo v 19. století k pádu několika příhradových železničních mostů a následnému stržení řady chybně dimenzovaných mostů. Zdroj: pixabay.com

Předpokládejme, že máme nosník namáhaný na vzpěr. Nosník je uchycen na dolním a horním konci tak, že se nemůže pohybovat do stran, ale může se otáčet. Osu \(\displaystyle x\) zvolíme podélně v ose vzpěry, osu \(\displaystyle y\) kolmo. Při namáhání takového nosníku je výchylka dána okrajovou úlohou (A. Požgaj a kol., Štruktúra a vlastnosti dreva, str. 359)

\[\frac{\mathrm d^2 y}{\mathrm dx^2}+\alpha^2 y=0,\quad y(0)=y(l)=0,\]

kde \(\displaystyle \alpha^2=\frac{F}{EI}\) je parametr závislý na působící síle, materiálu a kvadratickém momentu průřezu nosníku. (Pro jiné způsoby uchycení se rovnice a okrajové podmínky mohou mírně lišit, rovnice může být například i nehomogenní a pro jiné druhy zatížení i vyššího řádu, zásadní vlastnosti jsou však stejné.) Toto je stejná úloha jako u kmitání struny. Při síle, která se postupně zvětšuje, se nenulové řešení objeví v bodě, kde platí

\[\alpha l=\pi,\]

(odpovídá základní frekvenci struny) tj.

\[\sqrt{\frac {F}{EI}}l=\pi\]

a

\[F=\frac{\pi^2 EI}{l^2}.\]

Toto je pro daný nosník kritická síla a ta je pro daný materiál nepřímo úměrná druhé mocnině délky a přímo úměrná kvadratickému momentu \(\displaystyle I\).

11.13. Neumannova a smíšená okrajová úloha

Obr. 11.5 Array mbira - hudební nástroj se smíšenou okrajovou úlohou

Při řešení Dirichletovy úlohy hledáme řešení diferenciální rovnice druhého řádu s předepsanými hodnotami ve dvou různých bodech

\[y(a)=\alpha,\quad y(b)=\beta.\]

Tento požadavek se uplatní při studiu kmitů struny nebo tyče s pevnými konci.

V praxi je možné si představit i jiné podmínky. Například v termodynamice se používají podmínky na hodnotu derivací ve dvou různých bodech

\[y'(a)=\alpha, \quad y'(b)=\beta.\]

Takové podmínky se nazývají Neumannovy podmínky a úloha najít řešení rovnice, které tyto podmínky splňuje, se nazývá Neumannova okrajová úloha, též Neumannova úloha.

Existují i smíšené úlohy, například při kmitání tělesa s jedním upevněným a jedním volným koncem je přirozené formulovat smíšenou okrajovou podmínku

\[y(a)=0,\quad y'(b)=0,\]

kde \(\displaystyle a\) je upevněný konec a \(\displaystyle b\) volný konec.

11.14. Fourierova metoda separace proměnných

Video

Budeme se zabývat jednorozměrnou rovnicí vedení tepla ve tvaru

\[\frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial x^2}.\]

V tomto tvaru rovnice neobsahuje žádné konstanty a je to tvar, se kterým se pracuje ve většině matematických publikací. Reálnou rovnici vedení tepla převedeme do tohoto tvaru zavedením bezrozměrných veličin, což si ukážeme v následující přednášce. Teď si ukážeme, jak řešení rovnice vede na řešení LDR druhého řádu. Uvažujme pro jednoduchost okrajovou úlohu, kdy konce tyče jsou udržovány na nulové teplotě, tj. je-li tyč délky \(\displaystyle l\) položena v ose \(\displaystyle x\) tak, že levý konec je v počátku, platí pro teplotu \(\displaystyle u(x,t)\) podmínky \(\displaystyle u(0,t)=u(l,t)=0\) v libovolném čase \(\displaystyle t\).

Budeme řešení hledat ve tvaru \(\displaystyle u(x,t)=\varphi(x)\psi(t)\), kde \(\displaystyle \varphi\) a \(\displaystyle \psi\) jsou funkcemi jedné proměnné. Platí

\[\frac{\partial u}{\partial t}=\varphi(x)\psi'(t), \quad \frac{\partial^2 u}{\partial x^2}=\varphi''(x) \psi(t)\]

a rovnice má tvar

\[\varphi(x)\psi'(t)=\varphi''(x)\psi (t).\]

Vydělením této rovnice součinem \(\displaystyle \varphi(x)\psi(t)\) dostáváme

\[\frac {\psi'(t)}{\psi(t)}=\frac{\varphi''(x)}{\varphi (x)}.\]

Toto je rovnice, kde levá strana je funkcí proměnné \(\displaystyle t\) a pravá strana funkcí proměnné \(\displaystyle x\). Obě proměnné jsou však nezávislé a uvedená rovnost může být splněna jen tehdy, když se rovnají společné konstantě.

\[\frac {\psi'(t)}{\psi(t)}=\frac{\varphi''(x)}{\varphi (x)}=\omega.\]

Okrajové podmínky vynucují platnost vztahů \(\displaystyle \varphi(0)=\varphi(l)=0\). Jesliže je v takovém případě konstanta \(\displaystyle \omega\) kladná, má úloha pouze nulové řešení (viz výše výpočet vlastních hodnot pro tuto úlohu). Konstanta \(\displaystyle \omega\) tedy musí být záporná. Přeznačme ji do tvaru

\[\omega = -\lambda^2\]

Platí tedy

\[\frac {\psi'(t)}{\psi(t)}=-\lambda ^2,\quad \frac{\varphi''(x)}{\varphi (x)}=-\lambda ^2.\]

První rovnice představuje lineární diferenciální rovnici prvního řádu

\[\psi'=-\lambda^2\psi\]

s partikulárním řešením \(\displaystyle \psi(t)=e^{-\lambda^2 t}.\) Druhá rovnice představuje společně s okrajovou podmínkou okrajovou úlohu pro lineární diferenciální rovnici druhého řádu

\[\varphi''+\lambda^2\varphi=0, \quad \varphi(0)=\varphi(l)=0.\]

Máme tedy Dirichletovu úlohu na vlastní čísla a vlastní funkce, jak jsme ji viděli u kmitů struny nebo u namáhání na vzpěr. Řešením je funkce \(\displaystyle \varphi(x)=\sin(\lambda x)\), kde \(\displaystyle \lambda\) je vlastní hodnota této úlohy. Funkce

\[u(x,t)=\sin(\lambda x)e^{-\lambda^2 t}\]

je tedy řešením rovnice

\[\frac{\partial u}{\partial t}=\frac{\partial^2 u}{\partial x^2}.\]

Rovnici je možno přepsat do tvaru

\[\frac{\partial u}{\partial t}-\frac{\partial^2 u}{\partial x^2}=0,\]

kdy na levé straně stojí lineární operátor a na pravé straně je nula. Proto je každá lineární kombinace řešení opět řešením a pro libovolnou volbu konstant je funkce

\[u(x,t)=\sum_{\lambda}C_\lambda\sin(\lambda x)e^{-\lambda^2 t}\]

také řešením. Součet na pravé straně je přes všechna vlastní čísla, kterých je nekonečně mnoho.

Nyní začíná být rozbor úlohy nad rámec našeho kurzu, protože se objevil nekonečný součet. Ukazuje se, že tento zápis je dostatečně bohatý na to, aby obsáhl libovolnou rozumnou počáteční podmínku a vzorec je tedy schopen popsat řešení úlohy pro libovolné fyzikálně relevantní situace. Vidíme i přímo strukturu řešení, které je jakousi lineární kombinací různých módů. Tato skutečnost lépe vynikne na analogické diferenciální rovnici kmitání struny, kdy jednotlivé módy přímo vnímáme sluchem: struna nemůže kmitat na libovolné frekvenci, ale pouze a frekvenci dané okrajovou podmínkou a na frekvencích násobných.

Poznámka: Podobná situace a možnost separace proměnných je u rovnice kmitů struny

\[\frac{\partial^2 u}{\partial t^2}=\frac{\partial^2 u}{\partial x^2}\]

nebo jejího zobecnění na kmity desek a chvění těles. Opět separace vede k LDR druhého řádu pro složku závisející na \(\displaystyle x\). V tomto případě je druhého řádu i rovnice pro složku závislou na čase.