2. Gradient

Anotace.

• V úvodu si osaháme gradient a jeho využití k lineární aproximaci a jeho vztah k vrstevnicím.

• Komplexnější je pátý příklad. Ukazuje mimo jiné, že někdy je výhodnější řešit úlohu v rámci obecnější teorie.

• V šestém příkladě si ilustrujeme na příkladě linearizaci vektorové funkce v počátku. Tato linearizace je v podstatě cesta k jednotné formulaci konstitučních zákonů. Ukázku použití takového zákona si představíme v sedmém příkladě.

• Poslední příklad nás zavede do světa zpracování reálných dat a vyzkoušíme si nalezení gradientu numerickou cestou.

2.1. Linearizace pocitové teploty

Video

Obr. 2.15 Zdroj: pixabay.com

Pocitová teplota \(\displaystyle W\) z minulého cvičení má v bodě odpovídajícím teplotě \(\displaystyle T=-11{}^\circ\mathrm C\) a rcyhlosti větru \(\displaystyle v=26\,\mathrm {km}\,\mathrm{hod}^{-1}\) má hodnotu

\[W=-20.2 ^\circ\mathrm C\]

a parciální derivace

\[\pdv{W}{v}=-0.163 ^\circ\mathrm C\, \mathrm {hod}\,\mathrm{km}^{-1}\]

a

\[\pdv{W}{T}=1.289.\]

Najděte pomocí lineární aproximace vzorec pro pocitovou teplotu v okolí tohoto bodu.

Řešení

Přímým použitím vzorce pro lineární aproximaci dostáváme

\[ W=-20.2+1.289(T-(-11))-0.163(v-26)=-20.2+1.289(T+11)-0.163(v-26), \]

přičemž všechny veličiny dostazujeme v jednotkách SI (stupně Celsia a kilometry za hodinu).

2.2. Parciální derivace, gradient

Video

Určete gradient funkcí \(\displaystyle z=ax^2y-2xy^2\) a \(\displaystyle h=\frac {ax}{y^2}+5x^3y^2\), kde \(\displaystyle a\in\mathbb R\) je reálný parametr.

Řešení

\[\begin{split} \begin{aligned} \pdv{z}{x} &= 2axy-2y^2\\ \pdv{z}{y} &= ax^2-4xy\\ \nabla z &= (2axy-2y^2, ax^2-4xy) = (2axy-2y^2)\vec \imath + (ax^2-4xy)\vec \jmath\\ \pdv{h}{x} &= \frac a{y^2}+15x^2y^2\\ \pdv{h}{y} &= ax(-2)y^{-3}+10x^3y=-\frac{2ax}{y^3}+10x^3y\\ \nabla h &= \left(\frac a{y^2}+15x^2y^2, -\frac{2ax}{y^3}+10x^3y\right) = \left(\frac a{y^2}+15x^2y^2\right)\vec \imath + \left(-\frac{2ax}{y^3}+10x^3y\right)\vec \jmath \end{aligned} \end{split}\]

2.3. Gradient funkce s vrstevnicemi ve tvaru kružnic

Video

Určete gradient funkce \(\displaystyle z=x^2+y^2\) a zkontrolujte, že je v každém bodě kolmý ke kružnici se středem v počátku. Využijte toho, že spojnice bodu na kružnici se středem kružnice je kolmá k této kružnici.

Řešení

\[\begin{split}\begin{aligned} \pdv{z}{x} &= 2x\\ \pdv{z}{y} &= 2y\\ \nabla z &= (2x, 2y) = 2x\vec \imath + 2y\vec \jmath \end{aligned}\end{split}\]

Vektor \(\displaystyle (2x,2y)\) v bodě \(\displaystyle (x,y)\) míří směrem od počátku, tj ve směru spojnice se středem a tedy je kolmý k vrstevnici.

2.4. Gradient funkce s paprskovitými vrstevnicemi

Video

Určete gradient funkce \(\displaystyle z=\mathop{\mathrm{arctg}} \frac yx\) a zkontrolujte, že je v každém bodě tečný ke kružnici se středem v počátku. Využijte toho, že tečna je kolmá na poloměr.

Řešení

\[\begin{split} \begin{aligned} \pdv{z}{x} &= \frac1{1+\frac {y^2}{x^2}}y\frac {(-1)}{x^2}=-\frac{y}{x^2+y^2}\\ \pdv{z}{y} &= \frac1{1+\frac {y^2}{x^2}}\frac 1x=\frac{x}{x^2+y^2}\\ \nabla z &= \left(-\frac{y}{x^2+y^2},\frac{x}{x^2+y^2}\right)= \frac{1}{x^2+y^2} (-y,x) \end{aligned} \end{split}\]

Vektor \(\displaystyle (-y,x)\) v bodě \(\displaystyle (x,y)\) je kolmý k vektoru \(\displaystyle (x,y)\). Proto je tečný ke kružnici.

2.5. Tečná rovina atd.

Video

Pro funkci \(\displaystyle f(x,y)=x^2+\frac x{y^2}-6\) najděte

1. gradient,

2. gradient v bodě \(\displaystyle (2,1)\),

3. lineární aproximaci v bodě \(\displaystyle (2,1)\),

4. tečnou rovinu v bodě \(\displaystyle (2,1)\),

5. rovnici vrstevnice bodem \(\displaystyle (2,1)\) a rovnici tečny k vrstevnici tímto bodem,

6. explicitní vyjádření funkce dané v okolí bodu \(\displaystyle (2,1)\) implicitně rovnicí \(\displaystyle f(x,y)=0\),

7. lineární aproximace v okolí bodu \(\displaystyle x=2\) pro funkci získanou v předchozím bodu.

V tomto příkladě ukazujeme, že někdy je vhodné úlohu řešit v rámci obecnější teorie. Zde v podúkolu číslo 7 vlastně najdeme lineární aproximaci relativně komplikované funkce jedné proměnné (nalezené v podúkolu 6). To se dá udělat prostředky diferenciálního počtu funkcí jedné proměnné, ale výpočet by byl poměrně nepříjemný, protože by bylo nutno derivovat funkci s nepříjemnou odmocninou. Alternativa je najít tečnou rovinu k funkci více proměnných z našeho zadání a příslušný řez této tečné roviny bude tečnou k vrstevnici. Použitý aparát je sice pokročilejší (používáme funkce více proměnných tam, kde by stačily funkce jedné proměnné), ale početní náročnost je nižší. Technicky je derivování nepříjemné odmocniny ze zlomku nahrazeno derivováním polynomu.

Řešení

1. \(\displaystyle \nabla f=\left(2x+\frac 1{y^2},-2\frac x{y^3}\right)\)

2. \(\displaystyle \nabla f(2,1)=(5,-4)\)

3. \(\displaystyle f(x,y)\approx 5(x-2)-4(y-1)\)

4. \(\displaystyle z= 5(x-2)-4(y-1)\)

5. Rovnice vrstevnice je

   \[x^2+\frac x{y^2}-6=0\]
   a tečna
   \[5(x-2)-4(y-1)=0,\]
   tj.
   \[5x-4y-6=0.\]

6. Postupnými úpravami a výběrem správného znaménka po vyřešení kvadratické rovnice vzhledem k \(\displaystyle y\) dostáváme

   \[\begin{split} \begin{aligned} x^2+\frac x{y^2}-6&=0\\ \frac x{y^2}&=6-x^2\\ y^2&=\frac{x}{6-x^2}\\ y&=\sqrt{\frac{x}{6-x^2}}\\ \end{aligned} \end{split}\]

7. Z rovnice tečny k vrstevnici

   \[5(x-2)-4(y-1)=0\]
   dostáváme
   \[y=1+\frac 54 (x-2)\]
   a proto
   \[\sqrt{\frac{x}{6-x^2}}\approx 1+\frac 54 (x-2)\]
   v okolí \(\displaystyle x=2\). Všimněte si, že jsme nepotřebovali aproximovanou funkci \(\displaystyle \sqrt{\frac{x}{6-x^2}}\) vůbec derivovat. To je výhoda, protože derivace odmocniny z podílu se nepočítá zcela příjemně. Namísto toho jsme využili výsledek z teorie funkce více proměnných. Přitom se musela využít nadřazená teorie, ale k výpočtu nebylo třeba derivovat nic horšího, než mocninnou funkci.

Testová otázka Testová otázka Testová otázka Testová otázka

2.6. Linearizace vektorové funkce, Jacobiho matice

Video

Jacobiho matice se používá k linearizaci vektorových funkcí, které mají na vstupu i na výstupu uspořádanou n-tici. Jsou to matice, kde gradienty jednotlivých komponent vektorové funkce jsou zapsány do řádků matice.

Najděte Jacobiho matici pro funkci

\[\vec F(x,y)=(x^2+xy+6y)\vec i + e^{3x}\vec j\]

a poté hodnotu této matice v bodě \(\displaystyle (0,0)\).

Řešení

Platí

\[\begin{split}\begin{aligned} \frac{\partial }{\partial x}\left(x^2 +xy+6y\right) &=2x+y\\ \frac{\partial }{\partial y}\left(x^2 +xy+6y\right) &=x+6\\ \frac{\partial }{\partial x}\left(e^{3x}\right) &=3e^{3x}\\ \frac{\partial }{\partial y}\left(e^{3x}\right) &=0\\ \end{aligned}\end{split}\]

a proto má Jacobiho matice tvar

\[\begin{split} J(x,y)= \begin{pmatrix} 2x+y & x+6\\ 3e^{3x} & 0 \end{pmatrix}. \end{split}\]

V bodě \(\displaystyle (0,0)\) potom platí

\[\begin{split} J(0,0)= \begin{pmatrix} 0 & 6\\ 3 & 0 \end{pmatrix}. \end{split}\]

Testová otázka Testová otázka

2.7. Parciální derivace, gradient a násobení matic

Video

Obr. 2.16 Zdroj: Wood handbook

Vypočtěte gradient funkce

\[T=10-\sqrt{x^2+y^2}\]

definující teplotu ve dvourozměrném materiálu. Ukažte, že vrstevnice této funkce jsou kružnice se středem v počátku, nakreslete obrázek s těmito vrstevnicemi a vyznačte do tohoto obrázku gradienty v bodech \(\displaystyle A=(0,1)\), \(\displaystyle B=(1,0)\) a \(\displaystyle C=(1,1)\)

Uvažujte součinitel tepelné vodivosti

\[\begin{split}\lambda =\begin{pmatrix} 2&0\\0&3 \end{pmatrix}\end{split}\]

a vypočtěte tok tepla v bodech \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\). Porovnejte směr tohoto toku se směrem gradientu a vysvětlete svá pozorování. Snaží se matice usměrnit teplo do směru osy \(\displaystyle x\) nebo do směru osy \(\displaystyle y\)? Odpovídá situace spíše dřevu s podélným směrem v ose \(\displaystyle x\) nebo v ose \(\displaystyle y\)?

Řešení

Platí

\[\pdv{T}{x}=-\frac 12 (x^2+y^2)^{-\frac 12}(2x)=-\frac{x}{\sqrt{x^2+y^2}}\]

a ze symetrie

\[\pdv{T}{y}=-\frac{y}{\sqrt{x^2+y^2}}.\]

Odsud

\[\nabla T=\qty(-\frac{x}{\sqrt{x^2+y^2}},-\frac{y}{\sqrt{x^2+y^2}})^T=-\frac 1{\sqrt{x^2+y^2}}(x,y)^T.\]

Tok tepla je

\[\begin{split}\vec q=-\lambda \nabla T=\frac 1{\sqrt{x^2+y^2}}\begin{pmatrix} 2&0\\0&3 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}=\frac 1{\sqrt{x^2+y^2}} \begin{pmatrix} 2x\\3y \end{pmatrix} \end{split}\]

Dosazením dostáváme \(\displaystyle \vec q(A)=(0,3)^T\), \(\displaystyle \vec q(B)=(2,0)^T\), \(\displaystyle \vec q(C)=\frac 1{\sqrt{2}}(2,3)^T\). Porovnáním s gradientem \(\displaystyle \nabla T(A)=-(0,1)^T\), \(\displaystyle \nabla T(B)=-(1,0)^T\) a \(\displaystyle \nabla T(C)=-\frac 1{\sqrt 2}(1,1)^T\) vidíme, že v bodech \(\displaystyle A\) a \(\displaystyle B\) je tok proti směru gradientu, v bodě \(\displaystyle C\) se tok stáčí do směru osy \(\displaystyle y\). Protože v ose \(\displaystyle y\) má dřevo větší vodivost, jedná se o podélný směr. To je ale vlastně vidět už ze zadané matice.

Testová otázka Testová otázka Testová otázka

2.8. Gradient numericky

Video

\(\displaystyle T\)	\(\displaystyle -30\)	\(\displaystyle -25\)	\(\displaystyle -20\)	\(\displaystyle -15\)	\(\displaystyle -10\)	\(\displaystyle -5\)	\(\displaystyle 0\)	\(\displaystyle 5\)	\(\displaystyle 10\)	\(\displaystyle 15\)	\(\displaystyle 20\)	\(\displaystyle 25\)	\(\displaystyle 30\)
\(\displaystyle -30\)	81.39	84.14	86.39	88.14	89.39	90.14	90.39	90.14	89.39	88.14	86.39	84.14	81.39
\(\displaystyle -25\)	83.47	86.22	88.47	90.22	91.47	92.22	92.47	92.22	91.47	90.22	88.47	86.22	83.47
\(\displaystyle -20\)	85.54	88.29	90.54	92.29	93.54	94.29	94.54	94.29	93.54	92.29	90.54	88.29	85.54
\(\displaystyle -15\)	87.62	90.37	92.62	94.37	95.62	96.37	96.62	96.37	95.62	94.37	92.62	90.37	87.62
\(\displaystyle -10\)	89.69	92.44	94.69	96.44	97.69	98.44	98.69	98.44	97.69	96.44	94.69	92.44	89.69
\(\displaystyle -5\)	91.77	94.52	96.77	98.52	99.77	100.52	100.77	100.52	99.77	98.52	96.77	94.52	91.77
\(\displaystyle 0\)	93.84	96.59	98.84	100.59	101.84	102.59	102.84	102.59	101.84	100.59	98.84	96.59	93.84
\(\displaystyle 5\)	95.92	98.67	100.92	102.67	103.92	104.67	104.92	104.67	103.92	102.67	100.92	98.67	95.92
\(\displaystyle 10\)	97.99	100.74	102.99	104.74	105.99	106.74	106.99	106.74	105.99	104.74	102.99	100.74	97.99
\(\displaystyle 15\)	100.07	102.82	105.07	106.82	108.07	108.82	109.07	108.82	108.07	106.82	105.07	102.82	100.07
\(\displaystyle 20\)	102.14	104.89	107.14	108.89	110.14	110.89	111.14	110.89	110.14	108.89	107.14	104.89	102.14
\(\displaystyle 25\)	104.22	106.97	109.22	110.97	112.22	112.97	113.22	112.97	112.22	110.97	109.22	106.97	104.22
\(\displaystyle 30\)	106.29	109.04	111.29	113.04	114.29	115.04	115.29	115.04	114.29	113.04	111.29	109.04	106.29

Tabulka \(\displaystyle T(x,y)\), vodorovně \(\displaystyle x\), svisle \(\displaystyle y\)

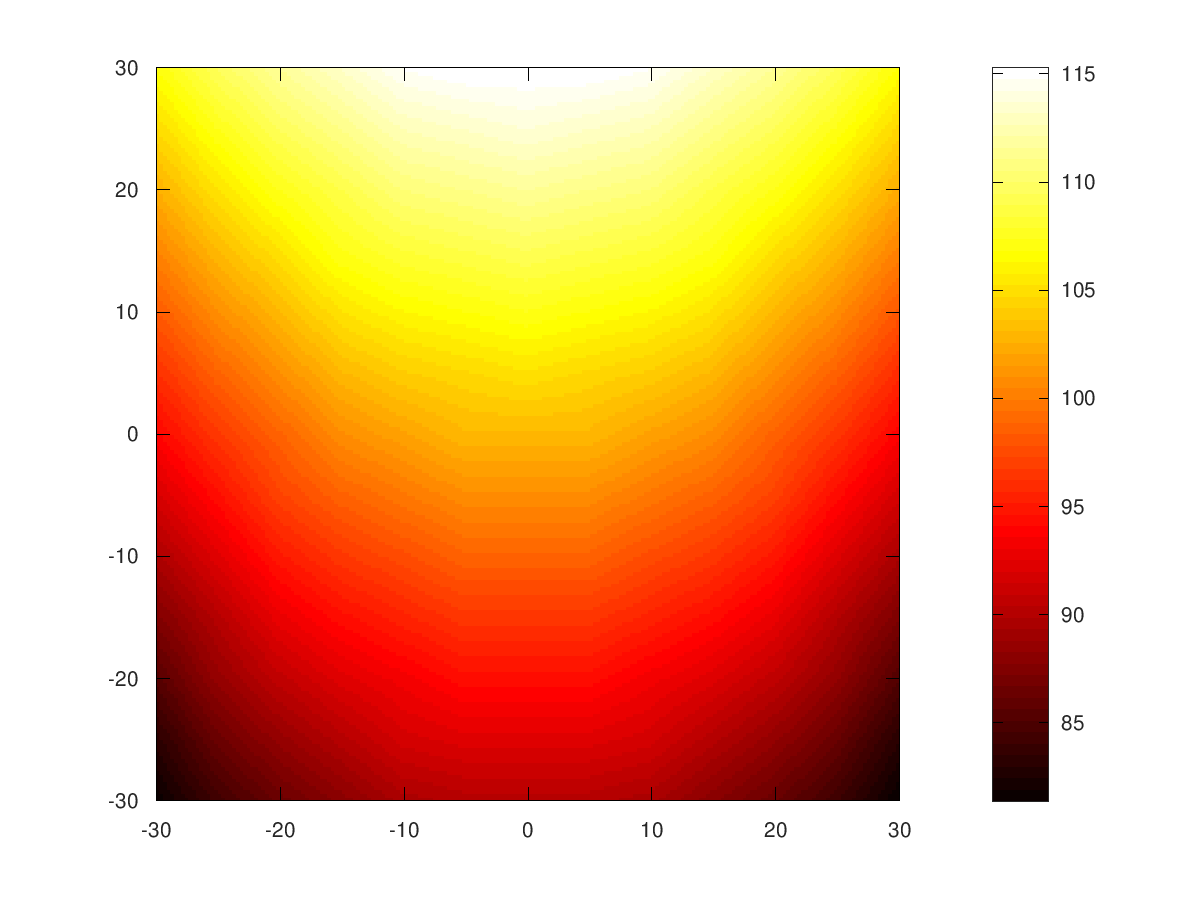
Obr. 2.17 „Termosnímek“ k tabulce. Pozor na to, že v tabulce rostou hodnoty \(\displaystyle y\) směrem dolů, ale v grafu nahoru.

Rozložení teploty v plošném materiálu je po vyhodnocení dat z termosnímku dáno tabulkou. Situace může vypadat například jako v tomto zadání. Určete gradient teploty v bodě o souřadnicích \(\displaystyle x=20\) a \(\displaystyle y=5\). Pro výpočet parciálních derivací použijte centrální diferenci.

Poznámka: Ve skutečnosti se nejedná a termosnímek, ale o graf funkce dané tabulkou. Barvy jsou interpolovány pro hladší přechody. Příkazy generující tabulku a obrázek jsou zde.

Řešení

Pomocí centrální diference odhadneme parciální derivace pro \(\displaystyle x=20\) a \(\displaystyle y=5\).

\[\frac{\partial T}{\partial x}\approx \frac{98.67-102.67}{2\times 5}=-0.4\]

\[\frac{\partial T}{\partial y}\approx \frac{102.99-98.84}{2\times 5}=0.415\]

Gradient je

\[\begin{split}\nabla T=\begin{pmatrix} -0.400\\ 0.415\end{pmatrix}.\end{split}\]

Směřuje tedy doleva nahoru. To koresponduje s obrázkem, v bodě \(\displaystyle x=20\) a \(\displaystyle y=5\) teplota roste směrem doleva a nahoru.

Testová otázka