Matematické animace
Maticový součin jako transformace roviny
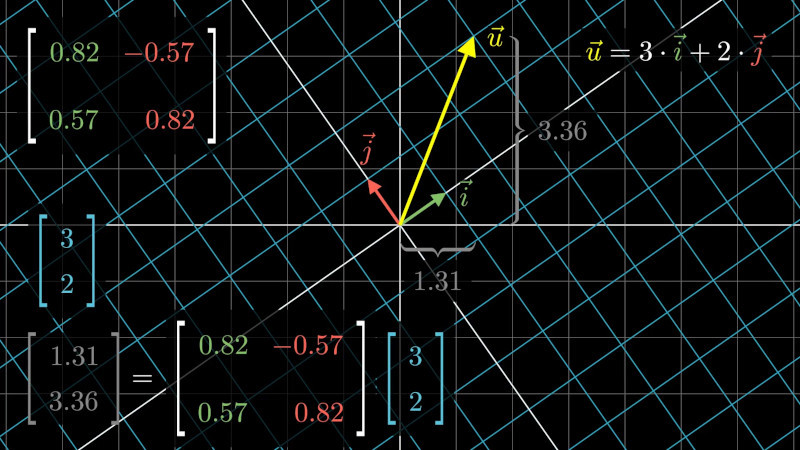
Správné pochopení maticového součinu je důležité pro pochopení, jak formulujeme materiálové vztahy pro anizotropní materiály. Nejde přitom o pochopení ve smyslu "umět vynásobit", ale o získání přehledu, jaký vyjadřovací jazyk dostáváme v maticovém součinu k dispozici a k čemu všemu je možné maticový součin využít. Zatím není video, jenom prezentace pro promítání na přednášce.
lineární algebra, součin matic, transformace souřadnic
Transformace tenzoru malých deformací
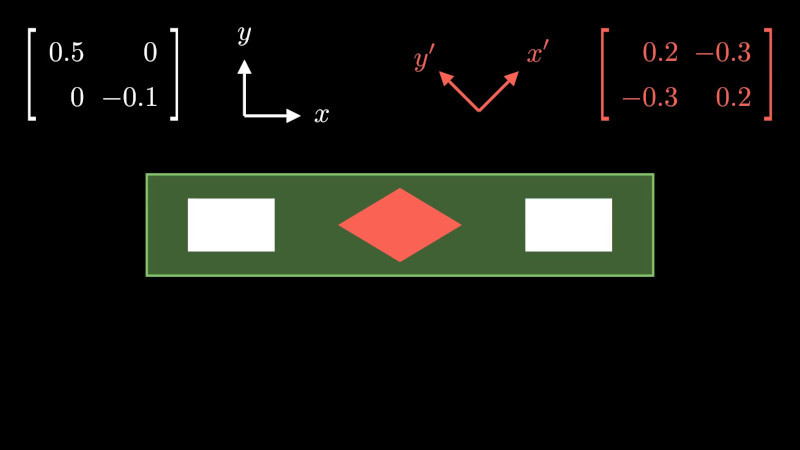
Prezentace ukazuje, že tenzor malých deformací má v různých soustavách různé komponenty. Ukazuje využití symetrie jako argumentu pro zdůvodnění hodnot některých komponent tenzoru deformace. Ukazuje, jak transformovat tenzor deformace do soustavy s otočenými osami jenom s využitím lineární algebry (bez Mohrovy kružnice a bez vzorců se směrovými kosiny).
lineární algebra, součin matic, transformace tenzoru
Anatomické směry dřeva a vlastní směry matice
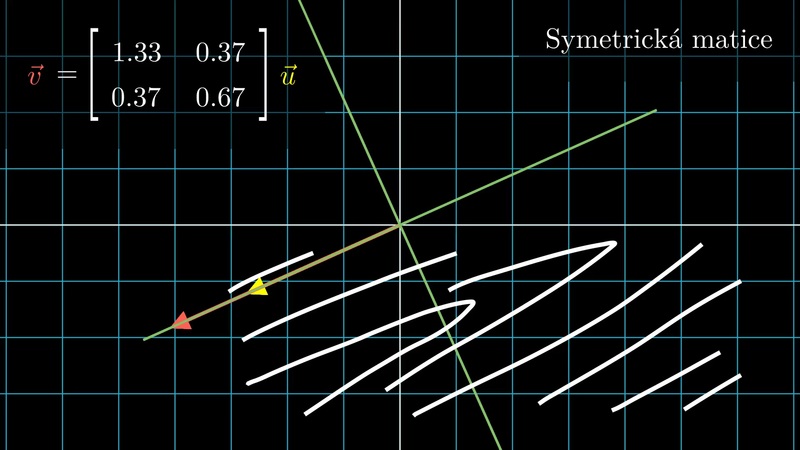
Prezentace podává geometrickou interpretaci vlastních směrů matice. Dále je ukazána souvislost vlastních směrů matice s charakteristickými směry v materiálu. Konkrétně ve dřevě.
lineární algebra, součin matic, vlastní směry a vlastní hodnoty
Rovnice vedení tepla v jedné dimenzi
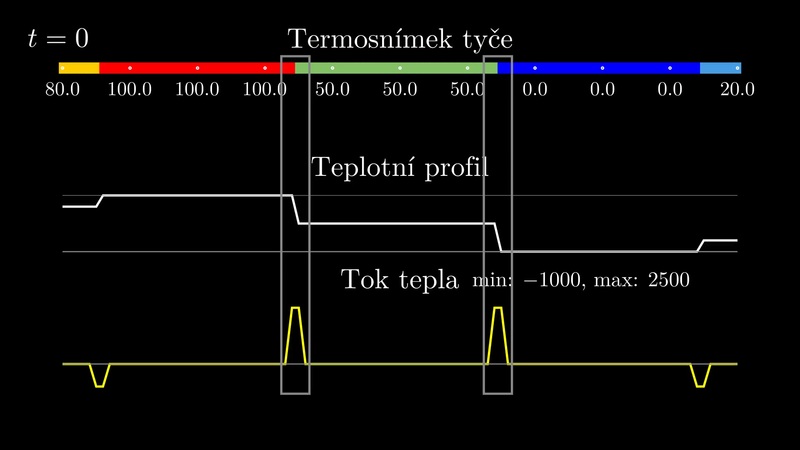
Ve videu je ukázáno, jak probíhá vedení tepla v jedné dimenzi (podél tyče, napříč stěnou apod.) a jak umíme principy řídící tento proces modelovat pomocí matematických vztahů.
diferenciální rovnice, parciální derivace, rovnice mateamtické fyziky
Gradient a tok ve dřevě a ortotropních materiálech
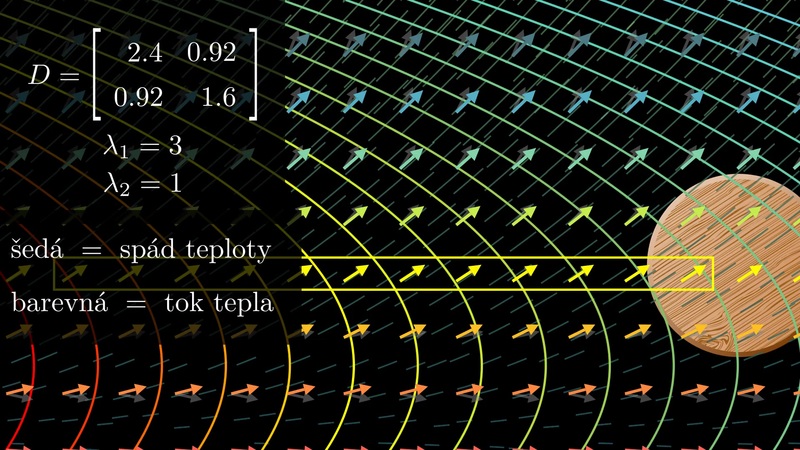
Prezentace ukazuje, jak se spád teploty projeví na toku tepla. Je uvažován dvoudimenzionální případ a materiál s odlišnými vlastnostmi v odlišných směrech. Typickým materiálem tohoto typu je dřevo. Znakem takových materiálů je, že materiálové charakteristiky nejsou konstanty, ale tenzory druhého řádu (matice).
lineární algebra, parciální derivace, gradient, součin matic
Konečné diference a simulace Newtonova zákona ochlazování

Ve videu jsou shrnuty metody umožňující popisovat rychlost růstu funkce, ať již spojité či definované pouze na izolovaných bodech. Ukázkou využití je numerická simulace Newtonova zákona ochlazování. Pro fyzikální vyjádření tohoto zákona je přirozené použít okamžitou rychlost změny teploty, tedy je přirozené pracovat se spojitou funkcí a derivací. Pro numerickou simulaci je nutné derivaci nahradit sledováním změn na izolovaných bodech, tedy místo derivace použijeme konečné diference.
diferenciální rovnice, derivace, konečná diference
Divergence a rovnice kontinuity

Ve videu je ukázáno, jak probíhá vedení tepla v jedné dimenzi (podél tyče, napříč stěnou apod.) a jak umíme principy řídící tento proces modelovat pomocí matematických vztahů.
parciální derivace, divergence, rovnice kontiuity, rovnice matematické fyziky
Logistický lov
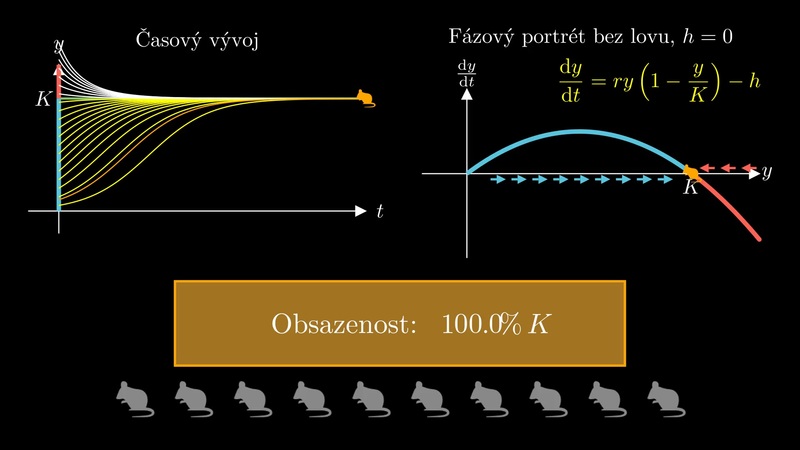
Prezentace se zabývá logistickou diferenciální rovnicí. Ukazuje, že tato rovnice je přirozeným matematickým modelem popisujícím populaci vyvíjející se v prostředí s omezenou nosnou kapacitou a vystavenou lovu. Dále je ukázáno, jak z pravé strany diferenciální rovnice poznáme stacionární body a jejich stabilitu.
diferenciální rovnice, derivace, stabilita stacionárních bodů, populační modely
Model dravce a kořisti
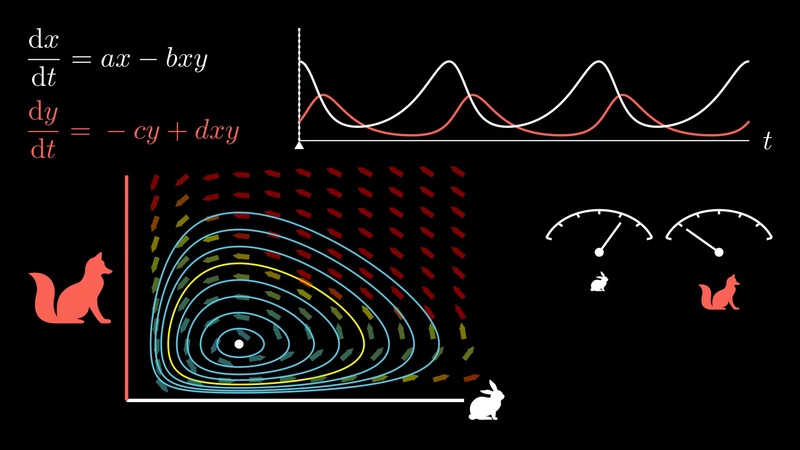
Klasický Lotkův Volterrův model dravce a kořisti. Odvození rovnic, několik způsobů vizualizace a diskuse, jak parametry ovlivňují chování řešení.
diferenciální rovnice, autonomní systémy, derivace
Stacionární body diferenciální rovnice a jejich bifurkace
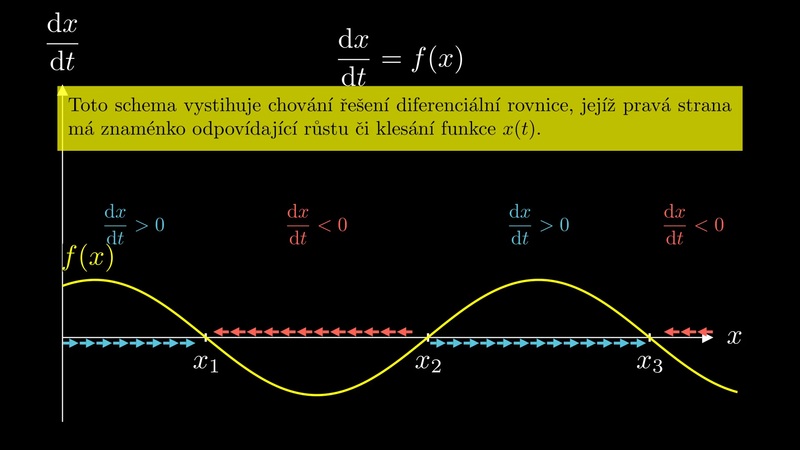
Diferenciální rovnice jsou základním vyjadřovacím prostředkem pro většinu matematických modelů dějů a jevů v přírodě nebo v technických aplikacích. Podstatnou informací jsou informace o počtu stacionárních bodů a jejich stabilitě. Jak tuto informaci zjistit s minimální námahou a jak identifikovat situace, kdy se počet stacionárních bodů může změnit malou změnou podmínek, je shrnuto v prezentaci.
diferenciální rovnice, bifurkace, stacionární body
Model populace obaleče

Diferenciální rovnice je možno použít pro vysvětlení, proč v kanadských lesích dochází k periodickému přemnožování obaleče Choristoneura fumiferana. Ukazuje toto přemnožování jako nevyhnutelný důsledek růstu lesa a omezené kapacity predátorů, kteří konzumují potravu jenom do svého nasycení.
diferenciální rovnice, bifurkace, logistický růst, populační modely
Model soupeření jestřábí a holubičí povahy
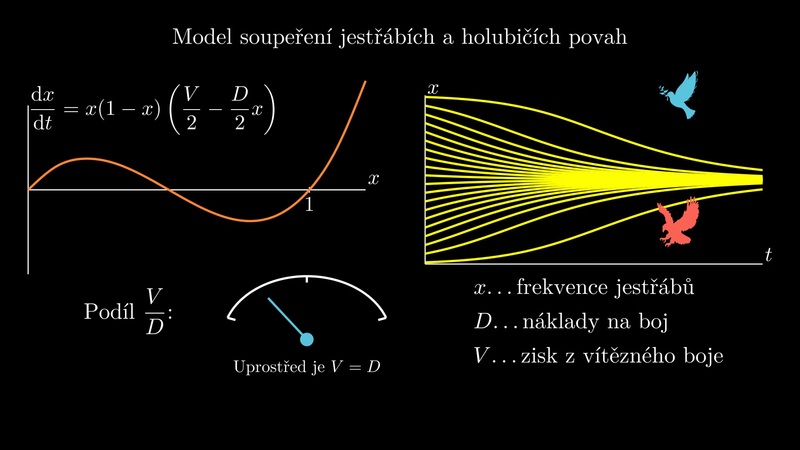
Diferenciální rovnice je možno použít pro vysvětlení, proč je populace, kde mezi sebou jedinci nebojují, ekologicky nestabilní a neudržitelná.
diferenciální rovnice, bifurkace
Zákon šíření chyb
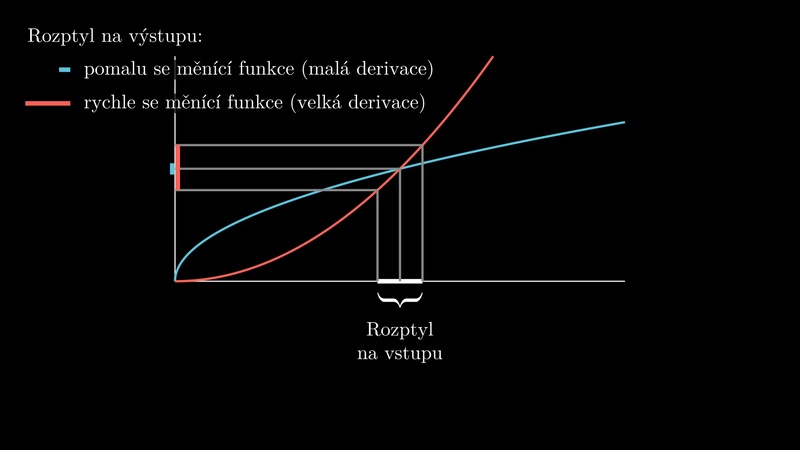
Zákon šíření chyb udává, jak se nepřesnosti ve stanovení naměřených veličin projeví na nepřesnosti, se kterou je stanovena veličina, kterou z těchto dat vypočítáváme.
Zatím není video, jenom prezentace pro promítání na přednášce.
parciální derivace
Model konkurence dvou druhů
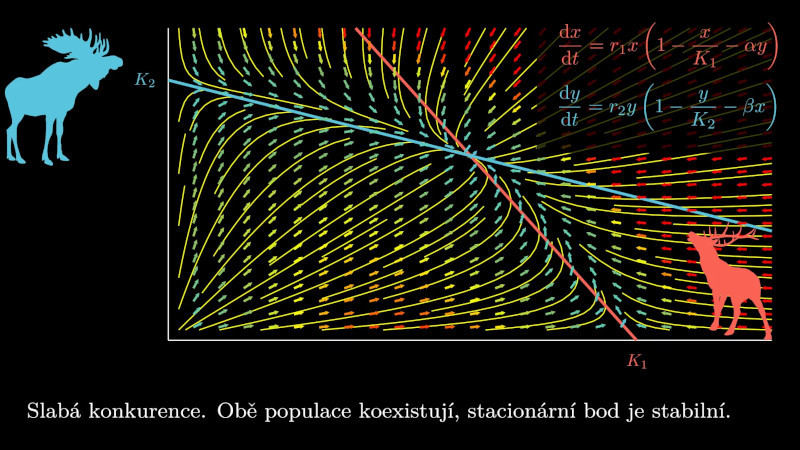
Diferenciální rovnice a jejich soustavy je možno použít pro vysvětlení různých scénářů, popisujících vývoj populace, vystavené konkurenčnímu boji s druhou populací. Existuje několik možností, jako dominance některé z populací, silná konkurence nebo slabá konkurence. Analýzou modelu je možné zjistit, kdy která z možností nastává.
Zatím není video, jenom prezentace pro promítání na přednášce.
diferenciální rovnice, populační modely
Transformace diferenciálních rovnic

Diferenciální rovnice používané k modelování reálných dějů obsahují zpravidla jisté množství parametrů. Pro numerické simulace a experimenty je vhovné počet parametrů redukovat. To je možné udělat vhodnou transformací diferenciální rovnice. Tato transformace odpovídá alternativní volbě fyzikálních jendotek a nemá vliv na chování rovnice. Ukážeme si dva přístupy. Nejprve fyzikální s postupným přizpůsobováním jednotek tak, aby model byl co nejjednodušší. Dále čistě formální a ryze matematický přístup založený na vztahu derivace funkce a derivace jejího násobku.
diferenciální rovnice, transformace, rovnice ochlazování, logistická rovnice
Lineární aproximace v praxi
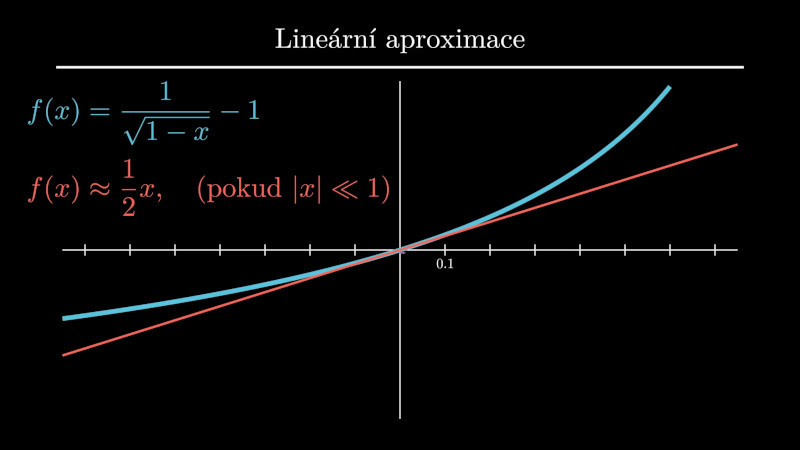
Lineární aproximace je jeden z nejmocnějších inženýrských nástrojů. Prezentace se zaměřuje na jednu konkrétní ukázku, kdy se složitý univerzálně platný vzorec pro kinetickou energii redukuje na jednoduchý středoškolský, který je sice mnohem jednodušší, ale platí jenom pro běžné rychlosti.
Vlastní čísla lineárních autonomních systémů
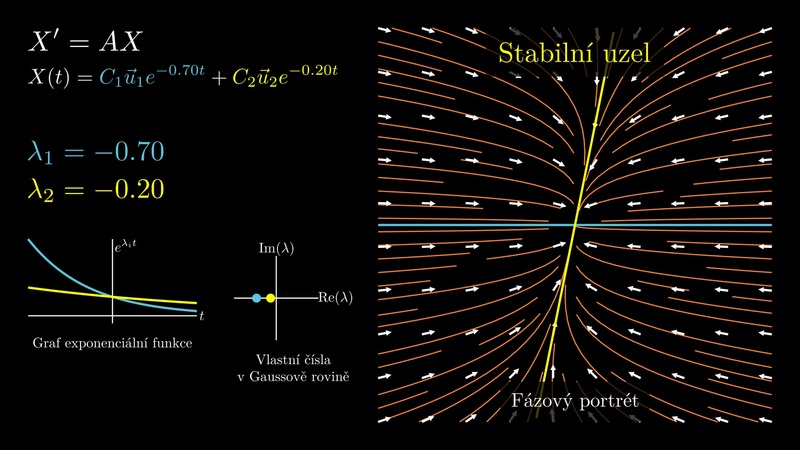
Chování trajektorií v okolí stacionárních bodů lineárního autonomního systému je možné odhalit pomocí vlastních čísel. Prezentace (video bude následovat) ukazuje, jak na to.
Linearizace autonomních systémů
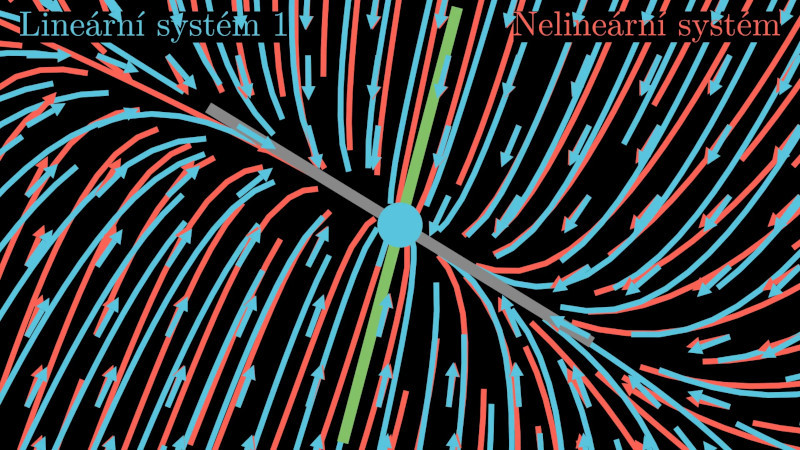
Lineární aproximace autonomních systémů umožňuje popsat chování řešení. To nás zajímá zejména u stacionárních bodů (všude jinde je to triviální a trajektorie míří směrem, kterým míří směrové pole).
Křivkový integrál druhého druhu
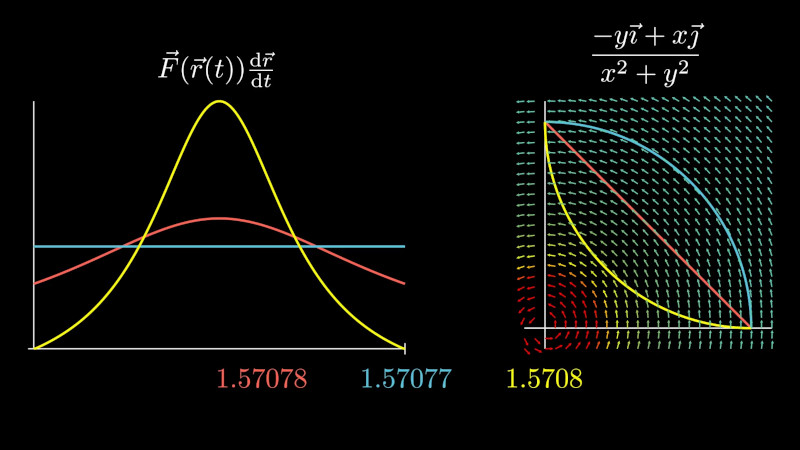
Křivkový integrál druhého druhu může a nemusí záviset na integrační cestě. Pokud nezávisí, znamená to, že v zadaném vektorovém poli je možné definovat potenciál (obdoba potenciální energie gravitačního pole) a přejít od vektorového popisu k nesrovnatelně jednoduššímu skalárnímu ppisu.
Nosník

Odvození rovnice ohybové čáry nosníku a role kvadratického momentu průřezu při deformaci.
Hlavní myšlenka pro zavedení derivace
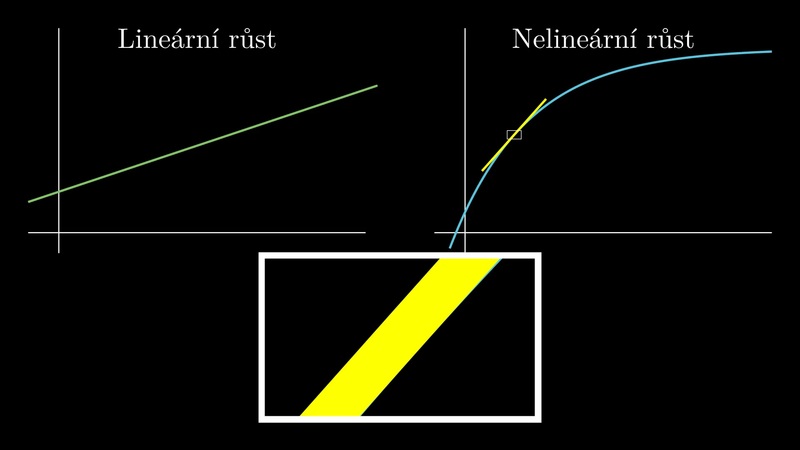
Definice derivace je založena na tom, že umíme dobře měřit rychlost růstu lineární funkce a že nelineární růst je při dostatečném zvětšení podobný lineárnímu.
Derivace a chování funkce
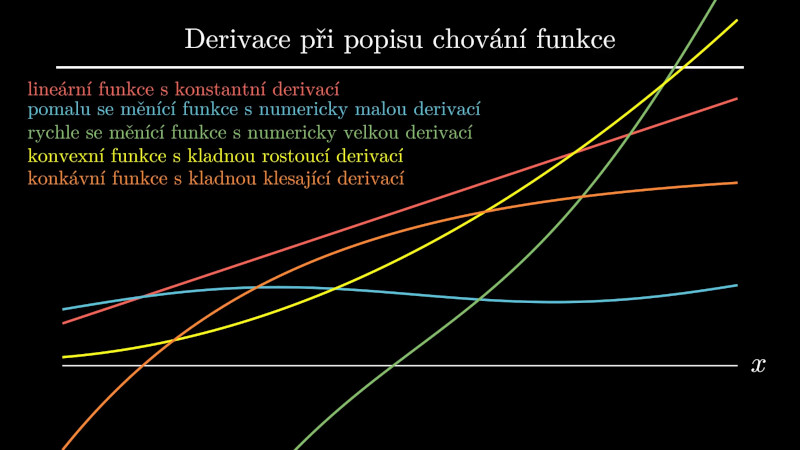
Pomocí derivace dokážeme zjistit, jak rychle funkce roste a také, jak rychle se tato rychlost mění.
Určitý integrál
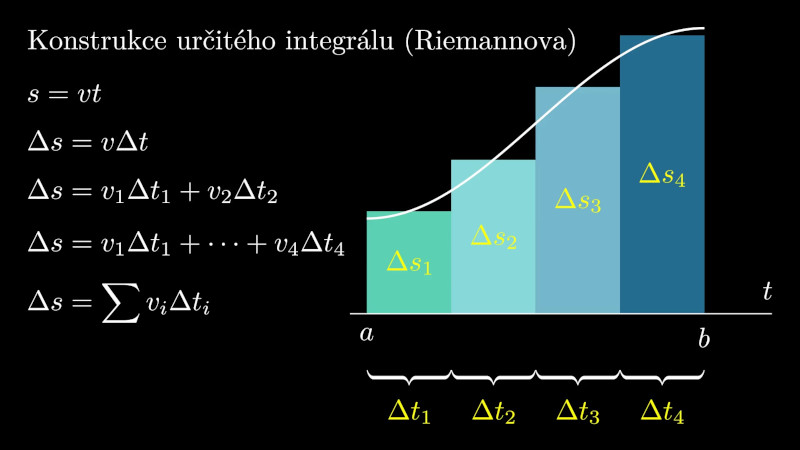
Pomocí určitého integrálu zpravidla určujeme veličiny, které jsou aditivní, které bychom v případě konstantních podmínek určili prostým součinem, ale podmínky konstantní nejsou. Klasickým příkladem je poloha pohybu, který probíhá proměnnou rychlostí.
Rotace Sarussovým pravidlem
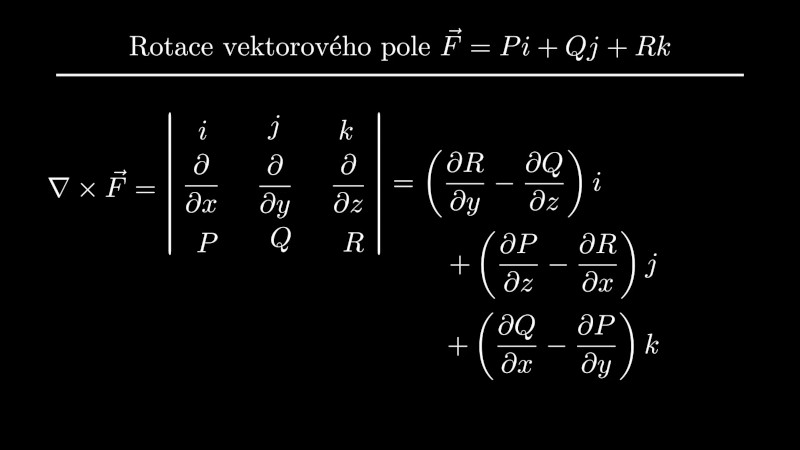
Rotace vektorového pole se počítá jako vektorový součin nabla operátoru a vektorového pole. Pro zápis je výhodné Sarussovo pravidlo výpočtu determinantů.
Směrové pole
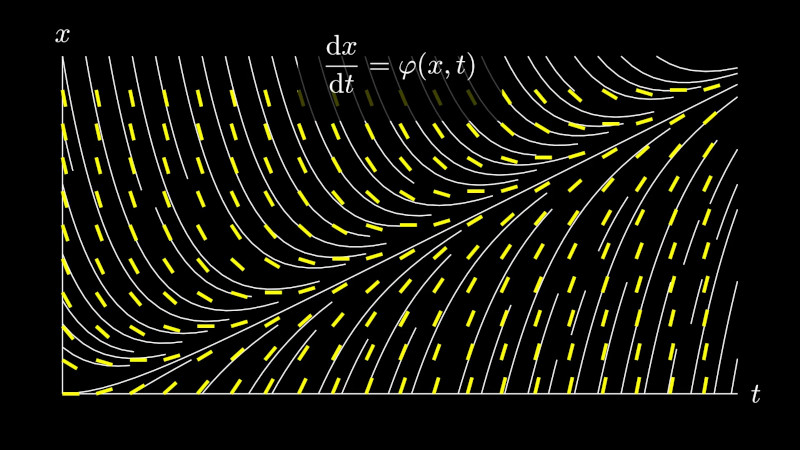
Animace tvorby směrového pole a kreslení integrálních křivek do směrového pole.
Spojitost, limita
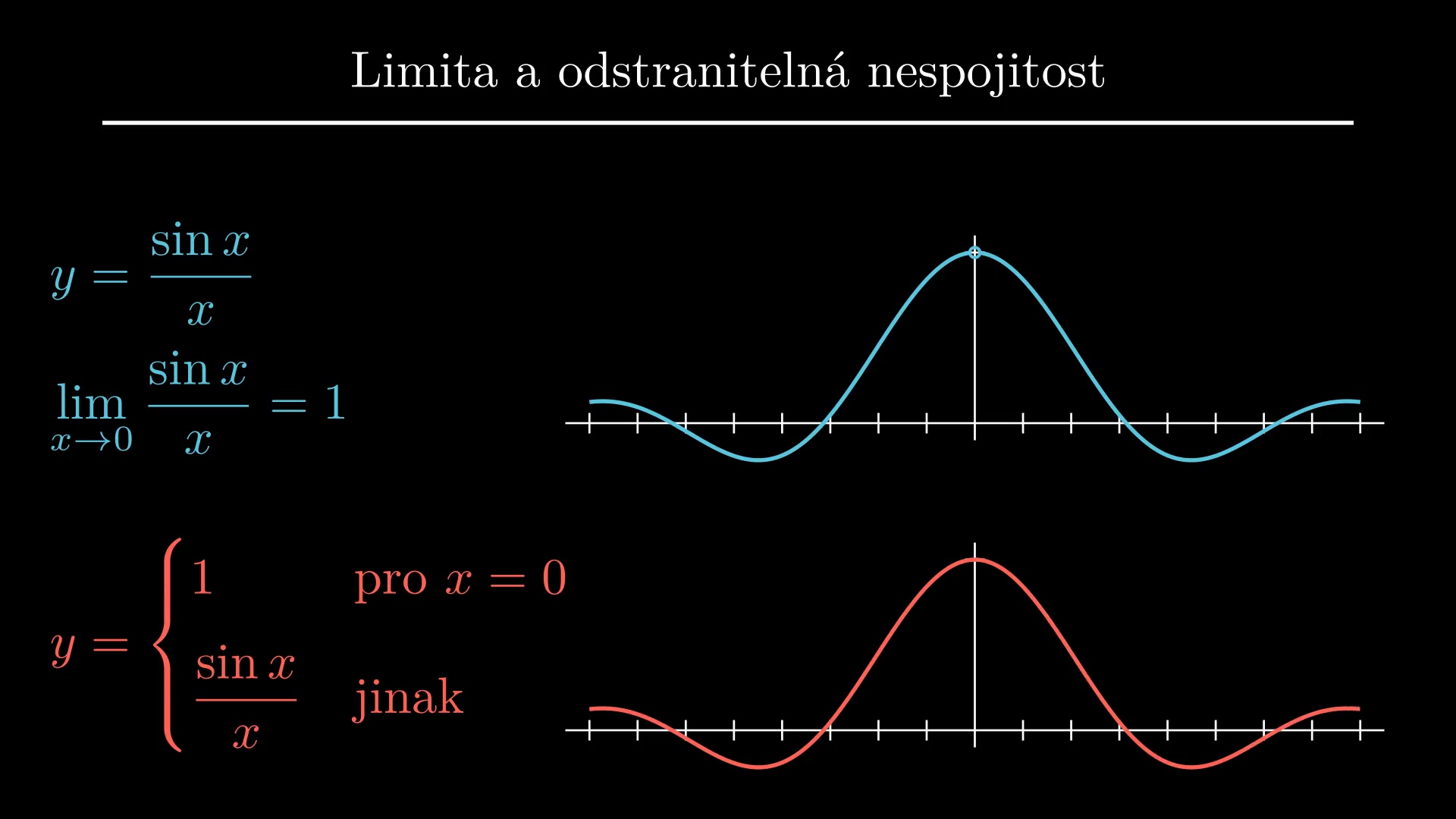
Limita pro nás bude pomocný nástroj, který umožňuje v některých případech dodefinovat nespojité funkce tak, aby se staly spojitými. V určitém smyslu nám tam umožní v některých případech dělat dosud zakázané operace, jako napříkald dělení nulou.