Derivace (snad) přirozenou cestou

V tomto článku se pokusím podat přirozenou cestu k derivaci a jejímu praktickému významu.

Role derivace při popisu světa je neocenitelná. Derivace je přirozeným jazykem, pokud se snažíme popsat základní principy, podle kterých funguje příroda, a pokud se snažíme najít pozorovatelné důsledky těchto principů.

Málo věcí v přírodě je statických. Většina procesů v přírodě probíhá tak, že jsou iniciovány nějakou nerovnováhou a příroda se snaží rovnováhu obnovit. Proto fouká vítr z oblastí s větším tlakem do oblastí s menším tlakem. Proto se studenému nápoji předává teplo z okolí a teploty se vyrovnávají.

Je přirozené, že intenzita procesu obnovujícího rovnováhu souvisí s tím, jak moc je nerovnováha velká. Mezi oblastmi s obrovským rozdílem tlaků fouká silný vítr. Na sluneční výhni se studený nápoj ohřívá rychleji než ve stínu. Rychlost je skryta v naprosté většině přírodních dějů. Pokud se o rychlost začneme zajímat a chceme s ní umět pracovat, jsme na cestě dojít k definici derivace.

Motivace na úvod

Schopnost pracovat s tím, čemu dnes říkáme derivace, katapultovala Isaaca Newtona mezi nejslavnější vědce všech dob. Obrázek z https://cs.wikipedia.org/wiki/Isaac_Newton

Že je při popisu přírody nutné používat nástroj, jaký dnes známe jako derivaci, začínalo být vědcům jasné na začátku 17. století. Protože se jednalo o zcela nový přístup, nebylo hledání nové cesty jednoduché. Na problematice pracovala řada prominentních vědců tehdejší doby (Fermat, Kopernik, Cavalieri). Na konci 17. století učinil rozhodující krok anglický fyzik Isaac Newton. Díky tomu, že Newton ovládl práci s derivacemi, získal tak obrovský náskok před svými konkurenty, že je dnes považován za jednoho z největších vědců v celé historii lidstva. Do doby Newtona lidé dokázali v řadě případů popsat, jak věci fungují. S Newtonovým přístupem bylo možné ukázat, proč věci fungují právě tímto způsobem. Například byly známy Keplerovy zákony pohybu planet. Vědělo se, že planety obíhají po eliptických drahách, že plošná rychlost je konstantní a že je souvislost mezi délkou polosy orbity a oběžnou dobou. Nebylo však zřejmé proč se planety pohybují podle těchto zákonů. Newtonův přístup umožňuje ukázat, že Keplerovy zákony jsou důsledkem obecných pohybových zákonů a toho, že gravitační síla klesá s druhou mocninou vzdálenosti. Jinými slovy ukázal, že zákony pohybu planet je možné odvodit z obecnějších fyzikálních principů. Aby to ukázal, musel použít zcela nový matematický aparát, který odpovídá dnešním derivacím. Nazýváme jej diferenciální počet.

Diferenciální počet způsobil revoluci v možnostech popisu přírody. Neměl však ihned dnešní podobu. Teorie měla řadu slabých míst, která bylo nutno překonávat víceméně intuitivně a proto si tento přístup našel i řadu kritiků. Do podoby ucelené matematické teorie diferenciální počet dotáhli až v 19. století Cauchy, Riemann a Weierstrass. Nezávisle na Newtonovi a přibližně ve stejnou dobu objevil diferenciální počet i francouzský učenec Wilhelm Leibniz.

Stručně shrnuto: derivace a s nimi související nástroje jsou velmi silný nástroj umožňující modelovat přírodní děje od základních principů k pozorovatelným datům. Není to však triviální matematický koncept. I největším vědcům historie trvalo dlouhá desetiletí, než našli vhodný postup, jak s derivacemi pracovat.

Vzhledem k uvedenému si ukážeme zejména hlavní myšlenku a koncepčně obtížnější věci (limita a spojitost) jenom stručně okomentujeme.

Rychlost přirozenou logikou

Podle nepodložené historky Newtona k jeho teorii inspirovalo jablko, které mu spadlo na hlavu. Stejně tak jej mohla inspirovat tepelná výměna mezi kávou a okolním vzduchem. Obrázek: Generovaný AI.

Uvažujme následující situaci. Teplota studeného nápoje v teplé místnosti roste. Za 10 minut se teplota zvýší ze čtyř stupňů Celsia na deset. Naroste tedy o šest stupňů Celsia za 10 minut. Pro posouzení rychlosti ohřevu je přirozené tento přírůstek vztáhnout k nějakému referenčnímu času, nejlépe k jednotce času, tedy k minutě. Pokud navýšení šest stupňů Celsia rozdělíme rovnoměrně na celý časový úsek deseti minut, připadá na každou minutu navýšení o šest desetin stupně Celsia. To snadno zjistíme dělením.

Rychlost růstu teploty je šest desetin stupně Celsia za minutu. Tato informace je nesmírně zajímavá. V čem ja zajímavá a co z ní můžeme zjistit?

• Je získaná z jednoduchých dat. Výchozí informací byly dvě teploty a časový interval. To je malé množství informací. Výpočet se tedy dá provést i s málem informací.
• Je získaná jednoduchými matematickými operacemi. Byla použita jedna operace rozdílu a jedno dělení. Není potřeba žádná specifická činnost, která by znemožnila výpočet automatizovat.
• Výpočet dává představu, jak rychle děj probíhal. Každou minutu se teplota zvýšila o šest desetin stupně.

• Výsledek dává nástroj jak odhadnout, co se bude dít dále. Pokud teplota poroste stále stejnou rychlostí, potom například v následujících čtyřech minutách teplota vzroste o dva stupně Celsia a čtyři desetiny.

  \[0.6^\circ \mathrm C/\mathrm{min} \times 4\,\mathrm {min} = 2.4 ^\circ\mathrm C\tag{2}\]

  Výslednou teplotu určíme jako součet teploty a odhadovaného přírůstku. Za další čtyři minuty tedy teplota bude dvanáct stupňů Celsia.

  \[10^\circ \mathrm C + 0.6^\circ \mathrm C/\mathrm{min} \times 4\,\mathrm {min} = 10 ^\circ\mathrm C+2.4 ^\circ\mathrm C=12.4 ^\circ\mathrm C\tag{3}\]

Nedostatky jednoduchého přístupu

Výše uvedené úvahy jsou získány přirozeným uvažováním a nesou užitečné informace. Přesto vykazují některé nedostatky. Zejména jde o to, že proces tepelné výměny neprobíhá konstantní rychlostí. Je intenzivnější, když je teplotní rozdíl velký. To znamená, že za začátku probíhá tepelná výměna rychleji a proces se zpomaluje. Výpočet rychlosti je zprůměrováním děje na intervalu délky deset minut, jedná se o průměrnou rychlost. Pro přesnější popis děje bychom potřebovali okamžitou rychlost.

Jako analogii si můžeme představit měření rychlosti auta metrem a časomírou. Metr a časomíra jsou jednoduché nástroje (velmi jednoduchá časomíra je například kyvadlo), ale získáme pomocí nich jenom průměrnou rychlost. Okamžitou rychlost měříme specializovaným přístrojem, tachometrem.

Vylepšení jednoduchého přístupu

Hledání cesty umožňující přechod od průměrné rychlosti k rychlosti okamžité nebylo v historii vůbec snadné a ani přímočaré. Vyžadovalo to na tehdejší dobu použití převratných myšlenek, vytvoření nového matematického aparátu a jeho obhájení před vědeckou veřejností. To trvalo více než sto let naplněných náročnou prací největších mozků tehdejší doby. Přes to všechno, hlavní linie cesty k derivaci je přímým rozšířením našeho jednoduchého přístupu. Tento přístup stačí doplnit, opravit, vylepšit. To provedeme ve dvou krocích.

• Prvním vylepšením je naučit se počítat průměrnou rychlost pro intervaly libovolné (kladné) délky.
• Druhým vylepšením je najít nějaké rozumné rozšíření, které by nám umožnilo pracovat i s intervaly nekonečně malými, s intervaly prakticky nulové délky.

Průměrná rychlost na obecném intervalu

Je jisté, že budeme potřebovat detailnější informace o průběhu děje. Už nebude stačit teplota na počátku, teplota na konci a doba děje. Musíme znát teplotu v libovolném okamžiku. Musíme mít tedy nějaké pravidlo, které každému časovému údaji přiřadí teplotu. V matematice jsou taková pravidla představována funkcemi. Na vstupu již tedy nestačí tři čísla, ale na vstupu bude funkce definovaná na jistém intervalu. Naše funkce (nazvěme ji třeba $T$) bude mít nezávislou proměnnou čas a bude udávat teplotu v daném čase. Tedy $T(0)$ bude teplota na začátku, $T(10)$ bude teplota po deseti minutách a $T(t)$ bude teplota v čase $t$. Rovnice (1) má poté tvar

a je snadné ji zobecnit tak, aby počáteční čas byl $t$ a délka intervalu $h$. Průměrná rychlost v okamžiku začínajícím v čase $t$ a trvajícím po dobu $h$ je

Tím je splněn první bod, umíme počítat průměrnou rychlost na intervalu libovolné délky.

Od průměrné k okamžité rychlosti

Největším problémem bylo, že v aplikacích bychom místo průměrné rychlosti potřebovali rychlost okamžitou. Teoreticky by stačilo vzít stejný počáteční i koncový bod intervalu, na kterém počítáme průměr. Tedy použít $h=0$. Je však evidentní, že v předchozím vzorci volba $h=0$ nemá smysl. Na druhou stranu je však evidentní i to, že nějaká okamžitá rychlost fyzikálně smysl má. Aby matematici vyřešili tuto nesnáz, došli postupně k pojmu limita funkce. Můžeme si představit, že vypočítat limitu funkce v bodě znamená buď najít funkční hodnotu (pokud tato existuje), nebo její nejlepší rozumnou náhradu, pokud funkční hodnota neexistuje, ale existuje nějaká její rozumná náhrada. V jakém smyslu je zde použito slovo “rozumná náhrada” je nad rámec tohoto textu, ale v podstatě to znamená, že pokud je možné funkci spojitě rozšířit i do dosud nedefinovaného bodu, je limita prostředek, který toto zařídí. Stačí tedy ve vzorci (4) dosadit (ve smyslu limity) $h=0$ a tím dostáváme okamžitou rychlost, s jakou se mění teplota v čase. V matematice a v aplikacích tuto veličinu nazýváme derivace teploty podle času. Formálně zapsáno

kde na levé straně je označení derivace teploty podle času a na pravé straně definiční vztah pro tuto derivaci.

Toto je definice derivace, jak se ustálila na své cestě od intuitivního přístupu ke korektně definované matematické operaci. V ryze matematických učebnicích se setkáváme pouze s jiným pojmenováním proměnných a jiným označením derivace. Důvodem je stručnost a jistá setrvačnost ve volbě označení, kdy proměnná je typicky $x$, funkce je typicky $f(x)$, derivace je značena co nejúsporněji, v tomto případě čárkou za jménem funkce. Nejčastější tvar definice derivace v matematických učebnicích je potom

Využití derivací v matematických modelech

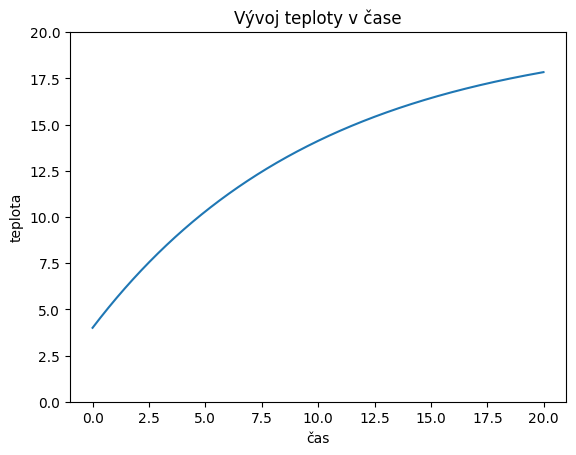
Řešením modelu (7) je následující křivka. Ukazuje, že jak teplota roste a rychlost r;stu klesá. To proto, že s růstem teploty klesá rozdíl mezi teplotou a teplotou okolí.

S derivací často pracujeme i když derivovanou funkci neznáme. Není to paradox, ale naprosto běžný přístup k formulaci fyzikálních zákonů a jejich matematických modelů. Objasníme si jej v následujícím textu.

Jak bylo řečeno v úvodu, fyzikální děje probíhají určitou rychlostí. Matematický popis této rychlosti je derivace. Například tepelná výměna mezi sklenicí chladného nápoje a teplou místností probíhá tak, že rychlost změny teploty nápoje (změna teploty za jednotku času) je přímo úměrná teplotnímu rozdílu. Rychlost změny teploty je derivace teploty podle času, teplotní rozdíl je rozdílem teplot a úměrnost znamená, že jedna veličina je konstantním násobkem druhé. Je tedy již snadné napsat matematický model procesu ve tvaru

kde $T$ je teplota studeného nápoje, $T_0$ je teplota místnosti a $k$ je konstanta úměrnosti.

Všimněte si, že derivaci jsme při formulaci matematického modelu tepelné výměny použili i přesto, že funkci $T$ neznáme. To znamená, že ji ani nemůžeme derivovat ve smyslu výpočtu derivace podle běžných pravidel pro derivaci funkcí. Přesto tato derivace existuje, je to veličina mající srozumitelnou praktickou interpretaci a můžeme s ní pracovat. Funkce $T$ popisující teplotu je v rovnici (7) neznámá, v rovnici figuruje derivace teploty a tato derivace souvisí s aktuální teplotou prostřednictvím známého vztahu. Takový vztah se nazývá diferenciální rovnice. Podobu diferenciálních rovnic mají přirozeně všechny fyzikální a přírodní zákony, které popisují dynamiku vývoje.

Shrnutí

Děje v přírodě probíhají určitou rychlostí, která ovlivňuje dynamiku a celý průběh děje.

Na základní práci s rychlostí stačí jednoduché operace: rozdíl pro zjištění o kolik se sledovaná veličina změnila a podíl pro přepočtení této změny na jednotku času, vzdálenosti či čehokoliv jiného, co je v příslušné situaci relevantní.

Pro detailní a precizní práci s rychlostí však uvedené operace nestačí. Je potřeba mít detailnější informace o průběhu děje a nástroj, který z těchto informací najde rychlost. Tedy je nutné znát funkční předpis pro veličinu měnící se v čase a derivace podle času poté určí rychlost změny této veličiny.

Bohužel, informaci uvedenou v předchozím odstavci máme k dispozici málokdy. Častěji se stává, že víme, jak rychlost změny souvisí se stavem studovaného systému. Toto bývá vyjádřeno nějakým fyzikálním zákonem. Poté můžeme sestavit rovnici, ve které je neznámou funkce popisující vývoj systému, v rovnici figuruje rychlost a tedy derivace této neznámé funkce a tato rychlost souvisí s ostatními veličinami popisujícími stav systému. Takové rovnice jsou základními prostředky pro řešení fyzikálních úloh a při modelování dějů a procesů probíhajících v přírodě.