Markovův řetězec a sukcese lesa

Markovův řetězec je jeden z nejjednodušších modelů popisujících systém, který se může nacházet v různých stavech a mezi těmito stavy se náhodně přepíná podle předem daných pravděpodobností. Pro jeho popis je vhodný matematický aparát založený na teorii matic. Následující ukázka aplikace při studiu populací je z knihy Ekologie: jedinci, populace a společenstva autorů Begon, M. and Townsend, C.R. and Harper, J.L.

Americký vědec H. S. Horn studoval druhovou skladbu lesa a vycházel z předpokladů, že existuje konstantní pravděpodobnost, že určitý druh je nahrazen jiným druhem. Tabulka pravděpodobností je níže. Pro každý současný druh jsou v řádku pravděpodobnosti, že tento druh bude za 50 let nahrazen druhem ze záhlaví příslušného sloupce. Například pravděpodobnost toho, že na stanovišti, kde nyní roste bříza topololistá poroste za 50 let červený javor je 50% (první řádek, třetí sloupec). Pravděpodobnost toho, že na stanovišti, kde nyní roste javor za 50 let poroste bříza je nulová (třetí řádek, první sloupec). Model předpokládá, že i když se dřevina v lokalitě nevyskytuje, existuje zdroj semen a dřevina se na této lokalitě může objevit.

	Bříza topololistá	Tupela lesní	Javor červený	Buk
Bříza topololistá	0.05	0.36	0.50	0.09
Tupela lesní	0.01	0.57	0.25	0.17
Javor červený	0.00	0.14	0.55	0.31
Buk	0.00	0.01	0.03	0.96

Procentuální zastoupení jednotlivých druhů budeme charakterizovat vektorem, kde hodnoty pro stromy budou ve stejném pořadí, jako jsou stromy seřazeny v naší tabulce. Pokud například je zastoupena napůl bříza a buk, odpovídá to vektoru \(v(0) = (50,0,0,50)^T.\)

Procentuální zastoupení každého druhu se bude měnit z období na období. Například procentuální zastoupení javoru v dalším období bude dáno procentuálním zastoupením javoru v současnosti a pravděpodobností, že se na stanovišti udrží a dále procentuálním zastoupením ostatních dřevin a pravděpodobností, že tato dřevina bude nahrazena javorem. Tedy pro javor a vektor procentuálního zastoupení \(v = (v_1,v_2,v_3,v_4)^T\) to bude

\[ 0.50 v_1 + 0.25v_2 + 0.55 v_3 + 0.03 v_4 \]

Při použití maticového součinu vektoru rozložení zastoupení s maticí pravděpodobností

\[M=\begin{pmatrix} 0.05 & 0.01 & 0 & 0\cr 0.36& 0.57& 0.14&0.01\cr 0.50&0.25&0.55&0.03\cr 0.09&0.17&0.31&0.96 \end{pmatrix}\]

je zastoupení dřevin v následujícím období dáno vzorcem

\[v(k+1)=Mv(k).\]

import numpy as np
import matplotlib.pyplot as plt
M = np.matrix([0.05, 0.36, 0.50, 0.09,
              0.01, 0.57, 0.25, 0.17,
              0.0,0.14,0.55,0.31,
              0.0,0.01,0.03,0.96]).reshape(4,4).T
M

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 1
----> 1 import numpy as np
      2 import matplotlib.pyplot as plt
      3 M = np.matrix([0.05, 0.36, 0.50, 0.09,
      4               0.01, 0.57, 0.25, 0.17,
      5               0.0,0.14,0.55,0.31,
      6               0.0,0.01,0.03,0.96]).reshape(4,4).T

ModuleNotFoundError: No module named 'numpy'

Zkusíme si namodelovat 20 období, tj. tisíc let vývoje. K tomu si připravíme pole do kterého budeme ukládat data. Výchozím stavem bude rovnoměrné zastoupení všech druhů. Vývoj jednotlivých dřevin zachytíme graficky.

N = 20
X_init = [25, 25, 25, 25]

X = np.zeros((4, N))
X[:, 0] = X_init
for i in range(N - 1):
    X[:, i + 1] = M @ X[:, i]

fig, ax = plt.subplots()
t = np.array(range(N))*50
plt.plot(t,X.T)
plt.legend(["Bříza topololistá", "Tupela lesní", "Javor červený", "Buk"])
ax.set(
    title="Vývoj zastoupení jednotlivých druhů",
    ylim=(0,None),
    ylabel="Procentuální podíl", 
    xlabel="Čas/rok");

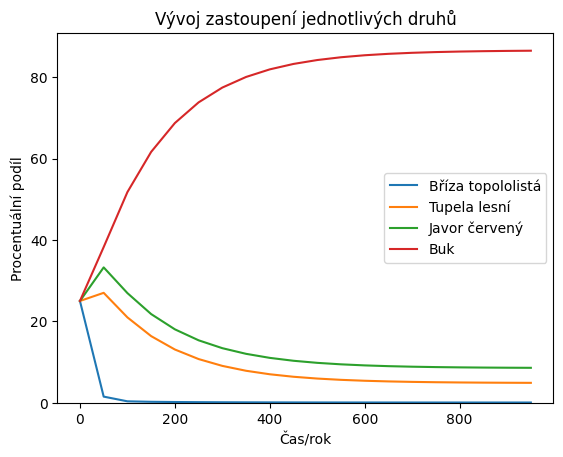
Ze simulace se zdá, že poměr dřevin se postupně stabilizuje. Z matematického hlediska se procentuální zastoupení dřevin nemění, pokud se vektor zobrazí sám na sebe. Ověříme, že to tak opravdu je.

X_final = X[:, [-1]]
print(X_final.ravel())  # array se převede na 1D pomocí ravel
print((M @ X_final).ravel())

[5.16464021e-02 4.88304501e+00 8.57619685e+00 8.64891117e+01]
[[5.14127702e-02 4.86748704e+00 8.55816607e+00 8.65229341e+01]]

Pokud bychom chtěli simulaci ne po 50 letech, ale po 100 letech, můžeme maticí vynásobit dvakrát. To je v konečném důsledku stejné, jako bychom násobili druhou mocninou. Pokud bychom chtěli delší časový interval, použijeme vyšší mocninu. Následující výpočet ukazuje, že pro dostatečně velkou mocninu vychází všechny sloupce matice stejné a jsou rovny výslednému poměru mezi jednotlivými dřevinami.

M**50

matrix([[5.08240327e-04, 5.08240330e-04, 5.08240173e-04, 5.08239864e-04],
        [4.82828193e-02, 4.82828195e-02, 4.82828090e-02, 4.82827884e-02],
        [8.51272964e-02, 8.51272966e-02, 8.51272845e-02, 8.51272607e-02],
        [8.66081644e-01, 8.66081644e-01, 8.66081666e-01, 8.66081711e-01]])

Další uplatnění Markovových řetězců je například při předpovědi počasí a jejím zpřesněním na lokální úroveň. Používá informace o tom, s jakou pravděpodobností je jeden druh počasí zachován či vystřídán druhým.