Teorie elasticity ve 3D

10. Teorie elasticity ve 3D#

10.1. Tenzor napětí#

  • Napětí je podílem velikosti působící síly a velikosti plochy, na kterou tato síla působí. Pro sílu kolmou k ploše mluvíme o normálovém napětí, pro sílu ve směru plochy o smykovém napětí.

  • Znaménková konvence - viz obrázek. Napětí v obrázku jsou kladná, opačná napětí jsou záporná. Kladné normálové napětí tedy značí tah, záporné tlak.

  • V obrázku jsou napěí pouze na třech stěnách, na zbylých šesti jsou odpovídající napětí tak, aby element byl ve statické rovnováze, tj. aby výsledná síla a výsledný moment byly nulové.

\[ \sigma = \begin{pmatrix} \sigma_x & \sigma_{xy} & \sigma_{xz}\cr \sigma_{xy} & \sigma_y & \sigma_{yz}\cr \sigma_{xz} & \sigma_{xy} & \sigma_{z} \end{pmatrix} \]

Tenzor napětí je bilineární forma, umožňuje výpočet síly na libovolně orientované ploše

10.1.1. Praktická ukázka tenzoru napětí v tříbodovém ohybu#

10.1.1.1. Tříbodový ohyb, tah v podélném směru#

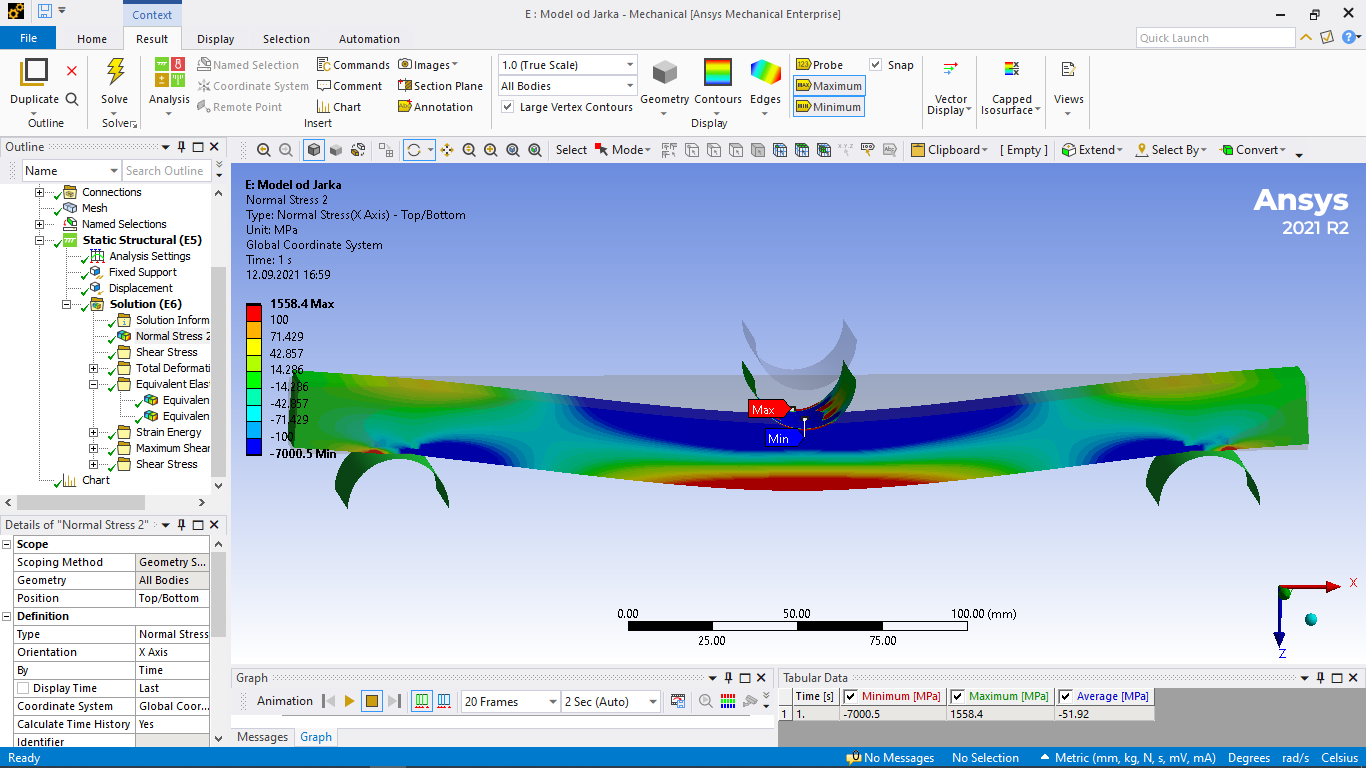
Tah na spodní straně, tlak na horní straně a před podpěrami. Zeleně neutrální oblast, kde je napětí nulové.

10.1.1.2. Tříbodový ohyb, tah v podélném směru pro čtvrtinu nosníku#

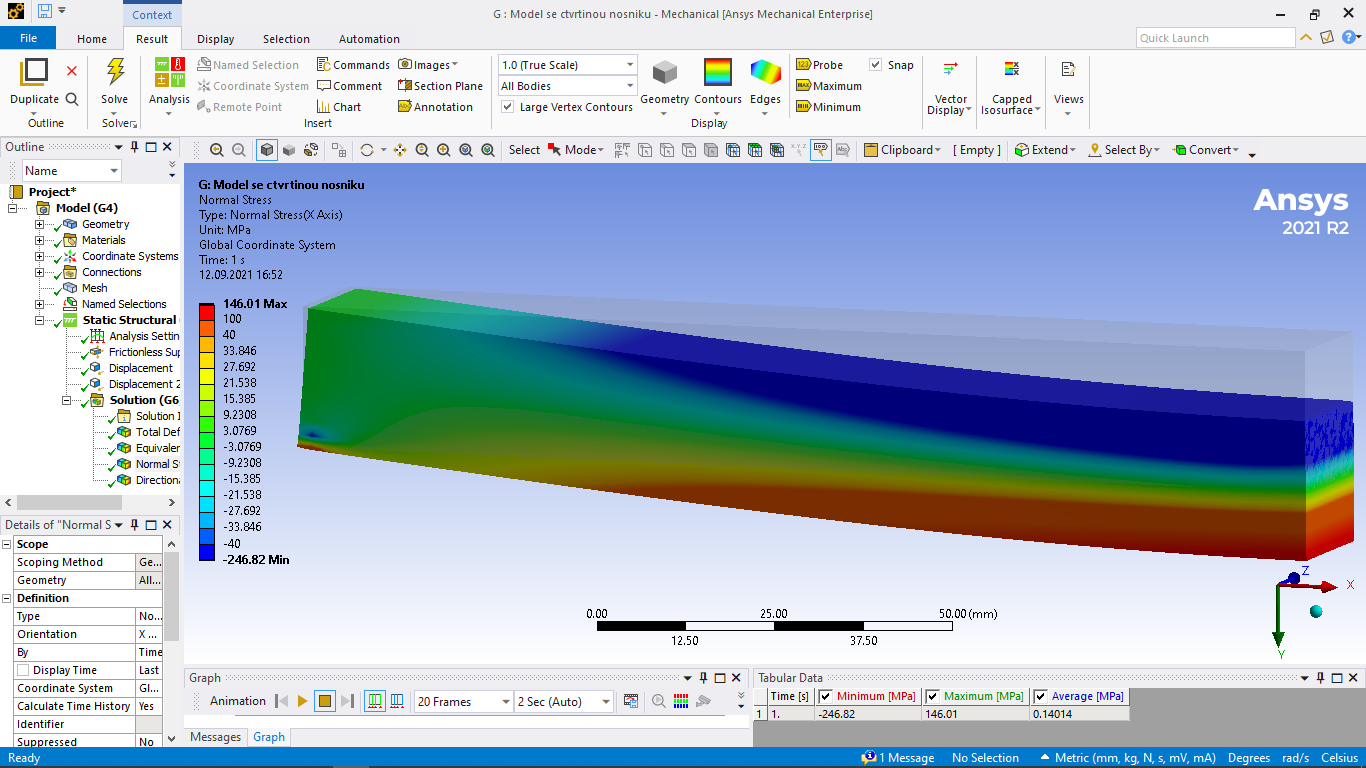
Numerická simulace pro část nosníku šetří strojový čas a nároky na paměť. V tomto případě je možné použít symetrii a počítat pouze čtvrtinu nosníku.

10.1.1.3. Tříbodový ohyb, smykové napětí#

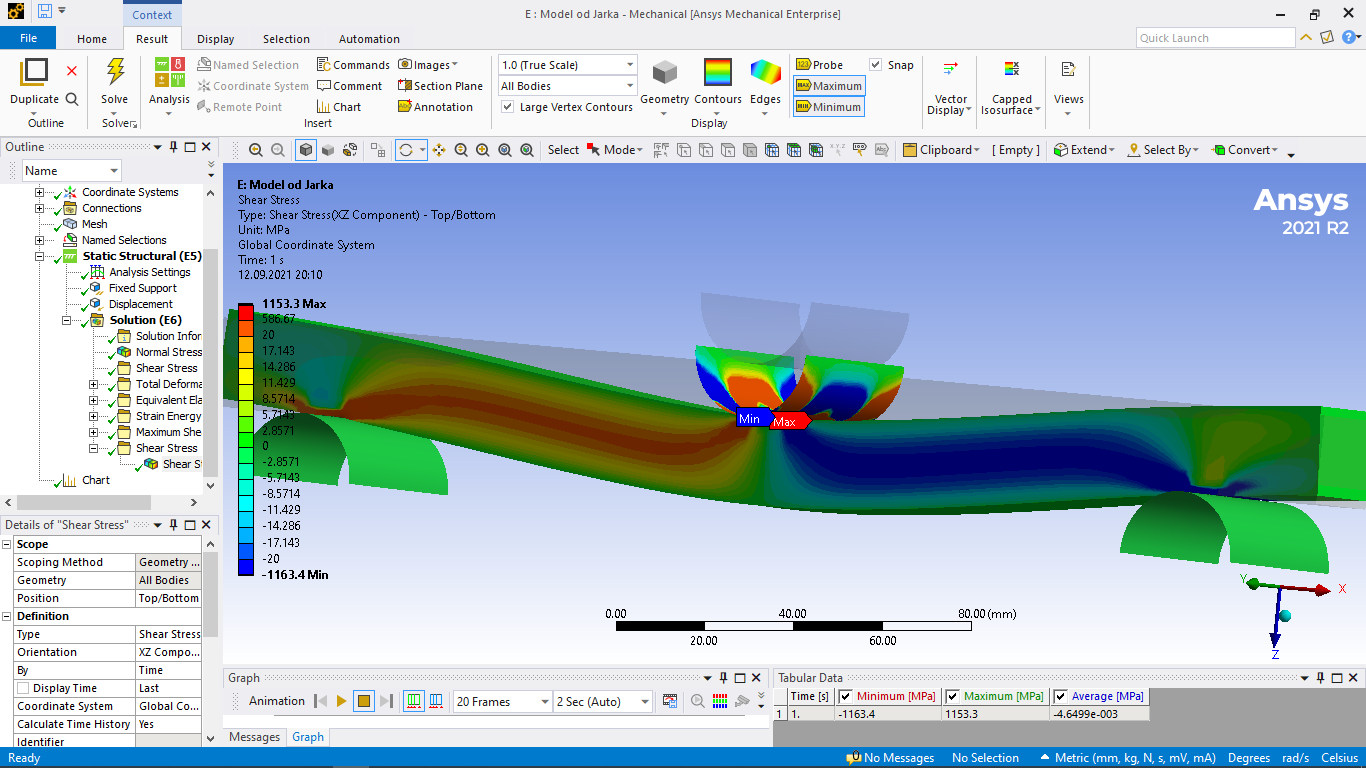
Smykové napětí v levé a pravé polovině nosníku se liší znaménkem, je antisymetrické.

10.2. Linearizace vektoru posunutí, tenzor deformace#

\[ \varepsilon = (\varepsilon_{ij}) = \left(\frac 12\left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right)\right) \]

  • Komponenty \(\varepsilon_{ii}\) jsou normálové deformace, \(\varepsilon_{ij}\) pro \(i\neq j\) jsou smykové deformace.

  • Normálová deformace udává, o kolik procent se materiál v daném směru prodlouží (kladná hodnota) nebo zkrátí (záporná hodnota). Smyková deformace udává, jak se změní pravé úhly (v obloukové míře).

10.3. Hookův zákon pro izotropní, anizotropní a ortotropní materiál#

Tenzory napětí a deformace upravíme na vektory.

\[\begin{split}\varepsilon = \left( \begin{matrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \varepsilon_{yz} \\ \varepsilon_{xz} \\ \varepsilon_{xy} \end{matrix} \right) \quad \sigma = \left( \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right) \end{split}\]

Matice poddajnosti je maticí, vyjadřující úměrnost mezi oběma tenzory.

\[\begin{split}\left( \begin{matrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \varepsilon_{yz} \\ \varepsilon_{xz} \\ \varepsilon_{xy} \end{matrix} \right) = \left( \begin{matrix} S_{11} & S_{12} & S_{13} & S_{14} & S_{15} & S_{16} \\ S_{21} & S_{22} & S_{23} & S_{24} & S_{25} & S_{26} \\ S_{31} & S_{32} & S_{33} & S_{34} & S_{35} & S_{36} \\ S_{41} & S_{42} & S_{43} & S_{44} & S_{45} & S_{46} \\ S_{51} & S_{52} & S_{53} & S_{54} & S_{55} & S_{56} \\ S_{61} & S_{62} & S_{63} & S_{64} & S_{65} & S_{66} \\ \end{matrix} \right) \left( \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right) \end{split}\]

Matice poddajnosti je symetrická

\[\begin{split}\left( \begin{matrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \varepsilon_{yz} \\ \varepsilon_{xz} \\ \varepsilon_{xy} \end{matrix} \right) = \left( \begin{matrix} S_{11} & S_{12} & S_{13} & \color{blue}S_{14} & \color{blue}S_{15} & \color{blue}S_{16} \\ & S_{22} & S_{23} & \color{blue}S_{24} & \color{blue}S_{25} & \color{blue}S_{26} \\ & & S_{33} & \color{blue}S_{34} & \color{blue}S_{35} & \color{blue}S_{36} \\ & & & S_{44} & \color{red}S_{45} & \color{red}S_{46} \\ \rlap{\text{symmetric}} & & & & S_{55} & \color{red}S_{56} \\ & & & & & S_{66} \\ \end{matrix} \right) \left( \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right) \end{split}\]

Modře vyznačené prvky dávají do relace smykové namáhání a normálové napětí. Červené vyznačené prvky dávají do relace smykové napětí v jedné rovině se smykovou deformací v jiné rovině.

10.3.1. Ortotropní materiály#

Ortotropní materiály jsou materiály, jejichž struktura se nemění při rotaci o \(180^\circ\) okolo libovolné ze tří navzájem kolmých os. Typickým představitelem je dřevo.

Při vhodné volbě souřadnic nevyvolávají normálová napětí deformaci a smyková napětí vyvolávají jenom smykovou deformaci v rovině, ve které tato napětí působí. V pravém hodním bloku matice jsou nuly a pravý dolní roh je diagonální.

\[\begin{split}\left( \begin{matrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \varepsilon_{yz} \\ \varepsilon_{xz} \\ \varepsilon_{xy} \end{matrix} \right) = \left( \begin{matrix} S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ & S_{22} & S_{23} & 0 & 0 & 0 \\ & & S_{33} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ \rlap{\text{symmetric}} & & & & S_{55} & 0 \\ & & & & & S_{66} \\ \end{matrix} \right) \left( \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right) \end{split}\]

Materiálové vlastnosti určujeme pomocí devíti na sobě nezávislých materiálových konstant. Pomocí Youngových modulů pro jednotlivé směry, pomocí Poissonova čísla a pomocí smykových modulů je možno formulovat vztah následovně.

\[\begin{split}\left( \begin{matrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \varepsilon_{yz} \\ \varepsilon_{xz} \\ \varepsilon_{xy} \end{matrix} \right) = \left( \begin{matrix} \frac 1{E_x} & -\frac{\nu_{yx}}{E_y} & -\frac{\nu_{zx}}{E_z} & 0 & 0 & 0 \\ & \frac 1{E_y} & -\frac{\nu_{zy}}{E_z} & 0 & 0 & 0 \\ & & \frac 1{E_z} & 0 & 0 & 0 \\ & & & \frac 1{G_{yz}} & 0 & 0 \\ \rlap{\text{symmetric}} & & & & \frac 1{G_{xz}} & 0 \\ & & & & & \frac 1{G_{xy}} \\ \end{matrix} \right) \left( \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right) \end{split}\]

10.3.2. Materiály izotropní v jedné rovině#

Materiály izotropní v jedné rovině (též uniaxiální, transerzálně symetrické, …) jsou materiály podobné ortotropním, ale ve dvou ze tří směrů mají stejné materiálové vlastnosti a díky tomu mají stejné vlastnosti ve všech směrech této roviny. Typickým představitelem jsou sendvičové materiály, například geologické vrstvy.

Konstanty související s izotropií jsou stejné. Například pro materiál izotropní v rovině \(xy\) vypadá materiálový vztah následovně.

\[\begin{split}\left( \begin{matrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \varepsilon_{yz} \\ \varepsilon_{xz} \\ \varepsilon_{xy} \end{matrix} \right) = \left( \begin{matrix} S_{11} & S_{12} & S_{13} & 0 & 0 & 0 \\ & S_{11} & S_{13} & 0 & 0 & 0 \\ & & S_{33} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ \rlap{\text{symmetric}} & & & & S_{44} & 0 \\ & & & & & S_{66} \\ \end{matrix} \right) \left( \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right) \end{split}\]

Tyto materiály popisujeme pomocí pěti nezávislých materiálových konstant. Šestá konstanta je dána vztahem

\[S_{66} = 2(S_{11}-S_{22}).\]

10.3.3. Izotropní materiály#

Izotropní materiály mají ve všech směrech stejné vlastnosi.

\[S_{11}=S_{22}=S_{33}=\frac 1E, \quad S_{ij}=-\frac{\nu}{E} \text {pro $i\neq j$, $i,j\in\{1,2,3\}$}\]
\[S_{44}=S_{55}=S_{66}=\frac 1G\]
\[\begin{split}\left( \begin{matrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \varepsilon_{yz} \\ \varepsilon_{xz} \\ \varepsilon_{xy} \end{matrix} \right) = \left( \begin{matrix} S_{11} & S_{12} & S_{12} & 0 & 0 & 0 \\ & S_{11} & S_{12} & 0 & 0 & 0 \\ & & S_{11} & 0 & 0 & 0 \\ & & & S_{44} & 0 & 0 \\ \rlap{\text{symmetric}} & & & & S_{44} & 0 \\ & & & & & S_{44} \\ \end{matrix} \right) \left( \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right) \end{split}\]

Pomocí Youngova modulu, smykového modulu a Poissonova čísla dostáváme následující vztah.

\[\begin{split}\left( \begin{matrix} \varepsilon_x \\ \varepsilon_y \\ \varepsilon_z \\ \varepsilon_{yz} \\ \varepsilon_{xz} \\ \varepsilon_{xy} \end{matrix} \right) = \left( \begin{matrix} \frac 1E & -\frac{\nu}{E} & -\frac{\nu}{E} & 0 & 0 & 0 \\ & \frac 1E & -\frac{\nu}{E} & 0 & 0 & 0 \\ & & \frac 1E & 0 & 0 & 0 \\ & & & \frac 1G & 0 & 0 \\ \rlap{\text{symmetric}} & & & & \frac 1G & 0 \\ & & & & & \frac 1G \\ \end{matrix} \right) \left( \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right) \end{split}\]

Izotropní materiály charakterizujeme pomocí tří materiálových konstant. Mezi těmito konstantami je vztah

\[G = \frac{E}{2(1+\nu)}.\]
Hodnota \(\nu\) pro inzotropní materiály je zpravidl blízká číslu \(0.33\).

10.4. Přímé nosníky#

  • Posouvající síla a ohybový moment u nosníků.

  • Diferenciální rovnice ohybové čáry nosníku

Obsah