33. Geometrická posloupnost

Napiš kód, který modeluje růst geometrickou řadou z počáteční hodnoty \(X(0)=X_0\) s kvocientem \(r\), tj.

\[X(n+1)=r X(n), \quad X(0)=X_0.\]

Simulaci proveďte pro třicet generací, tj. pole \(X\) bude mít třicet prvků.

Použijeme obvyklou strukturu.

1. Zavedení knihoven

2. Nastavení parametrů výpočtu

3. Vytvoření proměnných a nastavení počátečních hodnot

4. Výpočet modelu

Model je přednastaven, musíte dopsat množinu, přes kterou se iteruje, a výpočet následující hodnoty z hodnoty předchozí.

Pokud neodpovíte správně ani na několikátý pokus, můžete otázku vzdát a ukončit. Tímto dostanete možnost zobrazit si správnou odpověď. Zkopírujte si tuto odpověď do schránky, budete z ní vycházet v dalším příkladě.

Tip. Pokud úlohu vyřešíte, můžete proměnnou X vykreslit použitím následujících příkazů.

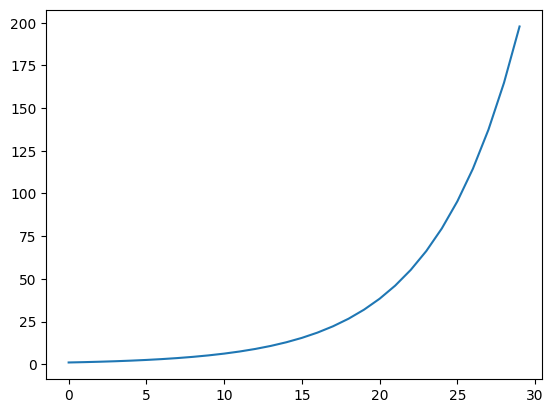
Graf bude vypadat následovně.

# zavedení knihoven
import numpy as np

# parametry modelu
X0 = 1
r = 1.2
N = 30

# inicializace proměnných
X = np.ones(N)
X[0] = X0

# Opravte následující model (množina pro iterace a iterační vztah pro další generaci)
for i in range(4):
    X[i+1] = 3