10. Trofické funkce

Při modelování se často setkáváme s tím, že odezva systému je modelována pomocí speciálních funkcí. Například působení predátora na kořist může být definováno funkcemi typu

\[f(x) = \frac{x}{x+k} \tag{1}\]

nebo typu

\[f(x) = \frac{x^2}{x^2+k}.\tag{2}\]

První typ se nazývá Holling II, druhý typ Holling III. Každý typ má své místo, například typ III se používá, pokud je dravec neúspěšný v lovu malé populace. Toto využíváme v případě, že kořist má možnost se ukrýt.

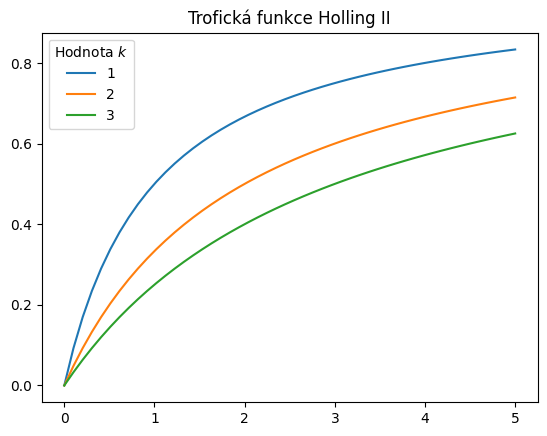
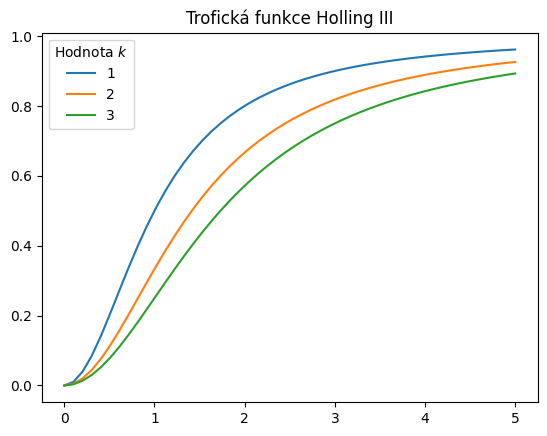
Přednastavený kód kreslí průběh trofické funkce Holling II (vzorec (1)) pro některé hodnoty parametru. Modifikujte ukázku tak, aby se kreslila trofická funkce Holling III (vzorec (2)). Modifikujte i nadpis grafu, aby byl v pořádku.

Nic dalšího neměňte. Opravte jenom dva řádky: Řádek, kde se definuje nadpis a řádek, kde je zadán vzorec pro výpočet funkce. Nemusíte kódu plně rozumět slovo od slova, ale měli byste být schopni identifikovat, které řádky je nutné změnit.

Výstup by se měl změnit následovně.

Popis	Obrázek
Původní obrázek
Nový obrázek

import numpy as np
import matplotlib.pyplot as plt

dolni_mez = 0
horni_mez = 5
seznam_k = [1,2,3]
nadpis = "Trofická funkce Holling II"

t = np.linspace(dolni_mez, horni_mez)

for k in seznam_k:
    y = t/(t+k)
    plt.plot(t,y)
plt.legend(seznam_k, title="Hodnota $k$")
plt.title(nadpis)