11. Vektorizace matematických operací

11.1. Teorie

Vektorizace matematických operací je technika, která umožňuje efektivně provádět matematické (ale i jiné) operace na celých souborech dat současně. Tím se eliminuje potřeba iterovat přes jednotlivé prvky souboru a provádět operace postupně. Namísto postupného zpracovávání jednotlivých prvků souboru je vektorizace schopna aplikovat operace na celý soubor jako celek. To vede ke kratšímu kódu, který se snadněji udržuje. Výpočet s velkými objemy dat je při vektorizaci rychlý, protože využívá výpočetních schopností moderních procesorů, které jsou optimalizovány pro práci s vektory dat.

V jazyce Python jsou nástroje pro vektorizaci v kníhovně NumPy.

11.2. Vektorizace pro vektor zadaný po složkách

Představme si, že máme vektor x, který obsahuje hodnoty populace v čase, a konstanty r a K. Chceme aplikovat funkci logistického růstu, tj. funkci

\[rx\left(1-\frac xK\right),\]

na všechny hodnoty vektoru x najednou pomocí vektorizace.

import numpy as np

# Vstupní hodnoty
x = np.array([0.1, 0.3, 0.5, 0.7])
r = 0.8
K = 1.0

# Logistický růst pomocí vektorizace
y = r * x * (1 - x / K)

Výstupem bude vektor y, který obsahuje vypočítané hodnoty logistického růstu pro každý prvek vektoru x. Každá operace (*, -, /) je aplikována na celý vektor najednou, díky čemuž je kód kratší a rychlejší.

11.3. Vektorizace pro vektor vygenerovaný příkazem np.linspace

Ve výše uvedeném příkladě je vektor x zadán z klávesnice. V praxi se pracuje s dlouhými seznamy dat, kdy jsou data buď načtena z externího souboru, nebo vygenerována příslušnými příkazy. Například následující kód vygeneruje díky přítomnosti příkazu np.linspace do proměnné x celkem 500 bodů rovnoměrně rozdělených na intervalu od 0 do 5 a každý tento bod dosadí do funkce

\[\frac{x^2}{x^2+1},\]

která se v ekologii používá pro modelování působení populace predátora na populaci kořisti. Praktické použití je například při kreslení grafu, kdy pro kreslení potřebujeme dostatek dat.

import numpy as np  # knihovna pro numerické výpočty
import matplotlib.pyplot as plt  # knihovna pro kreslení grafů
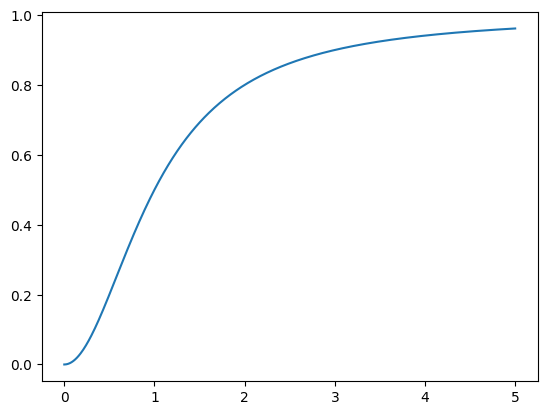
x = np.linspace(0,5,500)  # 500 hodnot na vstupu
y = x**2/(x**2+1) # výpočet pro všech 500(!!!) vstupních hodnot
plt.plot(x,y) # graf pro kontrolu

Výstupem kódu je 500 funkčních hodnot v proměnné y, které po vykreslení vedou na následující graf.

11.4. Úkol

V poli je přednastaven kód pro rychlost růstu v prostředí s omezenou nosnou kapacitou (logistický růstem). Upravte kód tak, aby pro výpočet funkčních hodnot použil více bodů namísto čtyř explicitně zadaných. Do proměnné x vložte 500 rovnoměrně rozložených hodnot z intervalu \([0,1]\).

import numpy as np

# Vstupní hodnoty
x = np.array([0.1, 0.3, 0.5, 0.7])
#      ^^^ nahradit za np.linspace se spravnymi parametry 
r = 0.8
K = 1.0

# Logistický růst pomocí vektorizace
y = r * x * (1 - x / K)

TIP: Pokud přidáte následující kód na konec skriptu, zobrazí se graf funkce. Pro čtyři hodnoty se bude jednat o lomenou čáru, pro 500 hodnot půjde o hladkou křivku.

import matplotlib.pyplot as plt
plt.plot(x,y)