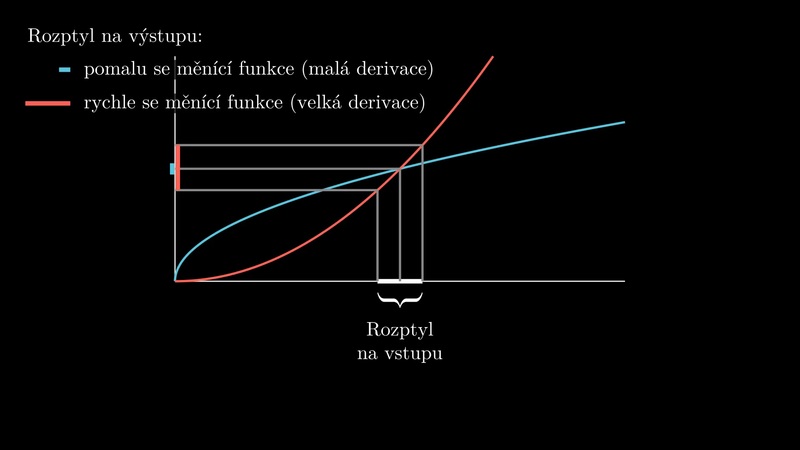
Derivace a lineární aproximace

2. Derivace a lineární aproximace#

Minivideo

Připomenutí derivací z ptačí perspektivy

S využitím aparátu derivací jsme v minulé přednášce poznali a naučili nebo naučíme se ve cvičení řešit úlohy tří základních různých typů:

  1. K funkci najdi její derivaci, tj. rychlost změny. Toto je klasické derivování, případně doplněné o slovní interpretaci derivace. Použijeme vzorce a jedná se o čistě manuální dovednost. Vstupem je funkce, výstupem její derivace a případně slovní interpretace této derivace. Příkladů je spousta na webu i v učebnicích.

  2. Ze zadaného vztahu mezi dvěma veličinami najdi vztah mezi rychlostmi změn těchto veličin. Jako vedlejší produkt mimo jiné využíváme dovednosti derivování z předchozího bodu a vždy derivujeme složenou funkci: vzorec vyjadřující jednu veličinu pomocí druhé je vnější složka a druhá veličina, resp. její závislost na čase, je složka vnitřní. Vstupem je vztah mezi veličinami a rychlost, s jakou se jedna z veličin mění, výstupem je rychlost, s jakou se mění veličina druhá.

  3. Ze zadaného slovního popisu nějakého děje sestav matematický model. Ve slovním modelu je zmíněna rychlost, tu matematicky přepisujeme jako derivaci a tato rychlost je v nějaké relaci s ostatními veličinami. Odsud sestavujeme rovnici. Vstupem je mechanismus popisující vývoj systému, výstupem matematický model ve formě rovnice obsahující neznámou funkci popisující stav systému a její derivaci. V průběhu semestru se takovéto rovnice naučíme řešit, nejprve se však detailněji koukneme na to, abychom poznali i další role derivace.

2.1. Aplikace derivací 3: Jak citlivě? (reakce na změnu)#

Minivideo
Derivace ukazuje, jak citlivě funkční hodnoty reagují na změny ve vstupních datech. Pokud jsou například vstupní data pro funkci produktem nějakého měření, zjistíme, jak se nepřesnosti v tomto měření projeví na nepřesnostech vypočtených funkčních hodnot. Otevřít prezentaci

Derivace v bodě, pokud ji nahlížíme z hlediska citlivosti reakce funkce na změnu vstupních dat, udává, jaký vliv má jednotková změna ve vstupních datech na změnu funkční hodnoty funkce. Pokud změna ve vstupních datech není jednotková ale násobek jednotkové změny, je i odezva násobná.

Poznámka (Derivace jako měřítko citlivosti funkce na změnu vstupních dat)

Buď \(\displaystyle f:\mathbb R\to\mathbb R\) funkce taková, že má derivaci. Pokud se veličina \(\displaystyle x\) změní z hodnoty \(\displaystyle x_0\) o hodnotu \(\displaystyle \Delta x\) (tj. nová hodnota je \(\displaystyle x_0+\Delta x\)), potom se \(\displaystyle f\) mění přibližně o \(\displaystyle f'(x_0)\Delta x\), tj.

\[\Delta f\approx f'(x_0)\Delta x\]
neboli
\[\Delta f\approx \frac{\mathrm df(x_0)}{\mathrm dx}\Delta x.\]
Tato aproximace je použitelná pro malé hodnoty \(\displaystyle \Delta x\).

Co se rozumí malou hodnotou \(\displaystyle \Delta x\) závisí na více faktorech, například i na tom, jak se funkce „vzpírá“ tomu, být aproximována výrazem úměrným \(\displaystyle \Delta x\). Přesněji tuto podmínku zformulujeme po probrání Taylorova polynomu, kdy se použije o něco obecnější postup.

Příklad. Nosník výšky \(\displaystyle h\), šířky \(\displaystyle a\) a délky \(\displaystyle L\) je uprostřed zatížený silou \(\displaystyle F\). Průhyb \(\displaystyle s\) uprostřed nosníku je dán vztahem

(2.1)#\[s=\frac {F L^3}{4Eah^3},\]

kde \(\displaystyle E\) je materiálová konstanta. Pro \(\displaystyle h=20\,\mathrm{cm}\) je průhyb \(\displaystyle s=10\,\mathrm{cm}\). Zjistěte, jak se průhyb mění při změnách výšky nosníku. Odhadněte, jak se průhyb změní, pokud se \(\displaystyle h\) sníží na \(\displaystyle 18\,\mathrm{cm}\)?

Řešení. Relevantními veličinami jsou \(\displaystyle s\) a \(\displaystyle h\) a vzorec je tedy možno shrnout do tvaru

\[s=\frac k{h^3},\]
kde \(\displaystyle k\) je konstanta charakterizující danou situaci. Pro zadané hodnoty výšky a průhybu vychází konstanta
\[k=s h^3=10\times 20^3=80\,000.\]
Vzorec (2.1) tedy redukujeme na
\[s={80\,000}{h^{-3}}.\]
Derivováním obdržíme
\[\frac{\mathrm ds}{\mathrm dh}=80\,000\times(-3) h^{-4}=-\frac{3\times 80\,000}{h^4}.\]
Změna výšky nosníku je
\[\Delta h=18-20=-2\,\mathrm{cm}\]
a tomu odpovídá změna průhybu
\[\Delta s=-\frac{3\times 80\,000}{(20)^4}(-2)=3\,\mathrm{cm}.\]
Průhyb se tedy zvětší o \(\displaystyle 3\,\mathrm{cm}\).

Poznámka (Smysl předchozího příkladu)

Proč nepočítáme přesně? Stačila by selská logika a změna funkce \(\displaystyle s=\frac k{h^3}\) by byla

(2.2)#\[\Delta s=\frac k{(h+\Delta h)^3}-\frac k{h^3}.\]

Odpověď je překvapivá: pomocí derivací je vyjádření změny v naprosté většině případů jednodušší. V tomto našem případě máme

\[\Delta s\approx -\frac{3k}{h^4}\Delta h,\]
což je na další práci mnohem příjemnější výraz, než rozdíl dvou zlomků (2.2). Skutečnost, že platí pouze pro malé \(\displaystyle \Delta h\) nás nijak neomezuje. Většinou se tento aparát používá tam, kde se chyba limitním přechodem „stáhne na nulu“. Navíc, ukazujeme koncept. Důležité je si z příkladu odnést, že derivace umožní analyzovat, jak vypočítané veličiny reagují na změny ve vstupních datech. Výsledkem může být například maximální teoretická přesnost se kterou je možné vypočítat výslednou veličinu při vstupních datech zatížených chybou nebo nějakým způsobem nejistých (zákon šíření chyb).

Úkol

2.2. Lineární aproximace#

Minivideo

V následujících pasážích se budeme věnovat lineární aproximaci funkce. To je nahrazení funkce s jakkoli složitým funkčním předpisem funkcí s tím nejjednodušším možným předpisem: lineární funkcí. Tím se pochopitelně dopouštíme jisté nepřesnosti a je to něco za něco: k popisu úlohy máme poté k dispozici jednodušší funkce, ale výpočty jsou zatíženy chybou. Někdy tato chyba může být tak velká, že je idea lineární aproximace naprosto nepoužitelná. Ale jindy se jedná o nástroj, který prakticky neřešitelnou úlohu převede na úlohu snadno zvládnutelnou. Linearizace nelineárních úloh je jedním ze základních inženýrských postupů. V mnoha případech dává samotná dobré výsledky a řeší zadaný problém, v jiných případech slouží jako odrazový můstek ke zvládnutí nelineárního problému.

2.2.1. Lineární aproximace v 1D#

Pokud se funkce mění, můžeme odhad změny z předchozího odstavce přičíst k funkční hodnotě a tím máme odhad funkční hodnoty po změně. Toto je principem lineární aproximace, neuvěřitelně jednoduché a přitom velice mocné techniky používané inženýry k tomu, aby se popis problémů a řešení úloh vůbec daly efektivně zvládnout.

Věta (Lineární aproximace)

Buď \(\displaystyle f:\mathbb R\to\mathbb R\) funkce, která má derivaci. V okolí bodu \(\displaystyle x_0\) platí přibližný vzorec

\[f(x)\approx f(x_0)+ f'(x_0)(x-x_0)\]
neboli
\[f(x)\approx f(x_0)+ \frac{\mathrm df(x_0)}{\mathrm dx}(x-x_0).\]

Poznámka (Slovní interpretace vzorce pro lineární aproximaci)

Výše uvedený vzorec není těžké rozšifrovat.

  • Veličina \(\displaystyle f(x)\) je funkční hodnota v bodě \(\displaystyle x\), tu chceme odhadnout.

  • Veličina \(\displaystyle f(x_0)\) je známá funkční hodnota v bodě \(\displaystyle x_0\), to je ýchozí bod pro odhad.

  • Veličina \(\displaystyle f'(x_0)\) je odhad změny veličiny \(\displaystyle f\) způsobený jednotkovou změnou vstupních dat (zvýšení hodnoty \(\displaystyle x_0\) o jednotku). Tento faktor ještě v dalším kroku musíme přizpůsobit tomu, že změna vstupních dat není jednotková, což uděláme s využitím přímé úměrnosti.

  • Veličina \(\displaystyle f'(x_0)(x-x_0)\) je odhad změny veličiny \(\displaystyle f\) vyvolané změnou veličiny \(\displaystyle x\) z \(\displaystyle x_0\) o \(\displaystyle \Delta x=x-x_0\) tak, jak jsme jej používali v minulé přednášce.

Poznámka (Alternativní vzorec pro lineární aproximaci)

Vzorec pro lineární aproximaci se často píše v ekvivalentním tvaru

\[f(x+h)\approx f(x)+f'(x)h,\]
což získáme dosazením \(\displaystyle x+h\) za \(\displaystyle x\) a \(\displaystyle x\) za \(\displaystyle x_0\).

Poznámka (Význam vzorce pro lineární aproximaci)

  • Vzorec umožňuje složitý funkční předpis předpisem jednodušším (lineární funkce jsou jedny z nejtrivilálnějších).

  • K použití vzorce stačí znát jeden bod grafu a funkční hodnotu a hodnotu derivace v tomto bodě.

  • Aproximace je pouze lokální, použitelná pouze v určitém okolí uvažovaného bodu. Jak velké toto okolí může být a jaké chyby se dopouštíme při lineární aproximaci je různé pro různé funkce. Obecně platí, že čím blíže jsme k bodu \(\displaystyle x_0\), tím je tato aproximace přesnější.

../_images/linapprox.svg

Obr. 2.1 Následující obrázek demonstruje skutečnost, že lineární aproximace je pouze lokální. Funkce sinus má nelineární graf a žádná lineární funkce ji nemůže aproximovat na celém definičním oboru. Pokud se však zaměříme na malý kousek grafu (žlutý obdélník), je lineární aproximace možná a použitelná.#

Příklad (růst stromu). Strom má v roce 2019 výšku 3 metry a roste rychlostí 0.5 metru za rok. V roce \(\displaystyle x\) je jeho výška dána vzorcem

\[h(x)=3+0.5(x-2019).\]

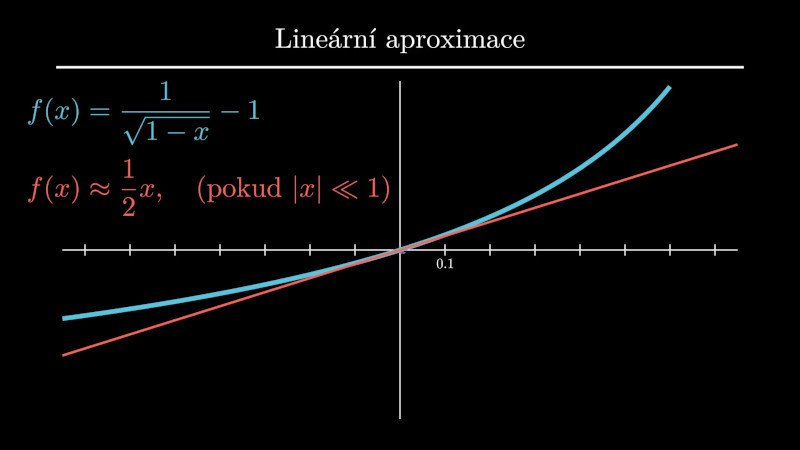
Příklad (aproximace důležitých funkcí v okolí nuly). Ve cvičení ukážeme platnost následujících přibližných vzorců, které platí pro \(\displaystyle x\) blízké k nule.

\[\sin x\approx x, \quad \cos x\approx 1,\qquad (1+x)^n\approx 1+nx.\]
První dva vzorce využijeme později při popisu malých rotací v rovině. Mnoho důležitých aplikací těchto vzorců ve fyzice je na webu fyzikální olympiády v dokumentu Aproximace ve fyzikálních úlohách.

Lineární aproximace může pomoci zjednodušit komplikované funkční vztahy v případě, kdy vstupní data nejsou příliš variabilní. Otevřít prezentaci Spustit video
Úkol Úkol

2.2.2. Lineární aproximace v některých fyzikálních zákonech#

../_images/chimborazo.jpg

Obr. 2.2 Vrcholek hory Chimborazo je místo nejvzdálenější od středu Země. Roli hraje nadmořská výška a zploštění Země. Gravitační zrychlení zde je nejmenší. Zdroj: pixabay.com#

Příklad (gravitační potenciál v malých výškách nad zemí). Gravitační potenciál \(\displaystyle V\) ve vzdálenosti \(\displaystyle r\) od středu koule o hmotnosti \(\displaystyle M\) je dán vztahem

\[V(r)=-G\frac Mr=-GMr^{-1},\]
kde \(\displaystyle G\) je gravitační konstanta. Najdeme lineární aproximaci v bodě \(\displaystyle R\).

Dosazením obdržíme

\[V(R)=-GMR^{-1}\]
a derivováním
\[\frac{\mathrm dV}{\mathrm dr}=GMr^{-2}, \quad \frac{\mathrm dV(R)}{\mathrm dr}=GMR^{-2}. \]
Odsud poté získáme lineární aproximaci
\[V(r)\approx -GMR^{-1}+GMR^{-2}(r-R)\]
Pro Zemi jako kouli o poloměru \(\displaystyle R\) je \(\displaystyle r-R\) výška nad Zemí \(\displaystyle h\) a aproximaci je možno po přeznačení napsat ve tvaru
\[V(r)\approx V_0 +gh.\]
V tomto označení je \(\displaystyle V_0=-GMR^{-1}\) konstanta související s volbou nulové hladiny potenciálu a vzhledem k libovolnosti volby nulové hladiny je tato hodnota nepodstatná. Veličina \(\displaystyle g=GMR^{-2}\) je tíhové zrychlení vyjádřené pomocí gravitační konstanty \(\displaystyle G\) a parametrů Země. Veličina \(\displaystyle gh\) je potenciál v tíhovém poli Země. Tuto veličinu známe lépe ze vzorce pro potenciální energii tělesa o hmotnosti \(\displaystyle m\), který má tvar
\[E=mgh.\]

Online výpočet tíhového zrychlení

Příklad (potenciální a kinetická energie). V předchozím příkladě je možné využít vztah

\[(1\pm x)^n\approx 1\pm nx ,\quad \text{pro malé }x.\]
Přepsáním gravitačního potenciálu \(\displaystyle V\) do tvaru obsahujícího výšku nad zemí \(\displaystyle h\) a využitím lineární aproximace získáme
\[V = -G \frac{M}{R+h} =-G \frac{M}{R}\left (1+\frac hR\right)^{-1} \approx -G \frac MR\left(1+(-1)\frac hR\right) =-G \frac{M}{R} + G \frac{M}{R^2} h\]
a po zavedení nových konstant
\[ V\approx V_0+ g h,\]
kde \(\displaystyle g=G \frac{M}{R^2}\).

Podobně aproximací přesných vztahů plynoucích z Einsteinovy teorie relativity získáme složku energie související s pohybem, tj. kinetickou energii

\[E=\frac{m_0c^2}{\sqrt{1-\frac {v^2}{c^2}}} =m_0 c^2 \left(1-\frac {v^2}{c^2}\right)^{-1/2} \approx m_0 c^2 \left(1+\left(-\frac 12\right)\left(-\frac {v^2}{c^2}\right)\right)=m_0c^2+\frac 12 m_0v^2 \]
pro \(\displaystyle v\) mnohem menší než \(\displaystyle c\). Snadno rozšifrujeme, že s rychlostí souvisí jenom druhý sčítanec a že se jedná o klasický vzorec pro kinetickou energii \(\displaystyle \frac 12 mv^2\).

Ač se jedná „jenom“ o lineární aproximaci, je vzorec \(\displaystyle E=\frac 12 mv^2\) dokonce mnohem použitelnější, protože výpočet kinetické energie pomocí univerzálně platného relativistického vzorce při malých rychlostech v praxi obvykle zhavaruje na zaokrouhlovacích chybách.

2.3. Lineární aproximace a jednorozměrné materiálové vztahy#

Minivideo
../_images/Stress_Strain_Ductile_Material.jpg

Obr. 2.3 Podnět a materiálová odezva v případě mechanického namáhání oceli s malým obsahem uhlíku. Pěkně vidíme lineární závislost v okolí počátku a odklon od lineární závislosti pro velké namáhání. Zdroj: https://en.wikipedia.org, Breakeydown#

V inženýrské praxi často potřebujeme modelovat odezvu materiálu reagujícího na vnější podnět. Může se jednat například o změnu délky při mechanickém namáhání, tok tepla materiálem při tepelném namáhání, tok tekutiny porézním materiálem (dřevo, půda) při difuzi nebo rozdílu tlaků a podobně.

Pokusíme se modelovat funkci dávající do souvislosti velikost podnětu a reakci materiálu.

  • Je přirozené, že při nulovém podnětu není žádná odezva a proto funkce prochází počátkem.

  • S velikostí podnětu odezva na tento podnět roste a proto funkce v okolí počátku má kladnou derivaci a roste.

  • Z lineární aproximace vidíme, že pro \(\displaystyle x_0=0\) a \(\displaystyle f(0)=0\) se vzorec pro lineární aproximaci redukuje na

    \[f(x)\approx f'(0)x,\]
    tj. na přímou úměrnost.

  • Ukazuje se, že v řadě praktických úloh je uvedená aproximace dobrá na dostatečně dlouhém intervalu a podle typu úlohy má tato aproximace povahu fyzikálního zákona a svůj vlastní název. Nejčastěji se setkáme se s Hookovým zákonem pro deformaci materiálu (relativní prodloužení je úměrné normálovému napětí), Darcyho zákonem pro tok tekutiny půdou (filtrační rychlost je úměrná záporně vzatému hydraulickému gradientu), Fickovým zákonem pro difuzi (hustota difuzniho toku je úměrná záporně vzatému gradientu koncentrace) a Fourierovým zákonem pro vedení tepla v materiálu (hustota tepelného toku je úměrná záporně vzatému gradientu teploty). Později, v přednášce o zákonech zachování ve vektorovém poli ke konci semestru, si tyto závislosti naformulujeme ve vícerozměrném prostředí a hlavně ve tvaru, který umožní zohlednit práci s neizotropními materiály (různé fyzikální vlastnosti v různých směrech).

  • Matematicky je tedy povaha přímé úměrnosti v materiálových vztazích zřejmá a experimentálně je možné ověřit, pro jaké oblasti platí. Toto nám však mnohdy nestačí a snažíme se tyto vztahy ještě odvodit ze základních fyzikálních vztahů a z představy jak daný proces funguje. To otevírá možnosti potvrdit si, že naše představa o chování materiálu je správná.

  • V některých velmi speciálních případech dokonce umíme určit materiálovou charakteristiku výpočtem namísto měření. Pro praktické využití tato dovednost není významná (můžeme vypočítat například koeficient filtrace pro půdu složenou z částic ve tvaru stejně velkých kuliček, v praxi se však s takovým materiálem setkáme nanejvýš při speciálních aplikacích v laboratoři), ale dává nám to důležitý prostor pro ověření fyzikálních hypotéz a matematických postupů.

Úkol

2.4. Derivace a tečna#

Lineární aproximace funkce je vlastně aproximace tečnou. Protože pojem tečna ze střední školy chápeme jenom intuitivně, můžeme nyní pomocí derivace tečnu dokonce definovat. Z geometrického pohledu je tečna přímka bodem \(\displaystyle [x_0,f(x_0)]\), která má směrnici \(\displaystyle f'(x_0)\). Proto se o derivaci často mluví jako o směrnici tečny.

Definice (Tečna)

Nechť \(\displaystyle f\) je funkce, která má v bodě \(\displaystyle x_0\) derivaci \(\displaystyle f(x_0)\). Přímka

\[y=f(x_0)+f'(x_0)(x-x_0)\]
se nazývá tečna ke grafu funkce \(\displaystyle f\) v bodě \(\displaystyle x_0\).

Díky souvislosti derivace s tečnou je derivace jedinečným nástrojem při popisu vlastností křivek. Příslušná oblast se nazývá diferenciální geometrie a je to jakási oblast mezi geometrií a diferenciálním počtem.

2.5. Aproximace vyššího řádu#

Minivideo

2.5.1. Motivace: Je možné chtít více než je lineární aproximace?#

../_images/laser.jpg

Obr. 2.4 Teorie založené na lineárních aproximacích vyřešily mnoho důležitých úloh, ale pokud by příroda fungovala lineárně jako celek, nemohli bychom sestrojit například laser. Ten je založený na nelineární optice a materiálech s nelineární materiálovou odezvou. Neměli bychom řezací stroje, ale ani laserová ukazovátka. Zdroj: pixabay.com#

Lineární aproximace vychází z předpokladu, že rychlost růstu (nebo poklesu) se příliš nemění. Někdy můžeme mít dodatečnou informaci o tom, jak se tato rychlost změní. Například pokud se bude rychlost zpomalovat, bude skutečná hodnota funkce menší než lineární aproximace.

Je otázka, zda a jak je možné informaci o tom, jak rychle roste rychlost, případně jak rychle roste rychlost růstu rychlosti, využít. To znamená že budeme studovat derivaci derivace, derivaci derivace derivace atd.

Aproximaci funkce \(\displaystyle \cos x\approx 1\) zmíněnou výše (odvodíme ve cvičení), kdy aproximujeme vlastně konstantní funkcí, je možné také chápat jako selhání lineární aproximace. Následující slidy a pojem Taylorův polynom nám umožní najít prostředek pro aproximaci i v těchto případech.

2.5.2. Derivace vyšších řádů#

Definice (Druhá a další vyšší derivace)

  • Druhou derivací rozumíme derivaci derivace. Označujeme \(\displaystyle f''(x)\) nebo \(\displaystyle \frac{\mathrm d^2 f}{\mathrm dx^2}\).

  • Podobně \(\displaystyle k\)-tou derivací rozumíme derivaci \(\displaystyle (k-1)\)-ní derivace. Označujeme \(\displaystyle f^{(k)}(x)\) nebo \(\displaystyle \frac{\mathrm d^k f}{\mathrm dx^k}\).

Platí tedy

\[\frac {\mathrm d^2 f}{\mathrm dx^2}:=\frac {\mathrm d}{\mathrm dx} \left(\frac {\mathrm d f}{\mathrm dx}\right),\quad \frac {\mathrm d^kf}{\mathrm dx^k}:=\frac {\mathrm d}{\mathrm dx} \left(\frac {\mathrm d^{k-1}f}{\mathrm dx^{k-1}}\right) \]
aneb
\[f'':=(f')', \quad f'''=(f'')', \quad f^{(k)}={(f^{(k-1)})'}.\]

Označení derivací pomocí čárek se nazývá Lagrangeova notace, označení pomocí podílu diferenciálů Leibnizova notace. Ještě se někdy používá i Eulerova notace, používající \(\displaystyle \mathrm Df\), \(\displaystyle \mathrm D^2 f\) a \(\displaystyle \mathrm D^k f\) pro první, druhou a \(\displaystyle k\)-tou derivaci.

Příklad.

  • Exponenciální funkce \(\displaystyle e^x\) má všechny derivace stejné.

  • U mocninné funkce se každým derivováním sníží exponent. Je-li exponentem přirozené číslo, po konečném počtu kroků se exponent sníží na nulu, funkce tedy bude konstantní a všechny další derivace budou nulové.

  • Polynomy mají všechny derivace od jistého řádu rovny nule.

Podobně je možné pracovat s parciálními derivacemi parciálních derivací. Například

\[\frac{\partial ^2 f}{\partial x^2}:=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial x}\right)\]
\[\frac{\partial ^2 f}{\partial y^2}:=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial y}\right)\]
nebo
\[\frac{\partial ^2 f}{\partial x\partial y}:=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right).\]

2.5.3. Druhá derivace a deformace nosníků#

../_images/nosniky.jpg

Obr. 2.5 Druhé derivace nám umožňují popsat tak zásadní věc, jako je chování nosníků při zátěži. Zdroj: pixabay.com#

Derivace hrají ústřední roli v teorii studující tuhost, deformaci a odolnost proti selhání u nosníků. Máme-li nosník podepřený na koncích a zatížený silou kolmo na podélnou osu nosníku (například vodorovný nosník se svislým zatížením) a je-li \(\displaystyle v(x)\) výchylka od rovnovážného stavu v bodě \(\displaystyle x\), potom derivace \(\displaystyle \frac{\mathrm dv}{\mathrm dx}\) vyjadřuje úhel pootočení svislého průřezu nosníku vlivem deformace a druhá derivace \(\displaystyle \frac{\mathrm d^2v}{\mathrm dx^2}\) při malých deformacích vyjadřuje křivost nosníku. Z fyzikálních úvah a ze vztahu mezi křivostí a momentem \(\displaystyle M(x)\) síly, která nosník deformuje, je možné odvodit rovnici

\[M(x)=EI\frac{\mathrm d^2v}{\mathrm dx^2},\]
kde konstanta \(\displaystyle E\) souvisí s materiálem (Youngův modul pružnosti) a \(\displaystyle I\) s průřezem nosníku (kvadratický moment průřezu). Podobně, pro nosník namáhaný v ose (například svislá vzpěra) silou \(\displaystyle F\) platí vztah
\[EI\frac{\mathrm d^2v}{\mathrm dx^2}+Fv=0.\]
Aplikace jsou, jak bylo uvedeno, při dimenzování nosníků (angl. beam buclinkg). Odvození výše uvedených rovnic není komplikované, ale vyžaduje dodatečné fyzikální znalosti a proto zde neuvádíme.

Někdy je vhodné mít moment \(\displaystyle M(x)\) síly deformující nosník mít vyjádřený pomocí zatížení nosníku. To souvisí s druhou derivací momentu a proto je nutno rovnici ještě dvakrát derivovat. Proto se ohybová rovnice nosníku někdy uvádí jako vztah obsahující dokonce čtvrtou derivaci.

2.5.4. Taylorův polynom a polynomiální aproximace v 1D#

Definice (Taylorův polynom)

Taylorův polynom stupně \(\displaystyle n\) pro funkci \(\displaystyle f\) v bodě \(\displaystyle x_0\) je polynom

\[T(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2!}f''(x_0)(x-x_0)^2+\cdots +\frac{1}{n!}f^{(n)}(x_0)(x-x_0)^n,\]
tj.
\[T(x)=f(x_0)+\frac {\mathrm df(x_0)}{\mathrm dx}(x-x_0)+\frac{1}{2!} \frac {\mathrm d^2f(x_0)}{\mathrm dx^2} (x-x_0)^2+\cdots +\frac{1}{n!}\frac {\mathrm d^nf(x_0)}{\mathrm dx^n}(x-x_0)^n.\]

Taylorův polynom je nejlepší aproximace funkce \(\displaystyle f\) polynomem. Je možné ukázat, že rozdíl

\[f(x)-T(x)\]
je blízký k nule, pokud je \(\displaystyle n\) dostatečně velké, \(\displaystyle x\) dostatečně blízko k \(\displaystyle x_0\) a \(\displaystyle (n+1)\)-ní derivace funkce \(\displaystyle f\) je relativně malá. V těchto případech je
\[f(x)\approx T(x).\]
V tomto případě dostáváme následující větu. V ní \(\displaystyle O((x-x_0)^{n+1})\) je takzvané Landauovo velké O. Tímto zápisem je vyjádřen člen, který je pro \(\displaystyle x\) blízká k \(\displaystyle x_0\) v absolutní hodnotě menší než násobek funkce \(\displaystyle (x-x_0)^{n+1}\), tj. v bodě \(\displaystyle x_0\) konverguje k nule stejně rychle nebo rychleji jako mocninná funkce s exponentem \(\displaystyle n+1\).

Věta (Taylorova aproximace v okolí nuly)

Platí

\[f(x)=T(x)+O((x-x_0)^{n+1}),\]
resp. pro \(\displaystyle x=x_0+h\)
\[f(x_0+h)=f(x_0)+f'(x_0)h+\frac{1}{2!}f''(x_0)h^2+\cdots +\frac{1}{n!}f^{(n)}(x_0)h^n+O(h^{n+1}),\]
pokud existují spojité derivace funkce \(\displaystyle f\) do řádu \(\displaystyle n+1\).

Často používáme aproximaci v nule. Potom dostáváme pro aproximaci v okolí nuly

\[f(x)=f(0)+f'(0)x+\frac{1}{2!}f''(0)x^2+\cdots +\frac{1}{n!}f^{(n)}(0)x^n+O(x^{n+1}).\]

Příklad.

\[\begin{split} \begin{aligned} \ln \frac{1+x}{1-x}&\approx 2x+\frac 23 x^3+\frac 25 x^5+\frac 27 x^7 +\frac 29 x^9\\ \ln 2=\ln\frac {1+\frac 13}{1-\frac 13}&\approx 0.69314604 \end{aligned}\end{split}\]
Po tomto výpočtu je prvních pět cifer aproximace \(\displaystyle \ln 2\) správně. Tady vidíme i jeden zajímavý trik. Pokud bychom se snažili napsat Taylorův polynom funkce \(\displaystyle \ln (x+1)\), která vypadá příjemněji, chyba aproximace by byla mnohem větší.

Online výpočet.

2.6. Konečné diference a numerická aproximace derivace#

Minivideo
../_images/diference.png

Obr. 2.6 V praxi často pracujeme s daty získanými po skocích. Místo spojité funkce (křivky) tedy máme funkci definovanou v bodech (diskrétní funkce). I zde je nutné mít možnost měření rychlosti změny, která je co nejvíce kompatibilní s derivací.#

../_images/pisarky.jpg

Obr. 2.7 Tramvajový most v Brně Pisárkách z předpjatého betonu. Vede do zatáčky a ve stoupání. Analyticky vyřešit namáhání takového mostu je nereálné, podobné úlohy se řeší převodem úlohy obsahující derivace na úlohy lineární algebry. Podobné síly mohou vznikat i v dřevěných konstrukcích a to i v případě, že nosníky primárně nekonstruujeme jako předpjaté. Zdroj: vlastní.#

Pro numerické řešení rovnic obsahujících derivace je vhodné umět nahradit derivace veličinami, se kterými se lépe pracuje v numerických výpočtech.

Základním přístupem je vynechání limitního přechodu v definici derivace

\[\frac{\mathrm df}{\mathrm dx}=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}.\]
Tedy
\[\frac{\mathrm df}{\mathrm dx}\approx\frac{f(x+h)-f(x)}{h}.\]
Okamžitá rychlost je nahrazena průměrnou rychlostí na intervalu \(\displaystyle (x,x+h).\) Tento podíl se nazývá dopředná poměrná diference. Analogicky je definována vztahem
\[\frac{\mathrm df}{\mathrm dx}\approx\frac{f(x)-f(x-h)}{h}\]
zpětná poměrná diference.

Lepší aproximace derivace vychází z Taylorova polynomu druhého řádu napsaného pro \(\displaystyle f(x+h)\) a \(\displaystyle f(x-h)\), tj. ze vztahů

\[\begin{split}\begin{aligned} f(x+h)&\approx f(x)+f'(x)h+\frac 12 f''(x)h^2,\\ f(x-h)&\approx f(x)-f'(x)h+\frac 12 f''(x)h^2. \end{aligned}\end{split}\]

  • Pokud tyto vztahy odečteme, dostaneme

    \[ f(x+h)-f(x-h)\approx2f'(x)h. \]
    a odsud dostáváme aproximaci první derivace pomocí centrální diference ve tvaru
    \[ \frac{\mathrm d f}{\mathrm dx}=f'(x)\approx \frac{f(x+h)-f(x-h)}{2h}.\]
    Protože používáme aproximaci kvadratickým polynomem, je aproximace derivace pomocí centrální diference přesnější než aproximace pomocí dopředné diference.

  • Pokud tyto vztahy sečteme, dostaneme

    \[ f(x+h)+f(x-h)\approx 2f(x)+ f''(x)h^2 \]
    a odsud dostáváme aproximaci druhé derivace
    \[ \frac{\mathrm d^2f}{\mathrm dx^2}=f''(x)\approx \frac{f(x-h)-2f(x)+f(x+h)}{h^2}. \]

Úkol Úkol

2.7. Odbočka: od vazeb mezi atomy k materiálovým vlastnostem#

../_images/table-detail.jpg

Obr. 2.8 Stůl z kompozitního materiálu. U řady materiálů je možné ze struktury vypočítat fyzikální vlastnosti ještě dříve, než tyto materiály vůbec vyrobíme. Zdroj: http://seiboncarbon.com.au#

Výraz

\[V(r)=\frac 1{r^{12}}-\frac 2{r^6}=r^{-12}-2r^{-6}\]
je (až na konstanty, které pro pohodlí volíme pevně) Lennard-Jonesův potenciál často používaný pro interakci mezi atomy nebo molekulami. Napíšeme Taylorův polynom druhého stupně v bodě \(\displaystyle r=1\). K tomu potřebujeme znát funkční hodnotu a hodnotu prvních dvou derivací v tomto bodě.
\[\begin{split}\begin{aligned} V(1)&=1-2=-1\\ \frac{\mathrm dV}{\mathrm dr}&=-12r^{-13}-2(-6)r^{-7}\Bigr|_{r=1}=-12+12=0\\ \frac{\mathrm d^2V}{\mathrm dr^2}&=12\cdot 13 r^{-14}-2\cdot6\cdot 7r^{-8}\Bigr|_{r=1}=12\cdot 13-12\cdot 7=72\\ V(r)&\approx -1+\frac 12 72 (r-1)^2 \end{aligned} \end{split}\]
Konstanta \(\displaystyle -1\) je nezajímavá, souvisí s nulovou hladinou potenciálu a nulovou hladinu potenciálu si můžeme volit libovolně.

Lineární člen chybí a kvadratický člen je analogický potenciální energii pružiny o tuhosti \(\displaystyle k\) ve tvaru

\[U=\frac 12 kx^2.\]
Molekuly či atomy popsané tímto potenciálem se chovají jako tělesa na pružině o tuhosti \(\displaystyle k=72\) kmitající okolo rovnovážné polohy odpovídající \(\displaystyle r=1\). Pro atom o hmotnosti \(\displaystyle m\) tedy například platí vzorec pro úhlovou frekvenci oscilací \(\displaystyle \omega = \sqrt{\frac km}\), odvozený původně pro těleso na pružině. Analogicky se chovají pružné konstrukce. V klidu jsou ve stavu s minimální potenciální energií a při vychýlení z tohoto stavu o malou hodnotu začínají kmitat.

  • Pokud aproximujeme potenciál pomocí Taylorova polynomu, z koeficientu u kvadratického člene můžeme určit frekvenci oscilací.

  • Dále můžeme tímto způsobem určit pevnost vazby a tím pro daný materiál určit Youngův modul pružnosti, tj. konstantu úměrnosti mezi deformací materiálu a tahovým nebo tlakovým napětí v materiálu.

  • Poloha rovnovážné polohy, resp. její závislost na teplotě (pokud bychom do matematického modelu dodali skutečné parametry i s jejich teplotní závislostí) zase definuje koeficient teplotní roztažnosti materiálu.

Takovým způsobem můžeme u materiálu se známou strukturou odhadnout fyzikální vlastnosti výpočtem. To je důležité, protože teoretické předpovídání vlastností materiálu otevírá cestu k navrhování nových materiálů s výhodnějšími vlastnostmi. materiál můžeme prozkoumat ještě dříve, než jej vyrobíme a dostaneme na stůl.

Online výpočet a obrázek.

2.8. Řešení rovnic#

Minivideo

V praxi se setkáváme s případy, kdy je znám výsledek po aplikování funkce na vstupní data a je nutné rekonstruovat tato vstupní data. Řešíme tedy rovnici, kde neznámá je argumentem funkce a je známa funkční hodnota. Pojmy nutné pro korektní formulaci a jednu z velmi rychlých přibližných metod řešení rovnic si představíme v následujících pasážích.

Nejprve se budeme zabývat tím, jestli se k funkční hodnotě dají vstupní data rekonstruovat jednoznačně (prostá funkce). Pokud ano, představíme si pravidlo, které toto přiřazení vstupních dat k výsledku po aplikaci funkce dokáže realizovat (inverzní funkce). A na závěr si ukážeme metodu, jak při řešení rovnic (resp. počítat funkční hodnoty inverzních funkcí) využít derivaci. To vede k velmi rychlé a velmi obecné metodě numerického řešení (Newtonova metoda).

2.8.1. Prostá funkce#

Někdy jsme v situaci, že známe výsledek po působení nějaké funkce a potřebujeme zrekonstruovat vstupní hodnotu. Řešíme tedy pro zadanou funkci \(\displaystyle f\) a hodnotu \(\displaystyle y_0\) rovnici

\[f(x)=y_0.\]
Řešení této rovnice, pokud existuje, nemusí být určeno jednoznačně. Pro funkce, pro které je určeno jednoznačně, zavádíme následující pojem.

Definice (Prostá funkce)

Nechť \(\displaystyle f\) je funkce a \(\displaystyle M\subseteq \mathrm{Dom}(f)\) podmnožina definičního oboru funkce \(\displaystyle f\). Řekneme, že funkce \(\displaystyle f\) je prostá, jestliže každý obraz má jen jediný vzor, tj. pro každé \(\displaystyle y_0\in f(M)\) existuje jediné \(\displaystyle x\in M\) s vlastností \(\displaystyle f(x)=y_0\). Nespecifikujeme-li množinu \(\displaystyle M\), máme na mysli, že uvedená vlastnost platí na celém definičním oboru funkce \(\displaystyle f\).

Věta (Rovnice s prostou funkcí)

Pokud je \(\displaystyle f\) prostá funkce a platí

\[f(x)=f(a),\]
potom platí \(\displaystyle x=a.\)

Příklad. Vlastnost být či nebýt prostá je zásadní pro vyslovení odpovědi na otázku, zda rovnice má jediné řešení, či zda řešení může být více.

  • Funkce \(\displaystyle \frac 1x\) je prostá a proto z rovnosti \(\displaystyle \frac 1x = \frac 15\) plyne \(\displaystyle x=5\).

  • Funkce \(\displaystyle x^2\) není prostá a proto z rovnosti \(\displaystyle x^2 = 7^2\) neplyne \(\displaystyle x=7\). Ve skutečnosti pro každou rovnici ve které není prostá funkce, potřebujeme speciální metodu. Proto máme speciální vzorec pro řešení kvadratické rovnice, nebo například speciální postupy pro řešení goniometrickcýh rovnic.

2.8.2. Inverzní funkce#

Inverzní úloha je tak trošku jako reverzní inženýrství. Máme výsledek a potřebujeme znát vstupní data. U funkcí to je supersnadné, u konstrukcí supersložité. Užitečné je ale obojí.

Definice (Inverzní funkce)

Nechť funkce \(\displaystyle f: A\to B\) je prostá. Pravidlo, které každému \(\displaystyle x\) z množiny \(\displaystyle f(A)\) přiřadí to (jediné) \(\displaystyle y\), pro které platí \(\displaystyle f(y)=x\) se nazývá inverzní funkce k funkci \(\displaystyle f\), označujeme \(\displaystyle f^{-1}\).

Poznámka (Inverzní funkce pří řešení rovnic)

Jinak zapsáno, je-li

\[f(y)=x\]
a \(\displaystyle f\) má inverzní funkci, platí
\[y=f^{-1}(x).\]
Jedná se o zobecnění pouček jak „převádět výrazy na druhou stranu rovnice“.

Symbol \(\displaystyle f^{-1}(x)\) lze tedy chápat buď jako hodnotu inverzní funkce k funkci \(\displaystyle f\) v bodě \(\displaystyle x\), nebo jako převrácenou hodnotu k číslu \(\displaystyle f(x)\), tj jako \(\displaystyle [f(x)]^{-1}=\frac{1}{f(x)}\). Nebude-li z kontextu zřejmé, o kterou variantu se jedná, musíme toto upřesnit.

Příklad. Funkce \(\displaystyle y=x^2\) není prostá na \(\displaystyle \mathbb R\) a proto zde nemá inverzní funkci. Pokud definiční obor funkce \(\displaystyle y=x^2\) zúžíme na nezáporná čísla, tj. požadujeme \(\displaystyle x\geq 0\), je taková funkce prostá a má inverzní funkci. Protože tato úloha má praktický význam, vyplatí se pro tuto inverzní funkcí zavést speciální označení. Jak dobře víme, inverzní funkcí je druhá odmocnina, tj. funkce \(\displaystyle y=\sqrt x\).

2.8.3. Newtonova metoda#

Newtonova metoda (též Newtonova Raphsonova metoda) je metoda pro numerické řešení rovnic. To používáme v případě, že není možné (nebo není účelné) řešit rovnici přesně a snažíme se najít přibližné řešení. Například neznáme inverzní funkci, nebo s touto funkcí neumíme pracovat.

Budeme hledat řešení rovnice

\[f(x)=0.\]
Budeme postupovat tak, že vyjdeme z nějaké aproximace řešení (získáme například graficky nebo zkusmo hrubou výpočetní silou) a tuto aproximaci budeme postupně zpřesňovat. Postup zpřesňování je takový, že v dosažené aproximaci funkci nahradíme lineární funkcí a další aproximace (zpřesnění předchozí aproximace) bude v nulovém bodě této lineární funkce. Za poměrně snadno splnitelných předpokladů (začneme dostatečně blízko nulového bodu a funkce má v nulovém bodě nenulovou derivaci) postup konverguje ke kořeni studované rovnice a to velmi rychle: každým krokem se přibližně zdvojnásobí počet míst, která máme správně.

Z lineární aproximace funkce \(\displaystyle f\) v bodě \(\displaystyle x_0\)

\[f(x)\approx f(x_0)+f'(x_0)(x-x_0)\]
pro \(\displaystyle x_0=x_n\), \(\displaystyle x=x_{n+1}\), \(\displaystyle f(x_{n+1})=0\) dostáváme
\[0=f(x_n)+f'(x_n)(x_{n+1}-x_n)\]
a po osamostatnění \(\displaystyle x_{n+1}\) přímo iterační vzorec
\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}.\]
Tento vzorec používáme opakovaně až do dosažení požadované přesnosti. Obvyklým testem pro ukončení výpočtu je porovnání dvou po sobě jdoucích iterací. Pokud se v rámci požadované přesnosti shodují, výpočet končí a známe přibližné řešení zadané rovnice.

Příklad. Zkusme najít číslo takové, jehož kosinus je stejný jako toto číslo. Rovnici

\[x=\cos x\]
nejprve přepíšeme do tvaru
\[x-\cos x=0\]
a hledáme vlastně řešení nulový bod funkce \(\displaystyle f(x)=x-\cos x\). Po dosazení \(\displaystyle f'(x)=1+\sin x\) získáváme iterační vzorec
\[x_{n+1}=x_n-\frac{x_n-\cos x_n}{1+\sin x_n}\]
a jednotlivé iterace s počátečním odhadem \(\displaystyle x_0=1\) a s aproximací na 60 desetinných míst dávají postupně následující hodnoty.

0.7503638678402438930349423066821768532469930658553590309665831
0.7391128909113616703605852909048902340028928367356569073234079
0.7390851333852839697601251208568043328895331231701889796312306
0.7390851332151606416617026256850263723252232625296426915134025
0.7390851332151606416553120876738734040134207763670352584051590
0.7390851332151606416553120876738734040134117589007574649656806
0.7390851332151606416553120876738734040134117589007574649656806

Vidíme, že proces opravdu neuvěřitelně rychle konverguje k řešení rovnice. Rychlost konvergence je důležitá, pokud je výpočet funkční hodnoty „drahý“. Například při modelování namáhání dřevěné konstrukce s nelineární charakteristikou aproximujeme rovnici pomocí konečných diferencí soustavou rovnic, která má desítky tisíc proměnných. Každé kolo iterační metody vyžaduje mnoho výpočtů a rychlost konvergence je zásadní.

Python skript

Úkol

2.9. Shrnutí, hlavní myšlenky#

../_images/message.jpg

Obr. 2.9 A jaká je hlavní message? Zdroj: pixabay.com#

  • Derivace udává trend ve změnách veličin a díky tomu umožňuje za určitých okolností nahrazovat komplikované funkční vztahy pomocí vztahů lineárních. Toto nazýváme lineární aproximace a je to jedna za zásadních metod, jak si inženýři zjednodušují úlohy, které by byly jinak neřešitelné.

  • Derivace dokáže detekovat růst a klesání funkce a díky tomu dokážeme také detekovat body, kde se růst zastaví a změní na klesání nebo naopak. Tyto body nás přirozeně zajímají, protože v těchto bodech je studovaná veličina maximální nebo minimální a to má dopad při minimalizaci nákladů, maximalizaci pevnosti či zisku a jiných úlohách z praktického života.

  • Pokud trend (rychlost změny, derivace) nestačí k podchycení zásadních vlastností veličiny (nastává v lokálním extrému nebo v případě, že potřebujeme lepší aproximaci, než je aproximace lineární), máme k dispozici nástroje i v tomto případě: derivace vyšších řádů a Taylorův polynom.

Obsah