9. Lineární operátory a lineární diferenciální rovnice#
Anotace.
Ukážeme si, jak se dají řešit rovnice obsahující lineární operátory, operátory, které zachovávají lineární kombinace funkcí.
Ukážeme si, že pro lineární operátory vystupující v diferenciálních rovnicích je možné najít přibližné řešení redukcí na soustavu lineárních rovnic. Toto je nejběžnější inženýrská metoda používaná při navrhování budov a staveb, při modelování proudění kapalin a plynů, při modelování přenosu tepla a dalších fyzikálních procesů.
Ukážeme si, že množina všech řešení lineární rovnice má pevnou strukturu, kterou můžeme využít k nalezení všech řešení. Pro nalezení všech řešení stačí najít jedno řešení rovnice a několik vhodných řešení rovnice jistým způsobem zjednodušení. Z těchto dílčích řešení je poté možné sestavit řešení všechna. Tím se úloha velmi zjednodušuje.
Prerekvizity.
Co se týká využitých metod studia lineárních operátorů, je přednáška relativně nezávislá. Nemá v tomto ohledu žádné prerekvizity.
Užitečnost linearity si ukážeme na příkladech diferenciálních rovnic několika typů. Proto je vhodné si zopakovat význam derivace, využití derivace v modelech založených a na diferenciálních rovnicích a interpretaci členů difuzní rovnice.
Lineární systémy je vhodné zapisovat a studovat maticově. Budeme proto potřebovat maticový součin, maticovou formulaci soustavy lineárních rovnic, nutnou a postačující podmínku jednoznačné řešitelnosti této soustavy pomocí determinantu.
Studentům obeznámeným s komplexními čísly se bude hodit Eulerova identita. Ostatní studenti budou muset příslušné pasáže akceptovat jako fakt.
9.1. Lineární operátory#
Operátorem rozumíme zobrazení, které má na vstupu i na výstupu funkci. Například pro funkce jedné proměnné mohou být operátory derivace, druhá derivace, vynásobení funkce funkcí \(\displaystyle \ln x\) anebo vnoření zadané funkce do funkce \(\displaystyle \ln x\). Tj. pro \(\displaystyle y=y(x)\) můžeme uvažovat operátory \(\displaystyle F_1[y]=\frac{\mathrm dy}{\mathrm dx}\), \(\displaystyle F_2[y]=\frac{d^2y}{dx^2}\), \(\displaystyle F_3[y](x)=y(x)\ln(x)\), \(\displaystyle F_4[y](x)=\ln(y(x)).\)

Obr. 9.1 Lineární zobrazení zachovávají některé vlastnosti. V geometrii například rovnoběžnost, v matematické analýze zachovávají lineární zobrazení lineární kombinaci. Rovnice s lineárním operátorem jsou díky tomu velmi předvídatelné. Proto je (lineární operátory i rovnice) v matematice máme tak rádi. Zdroj: pixabay.com#
Lineárním operátorem rozumíme zobrazení, které zachovává součet funkcí a násobek konstantou, tj. platí
9.1.1. Příklady lineárních operátorů#
Linearitu se naučíme využívat k tomu, abychom úlohu najít řešení rovnice rozkouskovali na řešení jednodušších úloh. Například je možné zkombinovat úlohu na stacionární proudění podzemní vody a úlohu na radiální proudění ke studni. Každou z těchto úloh umíme redukovat na separovatelnou diferenciální rovnici a vyřešit. Zkombinováním těchto úloh je možné modelovat chování studny v rovinném toku. Používá se například k zachycení kontaminace spodní vody.

Obr. 9.2 Rovinný tok podzemní vody se studnou. Podle šipek je možno určit oblast zachytáváni. Řeší se samostatně rovinný tok (kartézské souřadnice) a tok ke studni (polární souřadnice) a obě úlohy se zkombinují pomocí linearity.#
Operátor derivace, tj. operátor definovaný vztahem \(\displaystyle L[y]=\frac{\mathrm dy}{\mathrm dx}\) je lineární. Toto plyne ze vzorců pro derivaci součtu a konstantního násobku.
Buď dána funkce \(\displaystyle a(x)\). Operátor násobení funkcí \(\displaystyle a(x)\), tj. \(\displaystyle L[y](x)=a(x)y(x)\) je lineární. To plyne z komutativity násobení a z distributivního zákona (roznásobování závorek).
Složení (postupná aplikace) lineárních operátorů je lineární operátor. Například tedy
\[\frac{\mathrm d^2 y}{\mathrm dx^2}\]je lineární operátor.Součet lineárních operátorů je lineární operátor.
Buď pevně dána funkce \(\displaystyle a(x)\). Lineární operátor
\[L[y]=\frac{\mathrm dy}{\mathrm dx}+a(x)y\]se nazývá lineární diferenciální operátor prvního řádu.Buďte pevně dány funkce \(\displaystyle p(x)\) a \(\displaystyle q(x)\). Lineární operátor
\[L[y]=\frac{\mathrm d^2y}{\mathrm dx^2}+p(x)\frac{\mathrm dy}{\mathrm dx}+q(x)y\]se nazývá lineární diferenciální operátor druhého řádu.Buď dána \(\displaystyle n\times n\) matice reálných čísel \(\displaystyle A\) a \(\displaystyle n\)-vektorová funkce \(\displaystyle \vec F(x)\). Zobrazení, které funkci \(\displaystyle \vec F(x)\) přiřadí součin \(\displaystyle A\vec F(x)\) je lineární. To plyne z distributivnosti násobení vzhledem ke sčítání matic a z toho, že součin matice a reálného čísla komutuje.
Operátor z levé strany difuzní rovnice
\[ {\frac{\partial u}{\partial t}-\nabla\cdot \bigl(D\nabla u\bigr)=\sigma, }\]tj. operátor\[L[u]=\frac{\partial u}{\partial t}-\nabla\cdot \bigl(D\nabla u\bigr)\]je lineární. Po rozepsání divergence a gradientu pomocí parciálních derivací (které jsou lineární) jenom kombinujeme lineární operátory a tedy zachováváme linearitu.Rovnice podzemní vody pro proudění s napjatou hladinou
\[ {S_S\frac{\partial h}{\partial t} - \nabla\cdot \bigl(T\nabla h\bigr)= \sigma }\]je speciálním případem difuzní rovnice a operátor definovaný levou stranou je lineární. Rovnice podzemní vody pro proudění s volnou hladinou\[ {S_S\frac{\partial h}{\partial t} - \nabla\cdot \bigl(kh\nabla h\bigr)= \sigma }\]definuje operátor\[F[h]={S_S\frac{\partial h}{\partial t} - \nabla\cdot \bigl(kh\nabla h\bigr)}\]a není lineární. Pokud však využijeme rovnost\[h\frac{\partial h}{\partial x}=\frac 12 \frac{\partial h^2}{\partial x}\]a analogickou rovnost i pro další parciální derivace, je ve stacionárním případě (derivace podle času je nulová) rovnici možno přepsat do tvaru\[ - \frac 12 \nabla\cdot \bigl(k\nabla (h^2)\bigr)= \sigma \]a levá strana definuje lineární operátor v proměnné \(\displaystyle h^2\).
9.1.2. Princip superpozice#
Věta (princip superpozice)
Každý lineární operátor zachovává lineární kombinaci funkcí, tj. platí
Plyne přímo rozepsáním
9.2. Metoda konečných prvků#
Metoda konečných prvků je jedna z nejběžnějších numerických metod pro řešení diferenciálních rovnic v inženýrských aplikacích. Ukážeme si základní myšlenky této metody na jednoduchém příkladu rovnice
9.2.1. Slabá formulace#
Nejprve převedeme rovnici na tzv. slabou formulaci. To je formulace, kde nevystupuje druhá derivace funkce \(\displaystyle u\), ale jenom derivace první. To umožní pracovat například s úlohami vedení tepla, kde se materiálové vlastnosti mění skokem. Kromě toho slabá formulace převádí úlohu na úlohu integrální, což je výhodné pro numerické metody. Na tuto výhodu se zaměříme a proto nebudeme rozebírat aspekty spojené s hladkostí funkcí. Budeme předpokládat, že funkce, se kterými pracujeme, jsou dostatečně hladké.
Použijeme základní poznatky z integrálního počtu a derivaci součinu funkcí \(\displaystyle u'\) a \(\displaystyle v\)
Nyní přistoupíme k převodu rovnice (E) na obecnější formulaci. Rovnici napíšeme pro jednoduchost s derivacemi vyjádřenými čárkami a s vynechanou závislostí na \(\displaystyle x\)
9.2.2. Galerkinova metoda#
Vyjdeme ze slabé variační formulace (W) a budeme hledat přibližné řešení ve tvaru
Derivace funkce \(\displaystyle u(x)\) je
Galerkinova metoda spočívá v tom, že za funkci \(\displaystyle v(x)\) volíme postupně jednotlivé bázové funkce, tedy \(\displaystyle v(x)=\varphi_i(x)\) pro \(\displaystyle i=1,2,\ldots,n\). Tím dostaneme soustavu rovnic

Obr. 9.3 Bázové funkce pro metodu konečných prvků na intervalu [0,1] s dělením na deset dílčích intervalů. V obrázku jsou vybrány tři bázové funkce a lineární kombinace bázových funkcí aproximující parabolu \(\displaystyle y=2x(1-x)\).#
Je účelné volit bázové funkce tak, aby na jednu stranu generovaly dostatečně širokou škálu funkcí, ale také aby byla matice \(\displaystyle A\) vhodná pro numerické řešení — například, aby byla řídká. Vhodnou volbou jsou trojúhelníkové funkce dle připojeného obrázku. Pomocí lineární kombinace těchto funkcí je možné vyjádřit libovolnou po částech lomenou funkci splňující nulové okrajové podmínky. Při takto zvolených funkcích je \(\displaystyle a_{ij}\) nulové, pokud se \(\displaystyle i\) a \(\displaystyle j\) liší více než o jedničku a matice \(\displaystyle A\) má nenulové prvky jenom na hlavní diagonále a na dvou přilehlých diagonálách (je tridiagonální). Výpočet integrálů pro \(\displaystyle a_{ij}\) vede k následující matici.
9.2.3. Metoda konečných prvků (FEM)#

Obr. 9.4 Ukázka programu pro modelování pomocí metody konečných prvků (FEM). V tomto případě je modelován tříbodově podepřený nosník zatížený silou uprostřed. Program umožňuje měnit parametry nosníku a zatížení a okamžitě vidět výsledky a identifikovat kritická místa konstrukce.#
Výše uvedený postup tvoří jádro metody konečných prvků (angl. finite element method, FEM). Problém je nejprve naformulován obecněji než v původní diferenciální rovnici (slabá variační formulace) a poté je hledáno přibližné řešení v podprostoru generovaném zvolenými bázovými funkcemi. Dosazením tohoto tvaru řešení do slabé formulace a volbou testovacích funkcí je získána soustava lineárních rovnic pro neznámé koeficienty v rozvoji řešení podle bázových funkcí. Tuto soustavu je poté možné vyřešit běžnými numerickými metodami pro řešení soustav lineárních rovnic.
Uvedený postup je možné zobecnit na složitější rovnice a úlohy. Na rozdíl od analytických metod si metoda konečných poradí i s komplikovanějšími geometrickými tvary a nespojitými materiálovými vlastnostmi, kdy na sebe navazují dva odlišné materiály. Je možné metodu použít i pro nelineární rovnice, i když v tomto případě je výpočet numericky náročnější.
Výhodou metody konečných prvků oproti metodě konečných diferencí je větší volnost diskretizaci. Metoda konečných diferencí vyžaduje pravidelnou síť bodů, kdežto metoda konečných prvků umožňuje využít nepravidelnou síť a přizpůsobit hustotu bodů místním potřebám. To je výhodné například při zjemnění diskretizace v místech, kde se očekávají velké změny řešení.
Poznámka.
Metodu podrobněji rozebereme a zařadíme do širšího kontextu numerických metod při studiu numerických metod pro parciální diferenciální rovnice v poslední přednášce semestru.
9.3. Řešení pomocí principu superpozice#
Mějme rovnici
Například pro \(\displaystyle b(t)=0\) a \(\displaystyle L[x]=\frac{\mathrm dx}{\mathrm dt}-x\) má rovnice tvar
\[\frac{\mathrm dx}{\mathrm dt}-x=0,\]tj.\[\frac{\mathrm dx}{\mathrm dt}=x.\]
Následující věta vlastně vyjadřuje totéž co princip superpozice z předchozího textu, pouze v jiných pojmech: v pojmech řešení rovnice s lineárním operátorem.
Věta (princip superpozice při řešení rovnic)
Jsou-li funkce \(\displaystyle x_1(t)\) a \(\displaystyle x_2(t)\) po řadě řešeními rovnic
Pro \(\displaystyle b_1(t)=b_2(t)=0\) všechny tři výše uvedené rovnice splynou a lineární kombinace dvou řešení homogenní lineární rovnice je také řešením. Toto je možné pochopitelně rozšířit na libovolný konečný počet funkcí.
Pro \(\displaystyle b_1(t)=0\) a \(\displaystyle C_2=1\) jsou obě nehomogenní rovnice stejné a pokud k řešení rovnice přičteme řešení asociované homogenní rovnice (se stejným operátorem na levé straně, ale nulou na pravé straně), dostaneme řešení stejné rovnice.
Z těchto jednoduchých tvrzení plyne několik zásadních pozorování.
Pokud máme k dispozici několik řešení homogenní rovnice, libovolná jejich lineární kombinace je také řešením.
Za určitých okolností lineární kombinace z předchozího bodu umožní splnit libovolnou počáteční podmínku a vzhledem k jednoznačnosti řešení, která lineární rovnice zpravidla provází, je jistota, že žádné další řešení neexistuje. Nalezení těchto funkcí je tedy zásadní krok při řešení rovnice.
U nehomogenní rovnice se úloha najít všechna řešení dá rozdělit na dvě dílčí úlohy: najít jenom jedno řešení a k tomu najít všechna řešení homogenní rovnice se stejnou levou stranou. Každá z těchto dvou úloh je mnohem lehčí než úloha celková a součtem jednoho řešení nehomogenní rovnice a obecného řešení asociované homogenní rovnice dostaneme obecné řešení nehomogenní rovnice.
9.3.1. Příklad využití linearity v jedné dimenzi#
Pro konkrétnost specifikujeme myšlenky z předchozího textu na příkladě.
Pro jednu funkci lineární kombinace degenerují na násobky. Proto je obecné řešení rovnice součtem jednoho řešení rovnice a obecného řešení asociované homogenní rovnice. Toto jedno řešení vlastně udává pozici v prostoru funkcí a řešení asociované homogenní rovnice udává směr. Například funkce \(\displaystyle x=e^t\) splňuje rovnici
9.4. Lineární diferenciální rovnice prvního řádu s konstantními koeficienty#
V aplikacích často vídáme rovnici tvaru
která vznikne například úpravou rovnice
Podobně jako v předchozím příkladě stačí najít jedno řešení rovnice (9.1) a jedno nenulové řešení rovnice
První z řešení udává bod v prostoru funkcí, druhé řešení jakýsi směr a společně definují jakousi přímku obsahující všechna řešení. Rovnici (9.1) splňuje konstantní funkce \(\displaystyle x(t)=\frac ba\) a rovnici (9.2) exponenciální funkce \(\displaystyle x(t)=e^{-at}.\) Obecné řešení rovnice (9.1) je proto
Věta (řešení lineární diferenciální rovnice prvního řádu s konstantními koeficienty)
Obecným řešením rovnice
Obrat, že stacionární řešení je globálně atraktivní znamená, že všechna řešení k tomuto stacionárním stavu konvergují nezávisle na počáteční podmínce.
9.4.1. Další lineární rovnice#
Pro skalární lineární diferenciální rovnice druhého řádu je situace
obdobná, pouze pro řešení asociované homogenní diferenciální rovnice
potřebujeme dvě lineárně nezávislá řešení (jedno není násobkem druhého).
Například \(\displaystyle x_1(t)=e^t\) a \(\displaystyle x_2(t)=e^{-t}\) nejsou jedno násobkem druhého a obě splňují rovnici
9.5. Lineární autonomní systémy#
Pokud pracujeme s nekonstantními vektorovými funkcemi tak, že při derivaci derivujeme každou komponentu samostatně, je rovnice
9.5.1. Lineární autonomní systém ve dvou dimenzích#
Následující příklad je mírně modifikovaný příklad z kurzu MIT o diferenciálních rovnicích. Ve formulaci s vařením vajíčka se zdá triviální a prakticky neužitečný. Toto je však voleno pro jednoduchost výkladu a snadnou představu povahy zkoumaného jevu. V praxi se stejným modelem předává teplo vrstveným materiálem (jako je tepelná ochrana domů nebo raketoplánů) nebo chemické látky vstupující do dalších reakcí (jako například řetěz reakcí vedoucí k syntéze bílkovin, které buňka v reakci na okolní prostředí potřebuje k přežití).

Obr. 9.5 Vajíčko je vhodný model pro zprostředkování přenosu tepla a tím i pro popis změny teploty pomocí systému dvou diferenciálních rovnic. Zdroj: pixabay.com#
Budeme modelovat ohřívání vejce ve vodě o konstantní teplotě \(\displaystyle T_0\). Na počátku mají bílek a žloutek teplotu \(\displaystyle T_1\) a \(\displaystyle T_2\). Žloutek přebírá teplo od bílku rychlostí úměrnou rozdílu teplot žloutku a bílku. Bílek přebírá teplo od vodní lázně rychlostí úměrnou rozdílu teplot a předává teplo žloutku procesem popsaným v předchozí větě. Vody je hodně a její teplota se nemění. Proces můžeme modelovat soustavou diferenciálních rovnic
tj. symbolicky \(\displaystyle X'=AX\), kde \(\displaystyle X=(T_1,T_2)^T\) je vektorová funkce (sloupcový vektor) a \(\displaystyle A\) je \(\displaystyle 2\times 2\) matice.
9.5.2. Systém \(\displaystyle X'=AX\)#
Je-li determinant matice nenulový, má soustava \(\displaystyle AX=0\) pouze nulové řešení a systém
má jediné konstantní řešení, kterým je počátek. Konstantní řešení bude nazývat stacionární bod.
Tento systém můžeme přepsat na
Je možné ukázat, že každá počáteční úloha je jednoznačně řešitelná a pro obecné řešení stačí najít tolik nezávislých řešení, kolik komponent má neznámá vektorová funkce \(\displaystyle X\). Platí následující věta, kterou je možno ověřit přímo dosazením.
Věta (souvislost vlastních čísel matice a řešení lineárního autonomního systému)
Má-li matice \(\displaystyle A\) vlastní číslo \(\displaystyle \lambda\) a příslušný vlastní vektor je \(\displaystyle v\), tj. platí \(\displaystyle A v =\lambda v\), je funkce \(\displaystyle X(t)=v e^{\lambda t}\) řešením systému \(\displaystyle X'=AX.\) Jsou-li \(\displaystyle \lambda\) a \(\displaystyle v\) komplexní, je řešením i samostatně reálná část a imaginární část.
Systém
je možno na tvar (9.4) převést po přepsání do tvaru \(\displaystyle (X-X_0)'=A(X-X_0)\), kde \(\displaystyle X_0\) je řešením soustavy \(\displaystyle AX+B=0\), což odpovídá posunu stacionárního bodu do počátku.
Poznámka (vlastní hodnoty a řešení)
Následující poznatky jsou shrnutím a specifikací výše uvedeného a klasifikují stabilitu některých řešení systému (9.5), tj.
Jakmile má matice \(\displaystyle A\) reálnou kladnou vlastní hodnotu, existuje řešení, které se vzdaluje od stacionárního bodu směrem daným příslušným vlastním vektorem.
Jakmile má matice \(\displaystyle A\) reálnou zápornou vlastní hodnotu, existuje řešení, které se přibližuje ke stacionárnímu bodu ze směru daného příslušným vlastním vektorem.
Jakmile má matice \(\displaystyle A\) komplexní hodnotu s kladnou reálnou částí, existuje řešení, které se v oscilacích vzdaluje od stacionárního bodu.
Jakmile má matice \(\displaystyle A\) komplexní hodnotu se zápornou reálnou částí, existuje řešení, které se v oscilacích přibližuje ke stacionárnímu bodu.
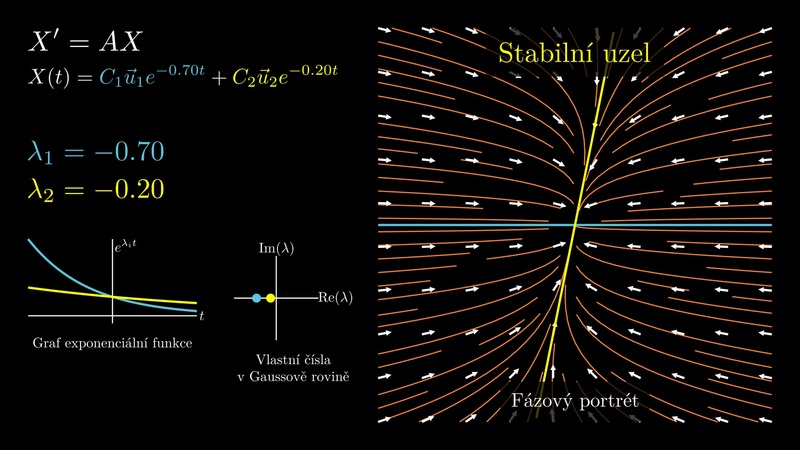
Pokud jsou například všechna vlastní čísla v daném bodě záporná, poté každé z nich generuje řešení konvergující do stacionárního bodu. Díky linearitě, jednoznačnosti řešení a tomu, že máme tolik řešení, kolik je nutno pro splnění libovolné podmínky, je možné pomocí těchto dílčích řešení zapsat i libovolné jiné řešení. Tím pádem ale všechna řešení konvergují do stacionárního bodu. Pokud jsou vlastní čísla komplexní se zápornou reálnou částí, je situace stejná, ale řešení navíc konvergují do stacionárního bodu postupnými oscilacemi. Podobně, pokud všechny vlastní hodnoty jsou kladné, všechna řešení se od stacionárního bodu vzdalují a pokud jsou všechny vlastní hodnoty komplexní s kladnou reálnou částí, probíhá toto vzdalování oscilacemi s narůstající amplitudou.

Obr. 9.6 Podobný model jako ohřívání vajíčka je možno použít pro transport látek mezi krví a orgány. Zdroj: pixabay.com, 10918156#
Příklad. Model ohřívání vajíčka (9.3) z předchozí části této přednášky má (v posunuté teplotní stupnici, na které teplota varu vody odpovídá nule) stacionární bod \(\displaystyle (0,0)\). Zkusíme zvolit parametry \(\displaystyle k_1\) a \(\displaystyle k_2\) a určit chování trajektorií v okolí tohoto bodu. Pro \(\displaystyle k_1=1\) a \(\displaystyle k_2=2\) dostáváme
9.6. Mechanický oscilátor#

Obr. 9.7 Příklad mechanického oscilátoru Zdroj: pixabay.com, Couleur#

Obr. 9.8 Kmity kmene stromu. Jejich analýza pomáhá k pochopení stability stromů ve větru. Zdroj: projekt DYNATREE#
S mechanickým oscilátorem se setkáváme tam, kde je systém vychýlen z rovnovážné polohy a nějaká síla jej do této rovnovážné polohy vrací. Přičemž v některých situacích dojde (například vlivem setrvačnosti) k tomu, že systém se přehoupne přes rovnovážnou polohu na opačnou stranu a vrací se zpět. Klasickým případem je těleso o hmotnosti \(\displaystyle m\) na pružině. Pokud sílu závisející na rychlosti \(\displaystyle v\) a výchylce \(\displaystyle x\) označíme \(\displaystyle F\), dostáváme
Poznámka (diferenciální rovnice druhého řádu)
Uvažovaný systém se v literatuře často vyskytuje ve tvaru, kdy je rychlost \(\displaystyle v\) dosazena do druhé rovnice a poté dostáváme model ve tvaru